Usuari:Jordiventura96/proves/Arrel quadrada de 3

Valor de l'arrel de 3 $({\sqrt {3}})$
Decimal	1.7320508075688772935...
Binari	1.1011101101100111101...
Hexadecimal	1.BB67AE8584CAA73B....
Fracció contínua	$1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{\ddots }}}}}}}}}}$
Forma algebraica	${\sqrt {3}}$

L'arrel quadrada de 3 és l'únic nombre positiu que multiplicat per si mateix dóna 3. Es denota com ${\sqrt {3}}$. El seu valor numèric amb deu xifres decimals és:

${\sqrt {3}}\approx 1,7320508075\dots$

L'arrel quadrada de 3 és un nombre irracional. També es coneix com la constant de Teodor, en honor al filòsof grec Teodor de Cirene.

Geometria

Un triangle equilàter de costat 2 té una altura igual a ${\sqrt {3}}$

L'arrel quadrada de tres és igual a la longitud entre dos costats paral·lels d'un hexàgon de costat la unitat.

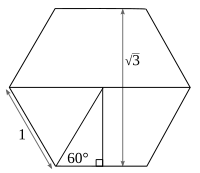
Si es té un triangle equilàter de costat la unitat, i es traça una bisectriu qualsevol, s'obtenen dos triangles que tenen com a hipotenusa 1, i els catets de 1/2 i √3/2 respectivament. D'aquí es té que la tangent de l'angle de 60º (o π/3) sigui igual a l'arrel de 3.

Aquesta és també la distància entre els dos costats paral·lels d'un hexàgon regular de costat la unitat, com es mostra en el dibuix.

L'arrel de 3 també és igual a la diagonal interior d'un cub els costats del qual tinguin com a mesura la unitat. Això pot ser demostrat mitjançant el teorema de Pitàgores de la següent manera:

Com que els costats d'una de les bases del cub també formen triangles rectangles, llavors podem obtenir la mesura de la diagonal de la cara mitjançant el teorema de Pitàgores:

$1^{2}+1^{2}=d^{2}\,\!$;

$d={\sqrt {2}}$

Ara considerarem el triangle que té com a catets la diagonal de la cara i una aresta del cub. La hipotenusa d'aquest triangle rectangle serà la diagonal interna del cub. El seu valor també el podrem conèixer mitjançant el teorema de Pitàgores.

$1^{2}+({\sqrt {2}})^{2}=x^{2}$;

$x={\sqrt {3}}$

Quedant, doncs demostrat que la diagonal interior d'un cub que té la unitat com a mesura de l'aresta, és igual a l'arrel quadrada de 3.

Trigonometria

De manera natural sorgeix l'arrel quadrada de 3 en el sinus de l'angle de 60º; i complementàriament en el cosinus de 30º. També usant la circumferència goniomètrica apareix l'arrel quadrada de 3 en definir el sinus i el cosinus de 120º i 240º. A més, en el pla complex les arrels cúbiques complexes d'1 també comporten l'arrel de 3.

Irracionalitat

La irracionalitat de l'arrel quadrada de 3 es pot demostrar mitjançant un argument semblant al que s'utilitza per demostrar la irracionalitat de l'arrel quadrada de dos. Es fonamenta en la reducció a l'absurd.

Es parteix de la hipòtesi que l'arrel de 3 és un nombre racional, i que per tant es compleix que:

${\sqrt {3}}={\frac {p}{q}}\quad \rightarrow \quad 3={\frac {p^{2}}{q^{2}}}\quad \rightarrow \quad 3q^{2}=p^{2}$

essent p i q nombres primers entre ells. Llavors, si p² és múltiple de 3, també p ho ha de ser, per tant:

$p=3r\quad \rightarrow \quad 3q^{2}=9r^{2}\quad \rightarrow \quad q^{2}=3r^{2}$

i per tant, es té que també q és múltiple de 3, fet que contradiu la premissa principal segons la qual p i q eren primers entre ells.

Enllaços externs

• Provar que l'arrel quadrada de 3 és irracional (en inglés)
• Weisstein, Eric W., «Constante de Theodorus» a MathWorld (en anglès).

Vegeu també

• Arrel quadrada
• Arrel quadrada de 2