Usuari:Mcapdevila/Torus De Bruijn
 | Aquest article tenia importants deficiències de traducció i ha estat traslladat a l'espai d'usuari. Podeu millorar-lo i traslladar-lo altra vegada a l'espai principal quan s'hagin resolt aquestes mancances. Col·laboreu-hi! |
|
|

En combinatorial matemàtiques, un De Bruijn torus, va anomenar després de Nicolaas Govert de Bruijn, és una varietat de símbols d'un alfabet (sovint només 0 i 1) que conté cada m-per-n matriu exactament una vegada que. És un torus perquè les vores són considerades wraparound pel propòsit de trobar matrius. El seu nom ve del De Bruijn seqüència, els quals poden ser considerats un cas especial on n és 1 (una dimensió).
Un de les qüestions obertes principals pel que fa a De Bruijn tori és si un De Bruijn torus per una mida d'alfabet particular pot ser construïda per un donat m i n. És sabut que aquests sempre existeixen quan n = 1, des de llavors senzillament aconseguim el De Bruijn seqüències, el qual sempre existeix. És també sabut que "quadrat" tori existir quan sigui que m = n i fins i tot (pel cas estrany el resultant tori no pot ser quadrat).[1][2][3]
La plaça binària "possible més petita" de Bruijn torus, va descriure per sobre de correcte, va denotar mentre (4,4;2,2)2 de Bruijn torus (o senzillament tan B2), conté tot 2×2 matrius binàries.
B2
[modifica]A part de "traducció", "inversion" (intercanviant 0s i 1s) i "rotació" (per 90 graus), no altre (4,4;2,2)2 de Bruijn tori és possible - això pot ser mostrat per inspecció completa de tot 216 matrius binàries (o el subconjunt que compleix constreny com números iguals de 0s i 1s) .[4]
Exemple més gran: B4
[modifica]Un exemple de la plaça binària "possible pròxima" de Bruijn torus, (256,256;4,4)2 (abreujat tan B4), ha estat explícitament va construir.[5]
La imatge sota espectacles un exemple d'un (256,256;4,4)2 de Bruijn torus / varietat, on el zeroes ha estat codificat tan negre i los píxels tan blancs respectivament.
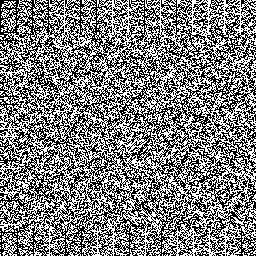
Consideració pràctica per construcció de de Bruijn tori B6 & B8
[modifica]El paper en quin un exemple del (256,256;4,4)2 de Bruijn torus / la varietat era va construir contingut per damunt 10 pàgines van omplir essencialment només amb 0s i 1s, fins i tot encara que la mida de font era va reduir comparat amb el text principal, cada fila de la varietat va imprimir per damunt 3 línies.
La plaça binària "possible subsegüent" de Bruijn torus, contenint tot binari 6×6 matrius, tindria 236 = 68,719,476,736 entrades, cedint una varietat quadrada de dimensió 262,144x262,144, això seria denotat un (262144,262144;6,6)2 de Bruijn torus / varietat o senzillament tan B6. Hagi de ser possible de construir un exemple, el qual cabria a un moderar ordinador (imprimint-lo fora on cada entrada seria representada per un píxel de mida 0.1 mm requeriria una àrea de approx 26×26 [metre quadrat]s).
L'objecte B8, contenint tot binari 8×8 matrius, amb un total de 264 = 18,446,744,073,709,551,616 entrades, denotat (4294967296,4294967296;8,8)2 és actualment massa gran per fins i tot un supercomputer, requerint d'ordre 18 Exabytes, a fora d'un 64-va mossegar espai d'adreça (assumint 1 byte d'emmagatzematge per cada element, dins teoria només 1 bit seria suficient per cada element, només d'ordre 2 Exabytes seria requerit, el qual és encara 3 ordres de la magnitud més gran que emmagatzematge de memòria / total d'alguns dels ordinadors més grans mentre de tardà 2013).
Veu també
[modifica]- Seqüència De Bruijn
- Graf De Bruijn
Referències
[modifica]- ↑ «On de Bruijn arrays.». Ars Combinatoria A, 19, 1985, pàg. 205–213.
- ↑ «Universal cycles for combinatorial structures.». Discrete Mathematics, 110, 1, 1992, pàg. 43–59. DOI: 10.1016/0012-365x(92)90699-g.
- ↑ ; Stevens, Brett; Hurlbert, Glenn «Research problems on Gray codes and universal cycles». Discrete Mathematics, 309, 17, 9-2009, pàg. 5341–5348. DOI: 10.1016/j.disc.2009.04.002.
- ↑ Falta indicar la publicació .
- ↑ Falta indicar la publicació .
