Usuari:Mcapdevila/Trencaclosques del quadrat fantasma
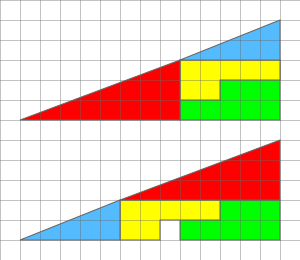
El trencaclosques del quadrat fantasma es basa en una il·lusió òptica i se sol emprar a les classes de matemàtiques per a estimular en els alumnes el raonament sobre la geometria plana. Consisteix en completar un trencaclosques disposant les peces de dues maneres diferents però arribant a la mateixa figura final. La sorpresa és que en una de les dues figures que s'obtenen hi ha un forat, de forma generalment quadrada. Hi ha diferents trencaclosques que s'ajusten a aquesta descripció; el més conegut és el del triangle rectangle de 13x5 que mostra la figura. En la primera disposició el triangle té una àrea de 32,5 quadrats (13×5/2 = 65/2 = 32,5) i en la segona –sorprenentment– n'hi ha un menys, per tant 31,5 quadrats. Si, en canvi, el càlcul de l'àrea es fa sumant els quadrats de cada peça:
- Verda : 8 quadrats
- Groga : 7 quadrats
- Blava : 5 quadrats (superfície d'un triangle rectangle =5x2/2)
- Roja : 12 quadrats (8x3/2)
resulta un triangle d'àrea 8 + 7 + 5 + 12 = 32 quadrats.
Explicació
[modifica]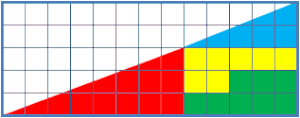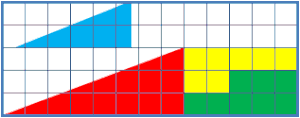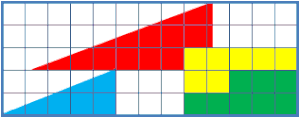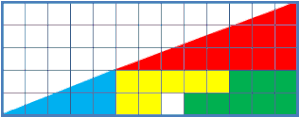
La clau és que cap dels dos triangles de 13x5 és un autèntic triangle perquè, encara que a simple vista sembla una línia recta, la hipotenusa està formada en tots dos casos per dos segments que no tenen el mateix pendent: les hipotenuses dels dos triangles petits. Els pendents de les hipotenuses dels triangles són: triangle roig: 3/8 = 0,375; triangle gran: 5/13 = 0,385; triangle blau: 2/5 = 0,400. Són inclinacions prou similars per a que l'ull poc atent no les distingeixi.
Segons Martin Gardner, un conegut divulgador científic en el món anglosaxó, aquest trencaclosques el va inventar Paul Curry, un mag aficionat de Nova York, l'any 1953. Això no obstant, el principi en el qual es fonamenta era conegut des de començaments del segle XVI.
Les dimensions de les peces d'aquest trencaclosques (els enters 2, 3, 5, 8, 13) són números de Fibonacci consecutius. Hi ha molts puzzles de dissecció geomètrica que es basen també en propietats de la seqüència de Fibonacci.
Trencaclosques similars
[modifica]

Basant-se en la idea del triangle descrit s'han creat extraordinaris números de prestidigitació.[1]
Un altre trencaclosques del mateix tipus (il·lustrat en la figura animada de l'esquerra) fa servir quatre quadrilàters “congruents” que formen un quadrat més gran. Les peces es poden disposar de dues maneres diferents per a formar dos quadrats en aparença de la mateixa mida, però un d'ells té un petit forat quadrat al centre. L'explicació de la paradoxa és que el costat del segon quadrat és una mica més llarg que el del primer. La diferència entre ambdós costats depèn de quan s'allunyen dels 90º els angles del vèrtex de les quatre peces del trencaclosques. Es demostra que la relació entre el costat del quadrat en les dues situacions és igual al cosinus dels angles esmentats. Per exemple, si aquests angles es desvien 5º de l'angle recte, la relació entre els costats és 1,0038, és a dir, 0,4%, una variació imperceptible.
La descomposició de la dreta, on un quadrat d'àrea 64 es converteix en un rectangle d'àrea 65, la va idear Sam Loyd[2]; aquí l'explicació de la paradoxa rau en que els costats de les peces no són exactament iguals, i per això deixen buit un fi paral·lelogram d'àrea 1 al centre del rectangle. Reblant el clau, una segona transformació del quadrat el converteix en una figura d'àrea 63.
Referències
[modifica]- ↑ «Els quadrats escapistes» (en anglès). [Consulta: 25 maig 2013].
- ↑ O més aviat el seu fill, segons Martin Gardner; tot i que podria ser anterior; veure Sam Loyd's son's dissection (anglès).
Enllaços externs
[modifica]- Curry's Paradox: How Is It Possible? a cut-the-knot (anglès)
- Gianni A. Sarcone Magic Triangles, or the Area Paradox a httpp://www.archimedes-lab.org (anglès)
