Velocitat de la llum
 En aquesta imatge, una llum làser es mou per l'aire al 99,97% de la velocitat de la llum en el buit. | |
| Valors exactes | |
|---|---|
| Metres per segon | 299.792.458 |
| Longitud de Planck per temps de Planck (és a dir, unitats de Planck) | 1 |
| Valors aproximats | |
| Quilòmetres per segon | 300.000 |
| Quilòmetres per hora | 1.080 milions |
| Unitats astronòmiques per dia | 173 |
| Temps aproximat que triga la llum en recórrer... | |
| un centímetre | 33 ps |
| un metre | 3,3 ns |
| un quilòmetre | 3,3 μs |
| una milla | 5,4 μs |
| al voltant de l'equador de la Terra | 0,13 s |
| de la Terra a òrbita geoestacionària i de tornada | 0,24 s |
| de la Terra a la Lluna | 1,3 s |
| de la Terra al Sol | 8,3 min |
| de la Terra a Alpha Centauri | 4,4 anys |
| d'un extrem a l'altre de la Via Làctia | 100.000 anys |
La velocitat de la llum en el buit, comunament representada amb la lletra c, és una constant física universal important en molts camps de la física. El seu valor és exactament 299 792 458 metres per segon, un valor exacte perquè la longitud del metre es defineix a partir d'aquesta constant i la definició estàndard internacional de segon.[1] D'acord amb la relativitat especial, c és la velocitat màxima a la qual pot viatjar tota l'energia, la matèria i la informació de l'Univers. És la velocitat a la qual totes les partícules sense massa i els seus camps associats (inclosa la radiació electromagnètica, com la llum) viatgen en el buit. És també la velocitat de la gravetat (és a dir, de les ones gravitatòries) predita per les teories actuals. Aquestes partícules i ones viatgen a c, independentment del moviment de la font o el sistema de referència inercial de l'observador. En la teoria de la relativitat, c interrelaciona l'espai i el temps, i també apareix en la famosa equació d'equivalència massa-energia, E = mc².[2]
La velocitat a la qual la llum es propaga a través de materials transparents, com el vidre o l'aire, és menor que c. La relació entre c i la velocitat v a la qual viatja la llum a través d'un material s'anomena l'índex de refracció n del material (n = c / v). Per exemple, l'índex de refracció del vidre per la llum visible és típicament d'aproximadament 1,5, cosa que significa que la llum en el vidre viatja a c / 1,5 ≈ 200 000 km/s; l'índex de refracció de l'aire per la llum visible és d'1,000 293, de manera que la velocitat de la llum en l'aire és de 299 705 km/s (prop de 88 km/s més lenta que c).
Velocitat finita
[modifica]Ole Rømer va demostrar per primera vegada el 1676 que la llum viatja a una velocitat finita (a diferència de fer-ho de manera instantània) en estudiar el moviment aparent de la lluna de Júpiter Io. El 1865, James Clerk Maxwell va proposar que la llum era una ona electromagnètica, i que per tant viatjava a la velocitat c que apareix en la seva teoria de l'electromagnetisme.[3] El 1905, Albert Einstein va postular que la velocitat de la llum respecte qualsevol sistema inercial és independent del moviment de la font de llum,[4] i va explorar les conseqüències d'aquest postulat en la teoria especial de la relativitat i va mostrar que el paràmetre c tenia rellevància fora del context de la llum i l'electromagnetisme. Després de segles de mesures cada vegada més precises, el 1975 es va trobar que la velocitat de la llum era de 299 792 458 m/s, amb una incertesa de mesura de 4 parts per mil milions. El 1983, el metre va ser redefinit en el sistema internacional d'unitats (SI) com la distància recorreguda per la llum en el buit en 1/299 792 458 segons. Com a resultat, el valor numèric de c en metres per segon queda actualment fixat exactament per la definició del metre.[5]
En alguns casos es pot considerar, de manera aproximada, que la llum i altres ones electromagnètiques es mouen «instantàniament», però la velocitat finita de la llum té efectes considerables per a llargues distàncies i mesures molt sensibles. Per exemple, en la comunicació amb sondes espacials llunyanes, un missatge pot trigar un temps mensurable en hores o minuts a anar des de la Terra fins a la sonda, afectant les condicions de recepció i emissió. En altres casos, la seva mensurabilitat pot ser qüestió d'anys o segles, com ara la llum de les estrelles llunyanes, que veiem molts anys després que l'estrella desapareixés, cosa que permet estudiar la història de l'Univers mitjançant l'observació d'objectes distants. La velocitat finita de la llum també limita la velocitat màxima teòrica dels ordinadors, ja que la informació ha de ser enviada dins de l'ordinador d'un xip a un altre. La velocitat finita de la llum també es pot utilitzar en mesures de temps de vol per a mesurar grans distàncies amb una alta precisió.
Notació i unitats
[modifica]Normalment es fa servir el símbol c, de "constant" o del llatí celeritas ('rapidesa') per a denotar la velocitat de la llum en el buit.[6] Originàriament, es feia servir el símbol V per a la velocitat de la llum, introduït per James Clerk Maxwell el 1865. El 1856, Wilhelm Eduard Weber i Rudolf Kohlrausch havien usat c per a una constant diferent que en el futur es mostraria ser igual a vegades la velocitat de la llum en el buit. El 1894, Paul Drude va redefinir c en el seu significat modern. El 1905, Einstein va utilitzar V en els seus articles originals en alemany sobre la relativitat especial, però el 1907 es va passar a c, que llavors s'havia convertit ja en el símbol estàndard.[7][8]
De vegades, c es fa servir per a la velocitat de les ones en qualsevol medi, i c0 per a la velocitat de la llum en el buit.[9] Aquesta notació en què es fa servir el subíndex, recolzada en la documentació oficial del SI,[5] té la mateixa forma que altres constants relacionades: μ0 per a la permeabilitat del buit o constant magnètica, ε0 per a la permitivitat del buit o constant elèctrica, i Z0 per a la impedància característica del buit. En aquest article, es fa servir c exclusivament per a la velocitat de la llum en el buit.
Des de 1983, el metre s'ha definit en el SI com la distància que la llum recorre en el buit en 1/299 792 458 parts de segon. Aquesta definició fixa la velocitat de la llum en el buit en exactament 299 792 458 m/s.[10][11][12] Com una constant física dimensional, el valor numèric de c és diferent per a diferents sistemes d'unitats. En les branques de la física en què c apareix sovint, com ara la relativitat, és comú l'ús dels sistemes d'unitats naturals de mesura o el sistema d'unitats geometritzat, en què c=1.[13][14] Amb l'ús d'aquestes unitats, c no apareix explícitament perquè la multiplicació o divisió per 1 no n'afecta el resultat.
Descripció
[modifica]La llum és un tipus de radiació electromagnètica. Segons la teoria electromagnètica, totes les radiacions electromagnètiques es desplacen per l'espai lliure a la velocitat de la llum en espai lliure: 299 792 458 m/s. Aquesta definició és aplicable sense importar el color, la intensitat, la font o la direcció de la llum. Alguns exemples de medis reals que s'acosten al buit ideal són l'espai exterior, el medi interestel·lar, el medi interplanetari, el buit quàntic, el buit de QCD i l'ultrabuit. Dins del marge d'error experimental, no s'han trobat variacions en la velocitat de llum en cap d'aquests medis realitzables, de manera que el seu comportament s'aproxima bé al de l'espai lliure. A més, les observacions mostren que la variació de la velocitat de la llum a mesura que l'univers envelleix és de menys de dues parts en 10¹⁶/any, tant per a les microones com per a la llum visible.
Segons la relativitat especial, la velocitat de la llum té el mateix valor en tots els sistemes de referència inercials. La freqüència observada pot diferir entre dos observadors amb velocitats diferents, causant un fenomen conegut com a efecte Doppler.
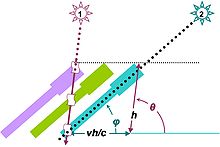
Efecte pràctic de la velocitat finita de la llum
[modifica]La velocitat de la llum té un paper important en moltes ciències i tecnologies actuals. Els sistemes de radar amiden la distància a un objectiu mesurant el temps que triga un eco del pols de llum a retornar-ne. De manera similar, un sistema de posicionament global (GPS) mesura la seva distància a satèl·lits basant-se en quant triga a arribar del satèl·lit un senyal de ràdio. Les distàncies a la Lluna, a planetes i a sondes espacials són determinades mesurant el temps que triga la llum a anar-hi i tornar-ne.
Un altre efecte de la velocitat finita de la llum és l'aberració estel·lar. Imaginant que s'observa un estel amb un telescopi idealitzat com un tub estret, la llum entra al tub provinent de l'estel amb un angle θ i viatja a la velocitat c, tarda un temps h/c" per arribar al fons del tub, on l'ull detecta la llum. Suposant que les observacions es fan des de la Terra, que es mou a una velocitat v, durant el trànsit de la llum, el tub es mou a una distància vh/c. Per consegüent, perquè el fotó arribi al fons del tub, aquest ha d'estar inclinat un angle φ, diferent de θ, i en resulta una posició aparent de l'estel a l'angle φ.
En astronomia, més enllà del sistema solar, les distàncies sovint es mesuren en anys llum, la distància que recorre la llum en un any.
En sistemes electrònics, malgrat la seva mida reduïda, la velocitat de la llum pot ser un factor limitant en la seva velocitat d'operació màxima.[15][16]
Mesures de la velocitat de la llum
[modifica]Abans del segle xvii, la comunitat científica creia que la velocitat de la llum no era finita, sinó que es movia de manera instantània. Prèviament, en el segle xiii, Roger Bacon ja advertí d'una velocitat de llum finita; això no obstant, va afirmar que era tan alta, que no es podria mesurar mai. L'any 1676, l'astrònom Ole Rømer va detectar unes desigualtats entre un satèl·lit de Júpiter i l'ombra que produïa sobre el planeta, i arribà a la conclusió final que la llum no podia presentar una velocitat infinita. Els càlculs del deixeble de Røemer s'acostaren bastant a la veritable velocitat de la llum.
No fou fins a l'any 1849, quan Hippolyte Fizeau realitzà una mesura directa de la velocitat de la llum. Fizeau va fer un experiment que consistia a enviar un raig de llum (provinent d'un focus), sobre un mirall que es trobava a gran distància, interposant entre el focus emetent i el mirall una roda dentada. Aquesta disposició obligava que el raig de llum hagués de passar per l'espai consecutiu entre dues dents del marge de la roda (una roda giratòria), rebotar en el mirall, i tornar a passar pel mateix espai.
La distància que separava la roda i el mirall fou de 8 633 metres. Des del moment en què la llum travessa l'espai consecutiu de les dents, es reflecteix en el mirall, i torna a passar pel mateix espai de les dents, es dona el doble de distància (8 633 m · 2 = 17 326 m). Una vegada calculada la distància que recorria la llum, calia saber el temps en què aquesta ho feia. Tenint en compte que la roda dentada girava a 12,6 revolucions per segon, i que la roda presentava 720 dents (1 440 sumant els espais), es calculà el temps necessari perquè una dent pogués ocupar el lloc d'un espai en contacte:
Una vegada es disposà de la distància i el temps en què la llum ho realitzà, Fizeau va calcular la velocitat de la llum (posat que la velocitat és el resultat de dividir la distància entre el temps):
El resultat d'aquest experiment fou el que més s'acostà a la velocitat de la llum. Posteriorment, als anys 50, un científic anglès i un americà van determinar mitjançant una freqüència de ressonància d'ones de ràdio, que la velocitat de la llum era exactament de 299.790 km/s. Això no obstant, ho arrodonim als 300.000 km/s.
En diversos sistemes
[modifica]Espai lliure
[modifica]En unitats del SI, la velocitat de qualsevol radiació electromagnètica en espai lliure està relacionada amb la constant elèctrica ε0 (també anomenada permitivitat de l'espai lliure) i la constant magnètica μ0 (també anomenada permeabilitat de l'espai lliure) per l'equació c02=1/(ε0 μ0).[17]
Segons l'electromagnetisme clàssic, la velocitat de la radiació electromagnètica en espai lliure és igual per a totes les freqüències. Això significa que la llum en espai lliure presenta una dispersió zero. La velocitat de la llum en espai lliure és independent de la polarització, isotròpica i independent de la força dels camps.
L'espai lliure és un "estat de referència". Com el zero absolut, és un estat idealitzat que en el món físic només es pot aproximar. Els mesuraments en qualsevol medi real, com ara l'aire[18][19] o un medi pertorbat per la gravetat,[20] han de tenir en compte l'índex refractiu del medi per relacionar-los amb l'estàndard de referència de l'espai lliure.
Buit realitzable
[modifica]Tot i que l'espai lliure és un estat de referència idealitzat no realitzable en la pràctica, alguns medis s'hi aproximen molt, com ara l'espai exterior o els ultrabuits a la Terra.
Un model senzill que sovint es fa servir per a representar un buit semblant a l'espai lliure és aquell en què la permitivitat i la permeabilitat magnètiques són constants amb els valors ε0 i μ0. En aquest model clàssic, la velocitat de la llum és igual per a totes les longituds d'ona, i existeix una isotropia perfecta, dispersió zero, una linealitat perfecta i un dicroisme perfecte. L'índex refractiu d'aquest model clàssic és la unitat.
La teoria electrodinàmica quàntica prediu desviacions d'un índex refractiu unitari al buit quàntic per als camps electromagnètics extremament forts.[21] Fins ara, no hi ha hagut cap confirmació experimental d'aquest efecte.
Els mesurament basats en l'arribada de radiacions electromagnètiques d'esdeveniments astrofísics llunyans han posat límits restrictius a la variació possible de la velocitat de la llum amb la freqüència a l'espai exterior.[22]
Medis transparents
[modifica]Quan un pols lumínic compost de múltiples freqüències passa per materials transparents, la velocitat de la llum es caracteritza per dues velocitats: la velocitat de fase i la velocitat de grup. La velocitat de fase de la llum es pot esbrinar a partir del coneixement de l'índex de refracció dependent de la freqüència:
en què εr és la permitivitat relativa del material, i μr és la seva permeabilitat relativa.
La velocitat de grup de l'ona és la velocitat a la qual l'embolcall de pols viatja a través del medi, i depèn del contingut en freqüències de pols i de les propietats del medi. Quan una ona té diferents velocitats de fase i de grup, es diu que pateix dispersió. Si la llum que passa pel medi és monocromàtica, la velocitat de fase sol ser considerada la "velocitat de la llum".
Quan la llum penetra en materials, la seva energia és absorbida. En el cas dels materials transparents (dielèctrics), aquesta energia és ràpidament irradiada de nou. Tanmateix, aquesta absorció i reirradiació causa un retard. A mesura que la llum viatja a través d'un material dielèctric, pateix una absorció i una reirradiació contínues. Per tant, quan es diu que la velocitat de la llum en un medi és inferior a c, cal interpretar que això es refereix a la velocitat de la propagació d'energia al nivell macroscòpic. Al nivell atòmic, les ones electromagnètiques viatgen sempre a c en l'espai buit entre els àtoms. Dos factors influeixen en aquest alentiment: una absorció més forta que provoca un camí més curt entre cada cicle de reirradiació i retards més llargs. Per consegüent, l'alentiment és el producte d'aquests dos factors. Aquesta reducció de la velocitat també és la responsable del corbament de la llum a la interfície entre dos materials amb diferents índexs de refractius, un fenomen conegut com a refracció.
L'índex refractiu de l'aire és només una mica superior a 1.[23] Medis més densos, com l'aigua i el vidre, tenen índexs refractius d'entre 1,3 i 1,5 per a la llum visible. Els diamants tenen un índex refractiu d'aproximadament 2,4.
La velocitat de la llum com a velocitat màxima de transferència d'informació
[modifica]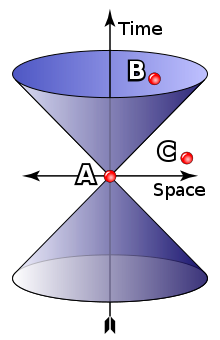
Causalitat i transferència d'informació
[modifica]Segons la teoria de la relativitat espacial, la causalitat seria violada si la informació pogués viatjar més ràpid que c en algun marc de referència, car aquest marc esdevindria un marc privilegiat per sobre de tots els altres.[24][25][26] En alguns altres marcs de referència, la informació seria rebuda abans de ser enviada, de manera que l'«efecte» seria observat abans que la «causa». Mai no s'ha observat tal violació de la causalitat.[27]
La informació es propaga des d'i fins a un punt formant regions definides per un con de llum. L'interval AB del diagrama a la dreta és "semblant al temps" (és a dir, hi ha un marc de referència en què l'esdeveniment A i l'esdeveniment B es produeixen al mateix punt de l'espai, separats únicament per la seva ocurrència en temps diferents, i si A precedeix B en aquest marc, aleshores el precedeix en tots els marcs; no hi ha cap marc de referència en què A i B es produeixin alhora). Per tant, hipotèticament, és possible que la matèria (o la informació) viatgi d'A a B, de manera que hi pugui haver una relació causal (i és A la "causa" i B l'"efecte").
D'altra banda, l'interval AC del diagrama a la dreta és «semblant a l'espai» (és a dir, hi ha un marc de referència en què l'esdeveniment A i l'esdeveniment C es produeixen alhora, separats únicament per l'espai; vegeu simultaneïtat). Tanmateix, també hi ha marcs en què A precedeix C (com es mostra) o en què C precedeix A. Deixant de banda alguna manera de moure's més ràpid que la llum, és impossible que la matèria (o la informació) viatgi de A a C o de C a A. Per tant, no hi ha connexió causal entre A i C.
Referències
[modifica]- ↑ Penrose 2004, p. 410-411:
« (anglès) the most accurate standard for the metre is conveniently defined so that there are exactly 299,792,458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris. (català) l'estàndard del metre més precís es defineix convenientment de manera que n'hi hagi exactament 299.792.458 en la distància que recorre la llum en un segon estàndard, resultant en un valor del metre que coincideix de manera molt precisa l'actualment inadequat precís estàndard del metre de París. » — Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe - ↑ Uzan i Leclercq, 2008, p. 43-44.
- ↑ «How is the speed of light measured?» (en anglès).
- ↑ Stachel, JJ. Einstein from "B" to "Z" – Volume 9 of Einstein studies. Springer, 2002, p. 226. ISBN 0-8176-4143-2.
- ↑ 5,0 5,1 International Bureau of Weights and Measures. The International System of Units (SI). 8a ed.. International Bureau of Weights and Measures, 2006, p. 112. ISBN 92-822-2213-6.
- ↑ La C majúscula és el símbol del Sistema Internacional d'Unitats (SI) del coulomb.
- ↑ Gibbs, P. «Why is c the symbol for the speed of light?». Usenet Physics FAQ. University of California, Riverside, 2004. Arxivat de l'original el 2009-11-17. [Consulta: 16 novembre 2009].
- ↑ Mendelson, KS «The story of c». American Journal of Physics, 74, 11, 2006, pàg. 995–997. Bibcode: 2006AmJPh..74..995M. DOI: 10.1119/1.2238887.
- ↑ See for example:
- Lide, DR. CRC Handbook of Chemistry and Physics. CRC Press, 2004, p. 2–9. ISBN 0-8493-0485-7.
- Harris, JW [et al.].. Handbook of Physics. Springer, 2002, p. 499. ISBN 0-387-95269-1.
- Whitaker, JC. The Electronics Handbook. CRC Press, 2005, p. 235. ISBN 0-8493-1889-0.
- Cohen, ER [et al.].. Quantities, Units and Symbols in Physical Chemistry. 3a edició. Royal Society of Chemistry, 2007, p. 184. ISBN 0-85404-433-7.
- ↑ Sydenham, PH. «Measurement of length». A: Boyes, W. Instrumentation Reference Book. 3a edició. Butterworth–Heinemann, 2003, p. 56. ISBN 0-7506-7123-8. «... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ...»
- ↑ «CODATA value: Speed of Light in Vacuum». The NIST reference on Constants, Units, and Uncertainty. NIST. [Consulta: 21 agost 2009].
- ↑ Jespersen, J; Fitz-Randolph, J; Robb, J. From Sundials to Atomic Clocks: Understanding Time and Frequency. 1977a ed.. Courier Dover, 1999, p. 280. ISBN 0-486-40913-9.
- ↑ Lawrie, ID. «Appendix C: Natural units». A: A Unified Grand Tour of Theoretical Physics. 2a edició. CRC Press, 2002, p. 540. ISBN 0-7503-0604-1.
- ↑ Hsu, L. «Appendix A: Systems of units and the development of relativity theories». A: A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance. 2a edició. World Scientific, 2006, p. 427–8. ISBN 981-256-651-1.
- ↑ Hall, S.H. i Hall, G.W. i McCall, J.A.. High Speed Digital System Design: A Handbook of Interconnect Theory and Design Practices. Wiley New York, 2000.
- ↑ E. Gad, M. Nakla & R. Achar. «Model-order reduction of high-speed interconnects using integrated congruence transform». A: Joost Rommes, Wil Schilders, Henk Van Der Vorst. Model Order Reduction. Springer, 2008, p. 362. ISBN 3540788409.
- ↑ W. Panofsky, M. Phillips. Classical Electricity and Magnetism. Addison Wesley, 1962, p. 182.
- ↑ B. G. Zagar. «Laser Interferometer Displacement Sensors; §6.5». A: J. G. Webster. The Measurement, Instrumentation, and Sensors Handbook. CRC Press, 1999, p. 6-69. ISBN 0849383471.
- ↑ J. Flügge et al.. «Fundamental length metrology: Practical issues; §D.2.1.3». A: C. E. Webb & J. D. C. Jones. Handbook of Laser Technology and Applications. Taylor & Francis, 2004, p. 1737 ff. ISBN 0750309660.
- ↑ La relativitat general prediu una distorsió de l'espai per part de la gravetat que es pot expressar com un índex efectiu de refracció. La velocitat de la llum en un buit ideal només assoleix el seu màxim en gravetat zero. Vegeu K. K. Nandi et al. «An analog of the Fizeau effect in an effective optical medium». Phys Rev D, 67, 2003., Henry Lipson & D. S. Tannhauser. Optical Physics. Cambridge University Press, 1995, p. 33. ISBN 0521436311. i HE Puthoff. «Polarizable vacuum approach to general relativity». A: R. L. Amaroso et al.. Gravitation and Cosmology. Springer, 2002, p. 431. ISBN 1402008856.. Podeu trobar un resum dels treballs més recents a Y. E. Xing Hao & L. I. N. Qiang «Inhomogeneous vacuum: An alternative interpretation of curved spacetime». Chin Phys Lett, 25, 2008, pàg. 1571. DOI: 10.1088/0256-307X/25/5/014.
- ↑ Walter Dittrich & Gies H.. Probing the quantum vacuum: perturbative effective action approach. Berlín: Springer, 2000, p. 13, per exemple. ISBN 3540674284.
- ↑ J. D. Jackson. Classical Electrodynamics, Second edition. John Wiley & Sons, 1975, p. 514-515. ISBN 0-471-43132-x.
- ↑ Michael De Podesta. Understanding the Properites of Matter. CRC Press, 2002, p. 131. ISBN 0415257883.
- ↑ Vlatko Vedral. Introduction to quantum information science. Oxford University Press, 2006, p. 49. ISBN 0199215707.
- ↑ Brian Greene. The Elegant Universe. WW Norton & Co., 2003, p. 56. ISBN 0393058581.
- ↑ PCW Davies. The Forces of Nature. Cambridge University Press, 1979, p. 128. ISBN 052122523X.
- ↑ Y. Z. Zhang, Y.-C. Chang. Special Relativity and Its Experimental Foundations. World Scientific, 1998, p. 31, 171. ISBN 9810227493.
Bibliografia
[modifica]- Penrose, Roger. The Road to Reality: A Complete Guide to the Laws of the Universe (en anglès). Vintage Books, 2004. ISBN 978-0-679-77631-4.
- Uzan, Jean-Philippe; Leclercq, Bénédicte. The Natural Laws of the Universe: Understanding Fundamental Constants (en anglès). Springer, 2008. ISBN 0-387-73454-6.
Bibliografia històrica
[modifica]- Rømer, Ole «Démonstration touchant le mouvement de la lumière». Journal des sçavans, 1676, pàg. 223–236. Arxivat de l'original el 2006-06-21 [Consulta: 6 octubre 2007]. Arxivat 2006-06-21 a Wayback Machine. (francès). Traduït com a «A Demonstration concerning the Motion of Light». Philosophical Transactions of the Royal Society, 136, 1677, pàg. 893–894. Arxivat de l'original el 2007-07-29 [Consulta: 27 juny 2009]. Arxivat 2007-07-29 a Wayback Machine.
- Halley, Edmund «Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London». Philosophical Transactions of the Royal Society, 18, 214, 1694, pàg. 237–256.
- Fizeau, H. L. (1849). "Sur une expérience relative à la vitesse de propagation de la lumière". 29: 90–92, 132
- Foucault, J. L. (1862). "Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil". 55: 501–503, 792–796
- Michelson, A. A. (1878). "[1]". Experimental Determination of the Velocity of Light 27: 71–77
- Newcomb, Simon «The Velocity of Light». Nature, 1886, p. 29–32.
- Perrotin, Joseph «Sur la vitesse de la lumière». C. R. Acad. Sci. Paris, 131, 1900, p. 731–734.
- Michelson, A. A.; Pease, F. G.; Pearson, F. «Measurement Of The Velocity Of Light In A Partial Vacuum». Astrophys. J., 82, 1935, p. 26–61. DOI: 10.1086/143655.
Bibliografia moderna
[modifica]- Brillouin, Léon. Wave propagation and group velocity. Academic Press, 1960.
- Jackson, John David. Classical electrodynamics. 2a edició. John Wiley & Sons, 1975. ISBN 0-471-30932-X.
- MacKay, R. J.; Oldford, R. W. «Scientific Method, Statistical Method and the Speed of Light». Statistical Science, 15, 3, 2000, p. 254–278. DOI: 10.1214/ss/1009212817.
- Keiser, Gerd. Optical Fiber Communications. 3a edició. McGraw-Hill, 2000, p. 32. ISBN 0072321016.
- Y. Jack Ng. «Quantum Foam and Quantum Gravity Phenomenology». A: Giovanni Amelino-Camelia & Jerzy Kowalski-Glikman (editors). Planck Scale Effects in Astrophysics and Cosmology. Springer, 2004, p. 321ff. ISBN 3540252630.
Enllaços externs
[modifica]- Velocitat de la llum en el buit al web del NIST (en anglès).
- Com es mesura la velocitat de la llum? (anglès)
- Definició del metre al web de l'Oficina Internacional de Pesos i Mesures (anglès)
- AstroMía.com (informació sobre la velocitat de la llum). (en castellà)




