Buit QCD
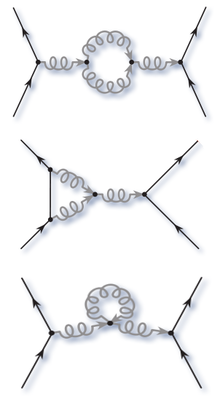
El buit QCD és l'estat de buit quàntic de la cromodinàmica quàntica (QCD). És un exemple d'estat de buit no perturbador, caracteritzat per condensats que no s'esvaeixen com el condensat de gluó i el condensat de quark en la teoria completa que inclou els quarks. La presència d'aquests condensats caracteritza la fase confinada de la matèria dels quarks.[1]
Simetries i trencament de simetria
[modifica]Simetries del QCD Lagrangià
[modifica]Com qualsevol teoria quàntica relativista de camps, QCD gaudeix de la simetria de Poincaré incloent les simetries discretes CPT (cadascuna de les quals es realitza). A part d'aquestes simetries espai-temps, també té simetries internes. Com que QCD és una teoria de gauge SU(3), té una simetria de gauge SU(3) local.[2]
Com que té molts sabors de quarks, té un sabor aproximat i una simetria quiral. Es diu que aquesta aproximació implica el límit quiral de QCD. D'aquestes simetries quirals, la simetria del nombre barió és exacta. Algunes de les simetries trencades inclouen la simetria axial U(1) del grup de sabors. Això es trenca per l'anomalia quiral. La presència d'instantons implicada per aquesta anomalia també trenca la simetria CP.[3]
En resum, el QCD Lagrangià té les simetries següents:
- Simetria de Poincaré i invariància CPT
- SU(3) simetria de calibre local
- SU(Nf) global aproximat SU(Nf) × SU(Nf) de simetria quiral i la simetria del nombre barió U(1).
Les simetries clàssiques següents es trenquen al lagrangià QCD:
- escala, és a dir, simetria conforme (a través de l'anomalia d'escala), donant lloc a la llibertat asimptòtica
- la part axial de la simetria quiral del sabor U(1) (a través de l'anomalia quiral), donant lloc al fort problema de CP.
Trencament de simetria espontània
[modifica]Quan l'Hamiltonià d'un sistema (o el Lagrangià) té una certa simetria, però el buit no, es diu que s'ha produït una ruptura espontània de simetria (SSB).[4]
Un exemple familiar de SSB és en materials ferromagnètics. Microscòpicament, el material es compon d'àtoms amb un gir que no s'esvaeix, cadascun dels quals actua com un petit imant de barra, és a dir, un dipol magnètic. L'hammiltonià del material, que descriu la interacció dels dipols veïns, és invariant sota rotacions. A alta temperatura, no hi ha magnetització d'una gran mostra del material. Llavors es diu que la simetria de l'hammiltonià és realitzada pel sistema. Tanmateix, a baixa temperatura, podria haver-hi una magnetització global. Aquesta magnetització té una direcció preferida, ja que es pot distingir el pol magnètic nord de la mostra del pol magnètic sud. En aquest cas, hi ha ruptura de simetria espontània de la simetria rotacional de l'Hamiltonià.
Quan es trenca espontàniament una simetria contínua, apareixen bosons sense massa, corresponents a la simetria restant. Això s'anomena fenomen Goldstone i els bosons s'anomenen bosons Goldstone.
Simetries del buit QCD
[modifica]La simetria de sabor quiral SU( Nf ) ×SU( Nf ) del lagrangià QCD es trenca en l'estat de buit de la teoria. La simetria de l'estat del buit és la part diagonal SU( Nf ) del grup quiral. El diagnòstic d'això és la formació d'un condensat quiral que no s'esvaeix ⟨ψiψi⟩, on ψi és l'operador de camp de quark i es suma l'índex de sabor i. Els bosons de Goldstone del trencament de simetria són els mesons pseudoescalars.
Quan Nf = 2, és a dir, només els quarks amunt i avall es tracten com a sense massa, els tres pions són els bosons de Goldstone. Quan el quark estrany també es tracta com sense massa, és a dir, Nf = 3, els vuit mesons pseudoescalars del model de quark es converteixen en bosons de Goldstone. Les masses reals d'aquests mesons s'obtenen en la teoria de la pertorbació quiral mitjançant una expansió de les (petites) masses reals dels quarks.
En altres fases de la matèria de quark, es pot recuperar la simetria completa del sabor quiral o trencar-se de maneres completament diferents.
Referències
[modifica]- ↑ «Demystifying the QCD Vacuum - Part 1 - The Standard Story» (en anglès americà), 26-05-2017. [Consulta: 15 març 2024].
- ↑ «QCD Vacuum [The Physics Travel Guide]» (en anglès). [Consulta: 15 març 2024].
- ↑ Chernodub, Maxim. QCD Vacuum as Dual Superconductor: Quark Confinement and Topology (en anglès). Singapore: Springer Nature, 2020, p. 1–42. DOI 10.1007/978-981-15-8818-1_23-1. ISBN 978-981-15-8818-1.
- ↑ «The QCD Vacuum, Hadrons and Superdense Matter | World Scientific Lecture Notes in Physics» (en anglès). DOI: 10.1142/5367. [Consulta: 15 març 2024].
