Codi tòric

El codi tòric és un codi de correcció d'errors quàntics topològics i un exemple de codi estabilitzador, definit en una xarxa de spin bidimensional. És el més senzill i més ben estudiat dels models dobles quàntics. També és l'exemple més simple d'ordre topològic: ordre topològic Z₂ (estudiat per primera vegada en el context del líquid d'espiín Z₂ el 1991). El codi tòric també es pot considerar com una teoria de calibre de gelosia Z₂ en un límit particular. Va ser presentat per Alexei Kitaev.

El codi tòric rep el seu nom de les seves condicions de límit periòdiques, donant-li la forma d'un tor. Aquestes condicions donen al model invariància translacional, que és útil per a l'estudi analític. No obstant això, algunes realitzacions experimentals requereixen condicions de límit obertes, que permeten incrustar el sistema en una superfície 2D. El codi resultant es coneix normalment com a codi pla. Això té un comportament idèntic al codi tòric en la majoria dels casos, però no en tots.

Càlcul i correcció d'errors

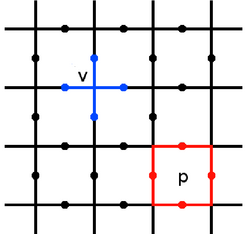
El codi tòric es defineix en una gelosia bidimensional, normalment escollida per ser la xarxa quadrada, amb un grau de llibertat de espín ½ situat a cada aresta. Es trien per ser periòdics. Els operadors estabilitzadors es defineixen als girs al voltant de cada vèrtex $v$ i plaqueta  (o cara, és a dir, un vèrtex de la gelosia dual) $p$ de la gelosia de la següent manera,

$A_{v}=\prod _{i\in v}\sigma _{i}^{x},\,\,B_{p}=\prod _{i\in p}\sigma _{i}^{z}.$

On aquí fem servir $i\in v$ per indicar les arestes que toquen el vèrtex $v$, i $i\in p$ per indicar les vores que envolten la plaqueta $p$. L'espai estabilitzador del codi és aquell pel qual tots els estabilitzadors actuen de manera trivial, per tant, per a qualsevol estat $|\psi \rangle$ en aquest espai ho sosté

$A_{v}|\psi \rangle =|\psi \rangle ,\,\,\forall v,\,\,B_{p}|\psi \rangle =|\psi \rangle ,\,\,\forall p.$

Per al codi tòric, aquest espai és de quatre dimensions i, per tant, es pot utilitzar per emmagatzemar dos qubits d'informació quàntica. Això es pot provar tenint en compte el nombre d'operadors estabilitzadors independents. L'aparició d'errors mourà l'estat fora de l'espai estabilitzador, donant lloc a vèrtexs i plaquetes per als quals la condició anterior no es compleix. Les posicions d'aquestes violacions és la síndrome del codi, que es pot utilitzar per a la correcció d'errors.

Una secció del codi tòric. Es destaquen un vèrtex i una plaqueta, juntament amb els girs utilitzats en la definició dels seus estabilitzadors.

La naturalesa única dels codis topològics, com ara el codi tòric, és que les violacions de l'estabilitzador es poden interpretar com a quasipartícules. Concretament, si el codi està en un estat $|\phi \rangle$ tal que,

$A_{v}|\phi \rangle =-|\phi \rangle$

una quasipartícula coneguda com a $e$ es pot dir que qualsevol persona existeix al vèrtex $v$. De la mateixa manera les violacions de la $B_{p}$ estan associats amb els anomenats $m$ anyons a les plaquetes. L'espai estabilitzador correspon, per tant, al buit anyònic. Els errors d'un sol gir fan que es creïn i es transportin parelles d'anyons al voltant de la gelosia.

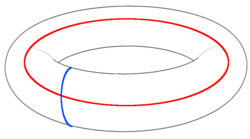
Quan els errors creen un parell anyon i mouen els anyons, es pot imaginar un camí que connecta els dos compost per tots els enllaços sobre els quals s'ha actuat. Si els anyons es troben i són aniquilats, aquest camí descriu un bucle. Si el bucle és topològicament trivial, no té cap efecte sobre la informació emmagatzemada. L'aniquilació dels anyons, en aquest cas, corregeix tots els errors implicats en la seva creació i transport. Tanmateix, si el bucle és topològicament no trivial, encara que la reaniquilació dels anyons retorna l'estat a l'espai estabilitzador, també implementa una operació lògica sobre la informació emmagatzemada. Els errors, en aquest cas, no es corregeixen, sinó que es consoliden.

Els bucles topològicament no trivials del torus. Moure qualsevol persona al llarg d'aquests implementa operadors lògics de Pauli als qubits emmagatzemats.

Considereu el model de soroll per al qual es produeixen errors de bits i de fase independentment a cada gir, tots dos amb probabilitat p. Quan p és baix, això crearà parells poc distribuïts d'anyons que no s'han mogut lluny del seu punt de creació. La correcció es pot aconseguir identificant els parells en què es van crear els anyons (fins a una classe d'equivalència) i després tornar-los a aniquilar per eliminar els errors. Tanmateix, a mesura que p augmenta, es fa més ambigu quant a com es poden aparellar els anyons sense arriscar la formació de bucles topològicament no trivials. Això dóna un llindar de probabilitat, sota el qual la correcció d'errors serà gairebé segura. Mitjançant un mapeig al model Ising d'enllaç aleatori, s'ha trobat que aquesta probabilitat crítica és al voltant de l'11%.

També es poden considerar altres models d'error i trobar llindars. En tots els casos estudiats fins ara, s'ha trobat que el codi satura el límit Hashing. Per a alguns models d'error, com els errors esbiaixats on els errors de bits es produeixen amb més freqüència que els errors de fase o viceversa, s'han d'utilitzar reticules diferents de la xarxa quadrada per aconseguir els llindars òptims.

Aquests llindars són límits superiors i són inútils tret que es trobin algorismes eficients per aconseguir-los. L'algoritme més utilitzat és la concordança perfecta del pes mínim. Quan s'aplica al model de soroll amb errors de bit i flip independents, s'aconsegueix un llindar al voltant del 10,5%. Això només queda una mica per sota del màxim de l'11%. Tanmateix, la concordança no funciona tan bé quan hi ha correlacions entre els errors de bit i de fase, com ara amb el soroll despolaritzant.

S'han considerat els mitjans per realitzar el càlcul quàntic sobre la informació lògica emmagatzemada dins del codi tòric, amb les propietats del codi que proporcionen tolerància a errors. S'ha demostrat que l'ampliació de l'espai de l'estabilitzador mitjançant "forats", vèrtexs o plaquetes sobre els quals no s'apliquen estabilitzadors, permet codificar molts qubits al codi. Tanmateix, un conjunt universal de portes unitàries no es pot implementar de manera tolerant a errors mitjançant operacions unitàries i, per tant, calen tècniques addicionals per aconseguir la computació quàntica. Per exemple, la computació quàntica universal es pot aconseguir preparant estats màgics mitjançant talls quàntics codificats anomenats tidBits que s'utilitzen per teletransportar-se a les portes addicionals necessàries quan es substitueixen com a qubit. A més, la preparació d'estats màgics ha de ser tolerant a errors, cosa que es pot aconseguir mitjançant la destil·lació d'estats màgics en estats màgics sorollosos. S'ha trobat un esquema basat en mesures per a la computació quàntica basat en aquest principi, el llindar d'error del qual és el més alt conegut per a una arquitectura bidimensional.