Ordinador quàntic unidireccional

Les tècniques basades en la mesura consisteixen a enredar un cúmul de qubits i realitzar un conjunt de mesures. Gràcies a la correlació entre els qubits entrellaçats, el flux d'informació (d'esquerra a dreta) es realitza mitjançant les mesures dels qubits físics del clúster.

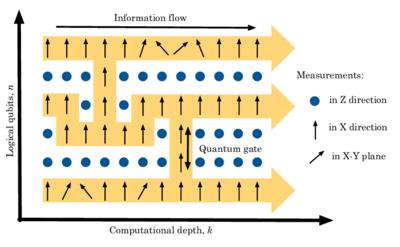
L'ordinador quàntic unidireccional, també conegut com ordinador quàntic basat en mesures (MBQC), és un mètode de computació quàntica que primer prepara un estat de recurs entrellaçat, normalment un estat de clúster o estat de gràfic, i després realitza mesures d'un qubit únic. És "unidireccional" perquè les mesures destrueixen l'estat del recurs.

El resultat de cada mesura individual és aleatori, però estan relacionats de tal manera que el càlcul sempre té èxit. En general, les opcions de base per a mesures posteriors han de dependre dels resultats de mesures anteriors i, per tant, no es poden realitzar totes les mesures alhora.

La implementació de MBQC es considera principalment per a dispositius fotònics, a causa de la dificultat d'entrellaçar fotons sense mesurar-los i la senzillesa de crear-los i mesurar-los. Tanmateix, MBQC també és possible amb qubits basats en matèria. El procés d'entrellaçament i mesura es pot descriure amb l'ajuda d'eines de gràfics i teoria de grups, en particular pels elements del grup estabilitzador.

Definició

El propòsit de la computació quàntica se centra a construir una teoria de la informació amb les característiques de la mecànica quàntica: en lloc de codificar una unitat binària d'informació (bit), que es pot canviar a 1 o 0, una unitat binària quàntica d'informació (qubit) pot simultàniament. torn a ser 0 i 1 alhora, gràcies al fenomen anomenat superposició. Una altra característica clau per a la computació quàntica es basa en l'entrellat entre els qubits.

Un circuit quàntic que implementa l'algorisme de Bernstein-Vazirani: $H$ i $U_{f}$ representen les portes lògiques (operadors unitaris) que actuen sobre el registre de qubits. En el marc MBQC, les portes lògiques es realitzen entrellaçant els qubits i mesurant els auxiliars.

En el model de porta lògica quàntica, es prepara un conjunt de qubits, anomenat registre, al començament del càlcul, després s'implementa un conjunt d'operacions lògiques sobre els qubits, portades per operadors unitaris. Un circuit quàntic està format per un registre de qubits sobre els quals s'apliquen transformacions unitàries sobre els qubits. En el càlcul quàntic basat en mesures, en comptes d'implementar una operació lògica mitjançant transformacions unitàries, la mateixa operació s'executa entrellaçant un nombre. $k$ de qubits d'entrada amb un clúster de $a$ qubits auxiliars, que formen un estat d'origen global de $a+k=n$ qubits i després mesurant un nombre $m$ d'ells. La resta $k=n-a$ els qubits de sortida es veuran afectats per les mesures a causa de l'entrellat amb els qubits mesurats. S'ha demostrat que l'ordinador unidireccional és un ordinador quàntic universal, el que significa que pot reproduir qualsevol operació unitària en un nombre arbitrari de qubits.

Procediment general

El procés estàndard de la computació quàntica basada en la mesura consta de tres passos: entrellaçar els qubits, mesurar els ancillae (qubits auxiliars) i corregir les sortides. En el primer pas, els qubits s'entrellacen per tal de preparar l'estat d'origen. En el segon pas, es mesuren les ancillaes, afectant l'estat dels qubits de sortida. No obstant això, les sortides de mesura són un resultat no determinista, a causa de la naturalesa indeterminada de la mecànica quàntica: per dur a terme el càlcul d'una manera determinista, s'introdueixen alguns operadors de correcció, anomenats subproductes.

Preparació de l'estat d'origen

El funcionament de la CZ als esquemes de circuits.

Al començament del càlcul, els qubits es poden distingir en dues categories: els qubits d'entrada i els auxiliars. Les entrades representen els qubits establerts en un genèric $|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$ estat, sobre el qual s'han d'actuar algunes transformacions unitàries. Per tal de preparar l'estat d'origen, tots els qubits auxiliars s'han de preparar al fitxer $|+\rangle$ estat:

$|+\rangle ={\tfrac {|0\rangle +|1\rangle }{\sqrt {2}}},$

on $|0\rangle$ i $|1\rangle$ són la codificació quàntica de la clàssica $0$ i $1$ bits:

$|0\rangle ={\begin{pmatrix}1\\0\end{pmatrix}};\quad |1\rangle ={\begin{pmatrix}0\\1\end{pmatrix}}$

Un registre amb $n$ Els qubits s'establiran com a $|+\rangle ^{\otimes n}$. A continuació, l'entrellat entre dos qubits es pot realitzar aplicant un (Controlat) $CZ$ funcionament de la porta. La representació matricial d'aquest operador de dos qubits ve donada per

$CZ={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\end{bmatrix}}.$

L'acció d'a $CZ$ La porta de més de dos qubits es pot descriure amb el sistema següent:

${\begin{cases}CZ|0+\rangle =|0+\rangle \\CZ|0-\rangle =|0-\rangle \\CZ|1+\rangle =|1-\rangle \\CZ|1-\rangle =|1+\rangle \end{cases}}$

En aplicar a $CZ$ porta sobre dues ancillae a la $|+\rangle$ estat, l'estat global

$CZ|++\rangle ={\frac {|0+\rangle +|1-\rangle }{\sqrt {2}}}$

es converteix en un parell de qubits entrellaçats. Quan s'entrellacen dues ancillae, no es dóna cap importància a quin és el qubit de control i quin és l'objectiu, en la mesura que el resultat resulta ser el mateix. De la mateixa manera, com el $CZ$ les portes es representen en forma diagonal, totes es desplacen entre si i no es dóna cap importància sobre quins qubits s'entrellaçaran primer.

Els fotons són el sistema qubit més comú que s'utilitza en el context de la computació quàntica unidireccional. Tanmateix, determinista $CZ$ Les portes entre fotons són difícils de realitzar. Per tant, normalment es consideren portes d'enredament probabilistes, com ara les mesures d'estat de Bell. A més, els emissors quàntics com els àtoms o els punts quàntics es poden utilitzar per crear entrellaçament determinista entre qubits fotònics.

Mesura dels qubits

Implementació de portes X i Z sobre dos qubits en els diagrames de circuits.

El procés de mesura sobre un estat d'una sola partícula es pot descriure projectant l'estat en el vector propi d'un observable. Considereu un observable $O$ amb dos possibles vectors propis, per exemple $|o_{1}\rangle$ i $|o_{2}\rangle$, i suposem que hem de tractar amb un sistema quàntic multipartícules $|\Psi \rangle$. Mesurant el $i$ -è qubit pel $O$ mitjans observables per projectar el $|\Psi \rangle$ estat sobre els vectors propis de $O$ :

$|\Psi '\rangle =|o_{i}\rangle \langle o_{i}|\Psi \rangle$

L'estat real de la $i$ -El qubit és ara $|o_{i}\rangle$, que pot arribar a ser $|o_{1}\rangle$ o $|o_{2}\rangle$, segons el resultat de la mesura (que és probabilista en mecànica quàntica). La projecció de mesura es pot realitzar sobre els estats propis de la $M(\theta )=\cos(\theta )X+\sin(\theta )Y$ observable:

$M(\theta )=\cos(\theta ){\begin{bmatrix}0&1\\1&0\end{bmatrix}}+\sin(\theta ){\begin{bmatrix}0&-i\\i&0\end{bmatrix}}={\begin{bmatrix}0&e^{-i\theta }\\e^{i\theta }&0\end{bmatrix}}$

on $X$ i $Y$ pertanyen a les matrius Pauli. Els vectors propis de $M(\theta )$ són $|\theta _{\pm }\rangle =|0\rangle \pm e^{i\theta }|1\rangle$. Mesurar un qubit al $X$ - $Y$ avió, és a dir, pel $M(\theta )$ observable, vol dir projectar-lo $|\theta _{+}\rangle$ o $|\theta _{-}\rangle$. En la computació quàntica unidireccional, un cop s'ha mesurat un qubit, no hi ha manera de reciclar-lo en el flux de càlcul. Per tant, en comptes d'utilitzar $|o_{i}\rangle \langle o_{i}|$ notació, és comú trobar $\langle o_{i}|$ per indicar una mesura projectiva sobre el $i$-è qubit.

Maquinari i aplicacions

Ordinador quàntic d'estat de clúster topològic

El càlcul basat en la mesura en un estat de clúster de gelosia 3D periòdic es pot utilitzar per implementar la correcció d'errors quàntics topològics. El càlcul de l'estat del clúster topològic està estretament relacionat amb el codi tòric de Kitaev, ja que l'estat del clúster topològic 3D es pot construir i mesurar al llarg del temps mitjançant una seqüència repetida de portes en una matriu 2D.

Implementacions

El càlcul quàntic unidireccional s'ha demostrat executant l'algorisme de Grover de 2 qubits en un estat de clúster de fotons de 2x2. S'ha proposat un ordinador quàntic d'òptica lineal basat en el càlcul unidireccional.

Els estats de clúster també s'han creat en reticules òptiques, però no es van utilitzar per al càlcul ja que els qubits de l'àtom estaven massa a prop per mesurar-los individualment.

L'estat AKLT com a recurs

S'ha demostrat que el (espin ${\tfrac {3}{2}}$) L'estat AKLT en una gelosia de bresca 2D es pot utilitzar com a recurs per a MBQC. Més recentment s'ha demostrat que un estat AKLT de barreja de spin es pot utilitzar com a recurs.