Coeficient de determinació

El coeficient de determinació, també el coeficient de determinació (del llatí determinatio “delimitació, determinació” o determinare “límit”, “determinar”, “determinar” i coefficient “participar”), es denota per , és una figura clau en les estadístiques per avaluar la bondat d'ajust d'una regressió. El coeficient de determinació es basa en la descomposició de la suma de quadrats, en la qual la suma total de quadrats es descompon en la suma de quadrats explicada pel model de regressió d'una banda i la suma residual de quadrats de l'altra. Tanmateix, hi ha diverses definicions diferents i no equivalents del coeficient de determinació.[1]
El coeficient de determinació està estretament relacionat amb altres mesures de qualitat del model per provar la funció de regressió, com ara: Per exemple, l'error estàndard de regressió i l'estadística F. Com que el coeficient de determinació augmenta en incloure variables addicionals i hi ha un risc de sobreajustament, el coeficient de determinació ajustat s'utilitza normalment per a aplicacions pràctiques. En contrast amb el coeficient de determinació no ajustat, el coeficient de determinació ajustat "castiga" la inclusió de totes les variables explicatives afegides.[2]
Tot i que el coeficient de determinació és la mesura més utilitzada per quantificar la bondat global d'ajust d'una regressió, sovint s'interpreta i s'aplica malament, també perquè moltes definicions alternatives del coeficient de determinació no són equivalents en regressió a través de l'origen.
El coeficient de determinació és una mesura pura de connexió. Per tant, no és possible utilitzar el coeficient de determinació per demostrar una relació causal directa entre les variables. A més, el coeficient de determinació només mostra la mida de la relació entre les variables, però no si aquesta relació és estadísticament significativa.
El pseudocoeficient de determinació i la desviació generalitzen el coeficient de determinació.

Interpretació
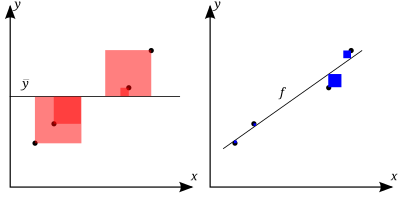
[modifica]R2 és una mesura de la bondat d'ajust d'un model.[3] En regressió, el coeficient de determinació R2 és una mesura estadística de com les prediccions de regressió s'aproximen als punts de dades reals. Una R2 d'1 indica que les prediccions de regressió s'ajusten perfectament a les dades.
Els valors de R2 fora del rang 0 a 1 es produeixen quan el model s'ajusta pitjor a les dades que el pitjor predictor de mínims quadrats possible (equivalent a un hiperpla horitzontal a una alçada igual a la mitjana de les dades observades). Això passa quan s'ha escollit un model incorrecte o s'han aplicat restriccions sense sentit per error. Si s'utilitza l'equació 1 de Kvålseth [4] (aquesta és l'equació que s'utilitza més sovint), R2 pot ser menor que zero. Si s'utilitza l'equació 2 de Kvålseth, R2 pot ser més gran que un.
En tots els casos en què s'utilitza R2, els predictors es calculen mitjançant una regressió ordinària de mínims quadrats: és a dir, minimitzant SS res. En aquest cas, R2 augmenta a mesura que augmenta el nombre de variables del model (R2 és monòton augmentant amb el nombre de variables incloses; mai disminuirà). Això il·lustra un inconvenient d'un possible ús de R2, on es podria continuar afegint variables (regressió de l'aigüera de la cuina) per augmentar el valor de R2. Per exemple, si s'està intentant predir les vendes d'un model de cotxe a partir del quilometratge de gasolina del cotxe, el preu i la potència del motor, es poden incloure factors tan irrellevants com la primera lletra del nom del model o l'alçada de l'enginyer principal que dissenya. el cotxe perquè la R2 mai disminuirà a mesura que s'afegeixin variables i probablement experimentarà un augment només a causa de l'atzar.
Això condueix a l'enfocament alternatiu de mirar la R2 ajustada. L'explicació d'aquesta estadística és gairebé la mateixa que R2 però penalitza l'estadística ja que s'inclouen variables addicionals al model. En casos diferents de l'ajustament per mínims quadrats ordinaris, l'estadística R2 es pot calcular com l'anterior i encara pot ser una mesura útil. Si l'ajust és per mínims quadrats ponderats o mínims quadrats generalitzats, es poden calcular versions alternatives de R2 adequades a aquests marcs estadístics, mentre que la R2 "crua" encara pot ser útil si s'interpreta més fàcilment. Els valors de R2 es poden calcular per a qualsevol tipus de model predictiu, que no necessita tenir una base estadística.
Referències
[modifica]- ↑ Turney, Shaun. «Coefficient of Determination (R²) | Calculation & Interpretation» (en anglès americà), 22-04-2022. [Consulta: 23 març 2024].
- ↑ «9.3 - Coefficient of Determination | STAT 500» (en anglès). [Consulta: 23 març 2024].
- ↑ Casella, Georges. Statistical inference. Second. Pacific Grove, Calif.: Duxbury/Thomson Learning, 2002, p. 556. ISBN 9788131503942.
- ↑ Kvalseth, Tarald O. The American Statistician, 39, 4, 1985, pàg. 279–285. DOI: 10.2307/2683704. JSTOR: 2683704.











