Deriva genètica

Part d'una sèrie sobre
Biologia evolutiva
Pinsans de Darwin (il·lustració de John Gould)
Temes clau Introducció a l'evolució Proves de l'evolució Descendència comuna Proves de la descendència comuna
Processos i resultats Genètica de poblacions Variació Diversitat Mutació Selecció natural Adaptació Polimorfisme Deriva genètica Flux gènic Especiació Radiació adaptativa Cooperació Coevolució Coextinció Divergència Convergència Evolució paral·lela Extinció
Història natural Origen de la vida Història de la vida Cronologia de l'evolució Evolució dels éssers humans Filogènesi Biodiversitat Biogeografia Classificació Sistemàtica evolutiva Cladística Fòssil de transició Extinció massiva
Història de la teoria de l'evolució Vista general Renaixement Abans de Darwin Darwin L'origen de les espècies Abans de la síntesi Síntesi moderna Evolució molecular Evo-devo Recerca actual Història de l'especiació Història de la paleontologia (cronologia)
Branques i aplicacions Antropologia evolutiva Aplicacions de l'evolució Computació evolutiva Criminologia biosocial Darwinisme universal Ecologia evolutiva Economia evolutiva Epistemologia evolucionista Estètica evolutiva Ètica evolucionista Evolució del llenguatge Evolució experimental Experiments sobre l'especiació Filogènia Fisiologia evolutiva Genètica ecològica Medicina evolucionista Neurociència evolucionista Paleontologia Psicologia evolucionista Selecció artificial Sistemàtica Sociobiologia Teoria evolutiva de jocs
Aspectes socials Evolució com a fet i com a teoria Aspectes socials Controvèrsia entre el creacionisme i l'evolucionisme Crítiques a l'evolució Suport científic
Categoria

La deriva genètica és el procés de variació atzarosa de les freqüències gèniques de les poblacions. És estudiat en genètica de poblacions. O sigui, en qualsevol població d'una espècie, hi ha individus amb diferents versions d'un mateix gen (al·lels). Per exemple, en una població de pèsols, unes plantes acostumen a tenir un al·lel que les fa produir llavors amb la pell llisa i unes altres una altra versió del mateix gen que fa que produeixi llavors amb la pell rugosa. Si l'efecte d'aquests gens no té valor adaptatiu (o sigui, no fa que els individus amb una versió del gen sobrevisquin o es reprodueixin millor que els que en tenen una altra), l'atzar serà l'únic mecanisme que farà variar entre les generacions successives el nombre d'individus que tenen una versió o l'altra del gen. Quan les poblacions són prou grans, els seus efectes són menyspreables, però en poblacions reduïdes la deriva pot arribar a provocar la "fixació" d'un al·lel, de manera que per atzar alguns al·lels es perden. Es diu, llavors, que la població perd diversitat genètica. És a dir, que la pèrdua progressiva de varietat d'al·lels de la població condueix a una disminució en la varietat dels caràcters genètics per homozigosi.

Quan actua la deriva genètica, tendeix a fixar un dels al·lels presents en la població. Resulta molt més probable que es fixi l'al·lel més abundant en absència d'acció d'altres forces evolutives. La velocitat de fixació d'un al·lel guarda una relació inversa amb el nombre d'individus de la població. En general, la deriva genètica és un mecanisme lent, sobretot en poblacions grans, però esdevé important quan es fragmenten les poblacions o bé es redueix la grandària de la seva població. Tot i que força relacionat, no s'ha de confondre amb l'efecte fundador, fenomen que es produeix quan un nombre petit d'individus funda una nova població, ja que si són molt pocs els individus fundadors l'atzar influeix molt en la seva composició i pot no reflectir el perfil i les freqüències genètiques presents en la població "mare".

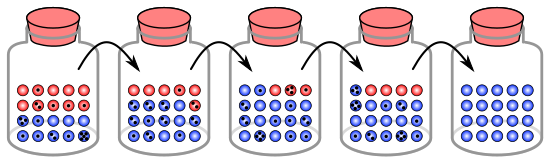
Analogia amb boles en un pot

El procés de la deriva genètica es pot il·lustrar utilitzant 20 boles en un pot per representar 20 organismes en una població. Es considera aquest pot de boles com la població inicial. La meitat de les boles del pot són vermelles i la meitat són blaves, amb cada color corresponent a un al·lel diferent d'un gen de la població. En cada nova generació, els organismes es reprodueixen a l'atzar. Per representar aquesta reproducció, es selecciona leatòriament una bola del pot original i es diposita una bola nova amb el mateix color en un pot nou. Aquesta és la "descendent" de la bola original, és a dir, que la bola original roman al seu pot. Es repeteix aquest procés fins que hi hagi 20 boles noves al segon pot. El segon pot contindrà ara 20 "descendents", o boles de diversos colors. A menys que el segon pot contingui exactament 10 boles vermelles i 10 boles blaves, s'ha produït un canvi aleatori en les freqüències d'al·lel.

Si aquest procés es repeteix diverses vegades, el nombre de boles vermells i blaus triats a cada generació fluctua. De vegades, un pot té més boles vermells que el seu pot "parent" i de vegades més blau. Aquesta fluctuació és anàloga a la deriva genètica: un canvi en la freqüència d'al·lels de la població resultant d'una variació aleatòria en la distribució d'al·lels d'una generació a l'altra.

En cap generació, no es podria triar cap bola d'un color determinat, és a dir, no tenen descendència. En aquest exemple, si no es selecciona cap bola vermella, el pot que representa la nova generació només conté descendència blava. Si això passa, l'al·lel vermell s'ha perdut de manera permanent a la població, mentre que l'al·lel blau restant s'ha fixat: totes les generacions futures són completament blaves. En poblacions petites, la fixació es pot produir en poques generacions.

En aquesta simulació, cada punt negre d'una bola significa que ha estat escollida per copiar (reproduir) una vegada. La fixació de l'"al·lel" blau es produeix en cinc generacions.

Probabilitat i freqüència de l'al·lel

Els mecanismes de la deriva genètica es poden il·lustrar amb un exemple simplificat. Es considera una colònia molt gran de bacteris aïllats en una gota de solució. Els bacteris són genèticament idèntics excepte un únic gen amb dos al·lels marcats A i B, que són al·lels neutres, és a dir, no afecten la capacitat del bacteri per sobreviure i reproduir-se; tots els bacteris d'aquesta colònia tenen la mateixa probabilitat de sobreviure i reproduir-se. Es suposa que la meitat dels bacteris tenen l'al·lel A i l'altra meitat tenen l'al·lel B. Així, A i B tenen cadascun una freqüència d'al·lel d'1/2.

Aleshores, la gota de solució es redueix fins que només té prou menjar per mantenir quatre bacteris. Tots els altres bacteris moren sense reproduir-se. Entre les quatre que sobreviuen, existeixen 16 combinacions possibles per als al·lels A i B:

(A-A-A-A), (B-A-A-A), (A-B-A-A), (B-B-A-A),
(A-A-B-A), (B-A-B-A), (A-B-B-A), (B-B-B-A),
(A-A-A-B), (B-A-A-B), (A-B-A-B), (B-B-A-B),
(A-A-B-B), (B-A-B-B), (A-B-B-B), (B-B-B-B).

Com que tots els bacteris de la solució original tenen la mateixa probabilitat de sobreviure quan la solució es redueix, els quatre supervivents són una mostra aleatòria de la colònia original. La probabilitat que cadascun dels quatre supervivents tingui un al·lel determinat és 1/2 i, per tant, la probabilitat que es produeixi una combinació d'al·lels en particular quan la solució es redueix és:

${\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1}{16}}.$

(La mida de la població original és tan gran que el mostreig es fa efectivament amb la substitució). En altres paraules, cada una de les 16 combinacions d'al·lels possibles és igual de probable que es produeixi, amb una probabilitat d'1/16.

Comptant les combinacions amb el mateix nombre d'A i B dona la següent taula:

A	B	Combinations	Probability
4	0	1	1/16
3	1	4	4/16
2	2	6	6/16
1	3	4	4/16
0	4	1	1/16

Com es mostra a la taula, el nombre total de combinacions que tenen el mateix nombre d'al·lels A que d'al·lels B és de sis, i la probabilitat d'aquesta combinació és de 6/16. El nombre total d'altres combinacions és deu, de manera que la probabilitat d'un nombre desigual d'al·lels A i B és 10/16. Així, tot i que la colònia original va començar amb un nombre igual d'al·lels A i B, és molt possible que el nombre d'al·lels de la població restant de quatre membres no sigui igual. La situació de nombres iguals és en realitat menys probable que de nombres desiguals. En aquest últim cas, la deriva genètica s'ha produït perquè les freqüències d'al·lels de la població han canviat a causa del mostreig aleatori. En aquest exemple, la població es va contreure amb només quatre supervivents aleatoris, un fenomen conegut com a coll d'ampolla de població.

Les probabilitats del nombre de còpies de l'al·lel A (o B) que sobreviuen (donades a l'última columna de la taula anterior) es poden calcular directament a partir de la distribució binomial, on la probabilitat d'"èxit" (probabilitat que un al·lel determinat estigui present) és 1/2 (és a dir, la probabilitat que hi hagi k còpies d'al·lels A (o B) a la combinació) ve donada per:

${n \choose k}\left({\frac {1}{2}}\right)^{k}\left(1-{\frac {1}{2}}\right)^{n-k}={n \choose k}\left({\frac {1}{2}}\right)^{n}\!$

on n=4 és el nombre de bacteris supervivents.

Models matemàtics

Els models matemàtics de la deriva genètica es poden dissenyar utilitzant processos de ramificació o una equació de difusió que descrigui els canvis en la freqüència d'al·lels en una població idealitzada.

Model Wright–Fisher

Si es considera un gen amb dos al·lels, A o B. En diploïdia, les poblacions formades per N individus tenen 2N còpies de cada gen. Un individu pot tenir dues còpies del mateix al·lel o dos al·lels diferents. La freqüència d'un al·lel s'assigna p i l'altre q. El model de Wright-Fisher (anomenat així per Sewall Wright i Ronald Fisher) suposa que les generacions no es superposen (per exemple, les plantes anuals tenen exactament una generació per any) i que cada còpia del gen que es troba a la nova generació es dibuixa de manera independent a l'atzar de totes les còpies del gen de l'antiga generació. La fórmula per calcular la probabilitat d'obtenir k còpies d'un al·lel que tingués freqüència p en l'última generació és llavors

${\frac {(2N)!}{k!(2N-k)!}}p^{k}q^{2N-k}$

on el símbol "!" significa la funció factorial. Aquesta expressió també es pot formular utilitzant el coeficient binomial,

${2N \choose k}p^{k}q^{2N-k}$

Model Moran

El model de Moran suposa generacions superposades. A cada pas de temps, s'escull un individu per reproduir-se i un individu per morir. Així, en cada pas de temps, el nombre de còpies d'un al·lel determinat pot augmentar un, baixar un o mantenir-se igual. Això vol dir que la matriu de transició és triagonal, el que significa que les solucions matemàtiques són més fàcils per al model de Moran que per al model de Wright-Fisher. D'altra banda, les simulacions per ordinador solen ser més fàcils de realitzar mitjançant el model Wright-Fisher, perquè cal calcular menys passos de temps. En el model de Moran, es necessiten N passos de temps per passar una generació, on N és la mida efectiva de la població. En el model Wright-Fisher, només se'n necessita un.

A la pràctica, els models Moran i Wright-Fisher donen resultats qualitativament similars, però la deriva genètica corre el doble de ràpid en el primer.

Altres models de deriva

Si la variància en el nombre de descendència és molt més gran que la donada per la distribució binomial assumida pel model de Wright-Fisher, aleshores donada la mateixa velocitat general de deriva genètica (la mida efectiva de la variància de la població), la deriva genètica és una força menys poderosa en comparació amb la selecció. Fins i tot per a la mateixa variància, si els moments més alts de la distribució del nombre de descendència superen els de la distribució binomial, de nou la força de la deriva genètica es debilita substancialment.

Efectes aleatoris diferents de l'error de mostreig

Els canvis aleatoris en les freqüències d'al·lel també poden ser causats per efectes diferents de l'error de mostreig, per exemple, canvis aleatoris en la pressió de selecció.

Una font alternativa important d'estocasticitat, potser més important que la deriva genètica, és l'esborrany genètic. L'esborrany genètic és l'efecte sobre un locus per selecció en locus enllaçats. Les propietats matemàtiques de l'esborrany genètic són diferents de les de la deriva genètica. La direcció del canvi aleatori en la freqüència d'al·lel està autocorrelacionada entre generacions.

Deriva i fixació

El principi de Hardy-Weinberg estableix que dins de poblacions prou grans, les freqüències d'al·lels romanen constants d'una generació a l'altra tret que l'equilibri es vegi alterat per migració, mutacions genètiques o selecció.

Tanmateix, en poblacions finites, no s'obtenen nous al·lels a partir del mostreig aleatori d'al·lels passats a la següent generació, però el mostreig pot fer que un al·lel existent desaparegui. Com que el mostreig aleatori pot eliminar, però no substituir, un al·lel, i perquè les disminucions o augments aleatoris de la freqüència d'al·lels influeixen en les distribucions d'al·lels esperades per a la propera generació, la deriva genètica condueix una població cap a la uniformitat genètica al llarg del temps. Quan un al·lel arriba a una freqüència d'1 (100%) es diu que està "fix" a la població i quan un al·lel arriba a una freqüència de 0 (0%) es perd. Les poblacions més petites aconsegueixen la fixació més ràpidament, mentre que en el límit d'una població infinita, la fixació no s'aconsegueix. Una vegada que un al·lel es fixa, la deriva genètica s'atura i la freqüència de l'al·lel no pot canviar tret que s'introdueix un nou al·lel a la població mitjançant mutació o flux genètic. Així, tot i que la deriva genètica és un procés aleatori i sense direcció, actua per eliminar la variació genètica al llarg del temps.

Taxa de canvi de freqüència al·lel a causa de la deriva

Deu simulacions de deriva genètica aleatòria d'un sol al·lel donat amb una distribució de freqüència inicial de 0,5 mesurada al llarg de 50 generacions, repetides en tres poblacions reproductivament sincròniques de diferents mides. En aquestes simulacions, els al·lels es desplacen cap a la pèrdua o la fixació (freqüència de 0,0 o 1,0) només a la població més petita.

Suposant que la deriva genètica és l'única força evolutiva que actua sobre un al·lel, després de t generacions en moltes poblacions replicades, començant per les freqüències d'al·lel de p i q, la variació de la freqüència d'al·lel entre aquestes poblacions és

$V_{t}\approx pq\left(1-\exp \left(-{\frac {t}{2N_{e}}}\right)\right)$

Temps de fixació o pèrdua

Suposant que la deriva genètica és l'única força evolutiva que actua sobre un al·lel, en un moment donat la probabilitat que un al·lel eventualment es fixi en la població és simplement la seva freqüència a la població en aquell moment. Per exemple, si la freqüència p de l'al·lel A és del 75% i la freqüència q de l'al·lel B és del 25%, aleshores, donat un temps il·limitat, la probabilitat que A finalment es fixi a la població és del 75% i la probabilitat que B es fixi és 25%.

El nombre esperat de generacions perquè es produeixi la fixació és proporcional a la mida de la població, de manera que es preveu que la fixació es produeixi molt més ràpidament en poblacions més petites. Normalment, la mida efectiva de la població, que és més petita que la població total, s'utilitza per determinar aquestes probabilitats. La població efectiva (N^e) té en compte factors com el nivell de consanguinitat, l'etapa del cicle de vida en què la població és la més petita i el fet que alguns gens neutres estan vinculats genèticament amb d'altres que estan en selecció. La mida efectiva de la població pot no ser la mateixa per a tots els gens de la mateixa població.

Una fórmula prospectiva utilitzada per aproximar el temps esperat abans que un al·lel neutre es fixi mitjançant la deriva genètica, segons el model de Wright-Fisher, és

${\bar {T}}_{\text{fixed}}={\frac {-4N_{e}(1-p)\ln(1-p)}{p}}$

on T és el nombre de generacions, N^e és la mida efectiva de la població i p és la freqüència inicial de l'al·lel donat. El resultat és el nombre de generacions que s'espera que passin abans que es produeixi la fixació d'un al·lel determinat en una població amb una mida (N^e) i una freqüència d'al·lel (p) determinades.

El temps esperat perquè l'al·lel neutre es perdi a causa de la deriva genètica es pot calcular com

${\bar {T}}_{\text{lost}}={\frac {-4N_{e}p}{1-p}}\ln p.$

Quan una mutació apareix només una vegada en una població prou gran perquè la freqüència inicial sigui insignificant, les fórmules es poden simplificar a

${\bar {T}}_{\text{fixed}}=4N_{e}$

per al nombre mitjà de generacions esperades abans de la fixació d'una mutació neutra, i

${\bar {T}}_{\text{lost}}=2\left({\frac {N_{e}}{N}}\right)\ln(2N)$

per al nombre mitjà de generacions esperades abans de la pèrdua d'una mutació neutra en una població de mida real N.

Temps fins a la pèrdua tant amb deriva com mutació

Les fórmules anteriors s'apliquen a un al·lel que ja està present en una població i que no està subjecte a mutació ni a la selecció natural. Si un al·lel es perd per mutació molt més sovint que no pas per mutació, aleshores la mutació, així com la deriva, poden influir en el temps fins a la pèrdua. Si l'al·lel propens a la pèrdua mutacional comença tal com està fixat a la població i es perd per mutació a una velocitat m per replicació, aleshores el temps esperat en generacions fins a la seva pèrdua en una població haploide ve donat per

${\bar {T}}_{\text{lost}}\approx {\begin{cases}{\dfrac {1}{m}},{\text{ if }}mN_{e}\ll 1\\[8pt]{\dfrac {\ln {(mN_{e})}+\gamma }{m}}{\text{ if }}mN_{e}\gg 1\end{cases}}$

on γ és la constant d'Euler. La primera aproximació representa el temps d'espera fins al primer mutant destinat a la pèrdua, amb una pèrdua que es produeix amb relativa rapidesa per deriva genètica, prenent un temps 1/m ≫ N^e. La segona aproximació representa el temps necessari per a la pèrdua determinista per acumulació de mutacions. En ambdós casos, el temps fins a la fixació està dominat per la mutació mitjançant el terme 1/m, i es veu menys afectat per la mida poblacional efectiva.

Contra la selecció natural

En les poblacions naturals, la deriva genètica i la selecció natural no actuen de manera aïllada; tots dos fenòmens estan sempre en joc, juntament amb la mutació i la migració. L'evolució neutral és el producte tant de la mutació com de la deriva, no només de la deriva. De la mateixa manera, fins i tot quan la selecció aclapara la deriva genètica, només pot actuar sobre la variació que proporciona la mutació.

Mentre que la selecció natural té una direcció, guiant l'evolució cap a adaptacions hereditàries a l'entorn actual, la deriva genètica no té cap direcció i només es guia per les matemàtiques de l'atzar. Com a resultat, la deriva actua sobre les freqüències genotípiques d'una població sense tenir en compte els seus efectes fenotípics. En canvi, la selecció afavoreix la propagació d'al·lels els efectes fenotípics dels quals augmenten la supervivència i/o la reproducció dels seus portadors, redueix les freqüències d'al·lels que causen trets desfavorables i ignora els que són neutres.

La llei dels grans nombres prediu que quan el nombre absolut de còpies de l'al·lel és petit (per exemple, en poblacions petites), la magnitud de la deriva de les freqüències d'al·lel per generació és més gran. La magnitud de la deriva és prou gran com per aclaparar la selecció a qualsevol freqüència d'al·lel quan el coeficient de selecció és inferior a 1 dividit per la mida efectiva de la població. Per tant, es considera que l'evolució no adaptativa resultant del producte de la mutació i la deriva genètica és un mecanisme conseqüent de canvi evolutiu principalment dins de poblacions petites i aïllades. Les matemàtiques de la deriva genètica depenen de la mida efectiva de la població, però no està clar com es relaciona això amb el nombre real d'individus en una població. L'enllaç genètic amb altres gens que estan en selecció pot reduir la mida efectiva de la població experimentada per un al·lel neutre. Amb una taxa de recombinació més alta, l'enllaç disminueix i amb això aquest efecte local sobre la mida efectiva de la població. Aquest efecte és visible a les dades moleculars com una correlació entre la taxa de recombinació local i la diversitat genètica, i una correlació negativa entre la densitat de gens i la diversitat a les regions d'ADN no codificants. L'estocasticitat associada amb l'enllaç amb altres gens que estan en selecció no és el mateix que l'error de mostreig, i de vegades es coneix com a esborrany genètic per distingir-lo de la deriva genètica.

La baixa freqüència d'al·lels fa que els al·lels siguin més vulnerables a ser eliminats per casualitat, fins i tot anul·lant la influència de la selecció natural. Per exemple, mentre que les mutacions desavantatges solen eliminar-se ràpidament dins de la població, les noves mutacions avantatjoses són gairebé tan vulnerables a la pèrdua per deriva genètica com les mutacions neutres. Fins que la freqüència d'al·lel de la mutació avantatjosa no arribi a un cert llindar, la deriva genètica no tindrà cap efecte.

Bibliografia

• Avers, Charlotte J. Process and Pattern in Evolution. Nova York: Oxford University Press, 1989. ISBN 0-19-505275-7. OCLC 17677554. 
• Barton, Nicholas H.; Briggs, Derek E.G.; Eisen, Jonathan A. [et al.].. Evolution. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press, 2007. ISBN 978-0-87969-684-9. OCLC 86090399. 
• Campbell, Neil A. Biology. 4a edició. Menlo Park, CA: Benjamin/Cummings Pub. Co., 1996 (Benjamin/Cummings Series in the Life Sciences). ISBN 0-8053-1940-9. OCLC 33333455. 
• Cavalli-Sforza, L. Luca; Menozzi, Paolo; Piazza, Alberto. The History and Geography of Human Genes. Abridged paperback. Princeton, N.J.: Princeton University Press, 1996. ISBN 0-691-02905-9. OCLC 35527063. 
• Ewens, Warren J. Mathematical Population Genetics I. Theoretical Introduction. 27. 2nd. Nova York: Springer-Verlag, 2004 (Interdisciplinary Applied Mathematics). ISBN 0-387-20191-2. OCLC 53231891. 
• Freeman, Scott; Herron, Jon C. Evolutionary Analysis. 4a edició. Upper Saddle River, NJ: Pearson Prentice Hall, 2007. ISBN 978-0-13-227584-2. OCLC 73502978. 
• Futuyma, Douglas. Evolutionary Biology. 3rd. Sunderland, MA: Sinauer Associates, 1998. ISBN 0-87893-189-9. OCLC 37560100. 
• Non-Neutral Evolution: Theories and Molecular Data. Nova York: Chapman & Hall, 1994. ISBN 0-412-05391-8. OCLC 29638235.  "Papers from a workshop sponsored by the Canadian Institute for Advanced Research."
• Hartl, Daniel L.; Clark, Andrew G. Principles of Population Genetics. 4a edició. Sunderland, MA: Sinauer Associates, 2007. ISBN 978-0-87893-308-2. OCLC 75087956. 
• Hedrick, Philip W. Genetics of Populations. 3rd. Boston, MA: Jones and Bartlett Publishers, 2005. ISBN 0-7637-4772-6. OCLC 56194719. 
• Hey, Jody. Systematics and the Origin of Species: On Ernst Mayr's 100th Anniversary. Washington, D.C.: National Academies Press, 2005. ISBN 978-0-309-09536-5. OCLC 70745851. 
• Howard, Daniel J.. Endless Forms: Species and Speciation. Nova York: Oxford University Press, 1998. ISBN 978-0-19-510901-6. OCLC 37545522. 
• Kimura, Motoo; Ohta, Tomoko. Theoretical Aspects of Population Genetics. 4. Princeton, NJ: Princeton University Press, 1971, p. 1–219 (Monographs in Population Biology). ISBN 0-691-08096-8. OCLC 299867647. 
• Larson, Edward J. Evolution: The Remarkable History of a Scientific Theory. 17. Nova York: Modern Library, 2004 (Modern Library Chronicles). ISBN 0-679-64288-9. OCLC 53483597. 
• Li, Wen-Hsiung; Graur, Dan. Fundamentals of Molecular Evolution. Sunderland, MA: Sinauer Associates, 1991. ISBN 0-87893-452-9. OCLC 22113526. 
• Lynch, Michael. The Origins of Genome Architecture. Sunderland, MA: Sinauer Associates, 2007. ISBN 978-0-87893-484-3. OCLC 77574049. 
• Miller, Geoffrey. The Mating Mind: How Sexual Choice Shaped the Evolution of Human Nature. Nova York: Doubleday, 2000. ISBN 0-385-49516-1. OCLC 43648482. 
• Sadava, David; Heller, H. Craig; Orians, Gordon H. [et al.].. Life: The Science of Biology. II: Evolution, Diversity and Ecology. 8th. Sunderland, MA; Gordonsville, VA: Sinauer Associates; W. H. Freeman and Company, 2008. ISBN 978-0-7167-7674-1. OCLC 71632224. 
• Stevenson, Joan C. Dictionary of Concepts in Physical Anthropology. 10. Westport, CT: Greenwood Press, 1991 (Reference Sources for the Social Sciences and Humanities). ISBN 0-313-24756-0. OCLC 22732327. 
• Tian, Jianjun Paul. Evolution Algebras and their Applications. 1921. Berlin; New York: Springer, 2008 (Lecture Notes in Mathematics). DOI 10.1007/978-3-540-74284-5. ISBN 978-3-540-74283-8. OCLC 173807298. 
• Wolf, Jason B.. Epistasis and the Evolutionary Process. Oxford, UK; New York: Oxford University Press, 2000. ISBN 0-19-512806-0. OCLC 42603105. 
• Zimmer, Carl. Evolution: The Triumph of an Idea. Introduction by Stephen Jay Gould; foreword by Richard Hutton. 1st. Nova York: HarperCollins, 2001. ISBN 0-06-019906-7. OCLC 46359440.