Vés al contingut

Escala de distàncies còsmiques

De la Viquipèdia, l'enciclopèdia lliure
(S'ha redirigit des de: Escala de la distància còsmica)

L'escala de distàncies còsmiques són els diferents mètodes amb els quals els astrònoms determinen les distàncies als objectes celestes.[1] Una mesura directa de la distància a un objecte astronòmic només és possible en una escala relativament petita (en termes astronòmics). L'analogia de l'escala ix del fet segons el qual no hi ha una tècnica que puga mesurar distàncies en tots els rangs que es troben en astronomia. D'aquesta manera, es pot usar un mètode per amidar les distàncies pròximes, un altre per amidar distàncies que van de la proximitat a distàncies mitjanes, i així successivament. Cada graó de l'escala dona informació que pot ser usada per a determinar les distàncies en el pròxim graó més alt.

Distàncies fonamentals

[modifica]

A la base de l'escala, hi trobam la mida de les distàncies fonamentals, en la qual les distàncies són determinades directament, sense suposicions físiques sobre la natura de l'objecte en qüestió. Aquestes distàncies fonamentals es basen en la geometria, o en el temps en què viatge la llum (és a dir, la constància de la celeritat de la llum), així com en el radar.

El primer esglaó de veritat de l'escala, la base de totes les distàncies astronòmiques és el radi de l'òrbita de la Terra (la distància entre la Terra i el Sol), anomenada unitat astronòmica (UA).[2][3] Les altres distàncies astronòmiques es construeixen a partir d'aquesta. Històricament, l'observació del trànsit de Venus[4] fou crucial per determinar la UA; a la primera meitat del segle xx, les observacions d'asteroides varen ser també importants.

En el present, la UA es determina amb molta precisió usant les mesures amb radar[5] de Venus i altres planetes i asteroides pròxims,[6] i el rastreig de les naus espacials interplanetàries en les seves òrbites voltant el Sol a través del sistema solar. Les lleis de Kepler del moviment planetari ens donen una proporció precisa de les diferents òrbites dels objectes que volten el Sol, però no una mesura real de les òrbites mateixes. El radar ens dona un valor en quilòmetres de la diferència entre dues òrbites, i a partir d'això la proporció entre les dues, i d'aquestes es pot deduir directament l'òrbita de la Terra.[7]

El radar només es pot usar dins el sistema solar i aquestes distàncies fonamentals provenen de la trigonometria i de mesures precises dels angles, similars a l'agrimensura. La mesura precisa de les posicions estel·lars és una part de la disciplina anomenada astrometria.[8]

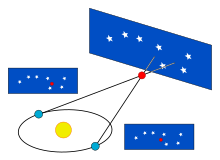
Un estel proper sembla que canviï de posició respecte als estels llunyans, segons el recorregut de la Terra per la seva òrbita.

La mida de les distàncies fonamentals més importants prové de la paral·laxi. El moviment de la Terra voltant el Sol causa petits canvis de la posició de les estrelles. Aquests canvis són angles (la meitat de l'angle total) d'un triangle rectangle, d'1 ua de catet del triangle i la distància a l'estrella la hipotenusa. Un parsec és la distància d'una estrella que té una paral·laxi d'1 segon d'arc. Els astrònoms, usualment, expressen les distàncies en parsecs; en canvi, els anys llum s'usen en els medis populars, però gairebé tots els valors en anys llum han estat convertits de nombres tabulats en parsecs en la font original.

Com que la paral·laxi esdevé molt petita per a les distàncies grans, usualment només es poden mesurar les distàncies de les estrelles que tenen una paral·laxi que no superi la precisió del mesurament. A la dècada a partir del 1990, la missió Hipparcos obtingué la paral·laxi de més de cent mil estrelles amb una precisió d'una mil·lèsima de segon d'arc, la qual cosa va fornir les distàncies usuals d'estrelles a uns pocs centenars de parsecs.[9]

Un altre mètode fonamental per a mesurar les distàncies és la paral·laxi secular i estadística.[10] Aquesta tècnica combina el mesurament dels moviments i l'esclat dels membres d'un grup homogeni seleccionat d'estrelles de manera estadística per deduir una distància mitjana per a tot el grup. Aquest mètode ha esdevingut una tècnica importat per a les cefeides i les variables RR Lyrae.

La paral·laxi dinàmica de cúmuls[11] és una tècnica en la qual els moviments d'estrelles individuals en un cúmul estel·lar pròxim (només els cúmuls oberts estan prou a prop perquè aquesta tècnica sigui útil) pot ser usada per a trobar la distància al cúmul. En particular, la distància obtinguda per les Híades ha estat un pas importat en l'escala de les distàncies.

Altres objectes individuals poder tenir estimacions fonamentals de la distància fetes en circumstàncies especials. Si l'expansió d'un núvols de gas, com en el romanent d'una supernova o una nebulosa planetària, poden ser observats durant un temps, llavors es pot estimar una distància segons la paral·laxi d'expansió. Les estrelles binàries que són visuals i espectroscòpiques poden tenir la seva distància estimada per mitjans similars. La característica comuna n'és que un mesurament del moviment angular es combina amb un mesurament de la velocitat absoluta (usualment, obtinguda per efecte Doppler). La distància estimada prové de calcular com de lluny ha d'estar l'objecte perquè la seva velocitat absoluta aparegui amb el moviment angular observat.

La paral·laxi d'expansió en particular pot donar estimacions fonamentals de la distància per a objectes molt allunyats, ja que el material expulsat per una supernova té una velocitat d'expansió i pot ser de molta magnitud (comparat amb les estrelles). Més endavant, poden ser observades per interferometria de ràdio que pot amidar moviments angulars molt petits. Això porta que algunes supernoves en altres galàxies tenen estimacions de distàncies fonamentals.[12] Encara que valuosos, aquests casos són molt rars, encara que donen una prova important de consistència de l'esglaó de la distància com si fossin cent cavalls de força per si mateixos.

Distàncies físiques

[modifica]

Amb algunes excepcions, les distàncies fonamentals estan disponibles només fins a alguns milers de parsecs, la qual cosa és només una modesta porció de la nostra pròpia galàxia. Per a distàncies que vagin més enllà d'això, les mides depenen de presumpcions físiques, això és, l'asseveració que un reconeix l'objecte en qüestió, i la classe d'objectes és a bastament homogeni perquè els seus membres puguin ser usats amb estimació significativa de la distància.

Quasi tots aquests indicadors de distàncies físiques són candeles canòniques. Aquest testimoni de reconèixer un objecte com a pertanyent a una classe, la qual té una magnitud absoluta coneguda, amidant la seva magnitud aparent, i usant la llei de l'invers del quadrat per a inferir la distància que es necessita per a fer que la candela sembli com ha estat observada. Qualque mitjà de comptar per extinció interestel·lar, que fa aparèixer els objectes més febles, també és necessari. La diferència entre magnitud absoluta i aparent s'anomena mòdul de distància, i les distàncies astronòmiques, especialment les intergalàctiques, estan a vegades tabulades d'aquesta manera.

Els indicadors de distància, usats de manera progressiva per a escales de distàncies cada vegada més llargues, són:

Per a qualsevol candela canònica hi ha dos problemes. El principal és el calibratge, determinar exactament quina és la magnitud absoluta de la candela. Això inclou definir la classe a bastament perquè els membres puguin ser reconeguts, i trobar membres a bastament amb distàncies ben conegudes perquè la seva magnitud absoluta pugui ser determinada força acuradament. El segon consisteix a reconèixer els membres de cada classe, i no equivocar-se usant el calibratge de les candeles canòniques sobre un objecte que no pertanyi a la classe en qüestió. A distàncies extremes, qualsevol voldria usar un indicador de distància, aquest problema de reconeixement pot ser molt seriós.

(Una altra classe d'indicador de distància física és la regla canònica, però actualment s'usa molt poc.)

Una successió d'indicadors de distància, que és una escala de distàncies, es necessita per a determinar les distàncies a altres galàxies, ja que els objectes brillants que puguin ser reconeguts i mesurats a tals distàncies són molt rars i només se'n poden trobar molt pocs, o cap, de manera que són pocs exemples per a poder calibrar-ne l'indicador per paral·laxi trigonomètrica. Per exemple, les variables cefeides són un dels millors indicadors en el cas de les galàxies espirals, que no es poden calibrar només per paral·laxi. També s'ha d'esmentar que les diferents poblacions estel·lars, generalment, no tenen tots els tipus d'estrelles. Les cefeides en particular són estrelles massives, amb una vida curta; per tant, només es poden trobar en llocs on les estrelles s'han format recentment. Consegüentment, com que les galàxies el·líptiques usualment fa temps que han cessat de formar estrelles de gran escala, ja no tenen cefeides. Per tant, s'hi han d'usar els indicadors de distància basats en la població estel·lar vella (com poden ser les novae i RR Lyrae variables). Sigui com sigui, les vaiables RR Lyrae són menys lluminoses que les cefeides; per tant, no es poden veure de tan lluny com les cefeides, i les novae són impredictibles i es necessita un programa intensiu d'intercepció —i sort durant el programa— de les novae dins la galàxia objecte d'estudi per a una bona estimació de la distància.

Com que els esglaons més distants de l'escala de la distància còsmica depenen dels més pròxims, els passos més distants inclouen els efectes dels errors en els passos més pròxims, sistemàtics i estadístics. El resultat d'aquesta propagació d'errors significa que la distància en astronomia és coneguda rarament amb el mateix nivell de precisió que les mides en altres ciències, i aquesta precisió necessàriament és més pobra per als tipus d'objectes més distants.

També s'ha de fer una observació especialment en relació amb les candeles canòniques més brillants, és la seva canonicitat: en quina mesura són homogenis aquests objectes i si ho és la seva magnitud absoluta. En el cas de qualcunes de les diferents candeles canòniques, la seva homogeneïtat es basa en teories sobre la formació i evolució de les estrelles i galàxies, i això, doncs, està també subjecte a incerteses en aquests darrers aspectes. En la major part dels més lluminosos indicadors de distància, el tipus Ia supernovae, aquesta homogeneïtat se sap que és pobra; sigui com sigui, no hi ha una altra classe d'objectes amb esclat suficient perquè siguin detectats a tan llarga distància; per tant, no n'hi ha altra alternativa.

L'observació de la llei de Hubble, la relació proporcional entre la distància i la velocitat en què una galàxia s'allunya (usualment, esmentat com a desplaçament cap al roig) és un producte de l'escala de les distàncies còsmiques. Hubble observà que les galàxies més febles tenien elevades velocitats de recessió. Trobar el valor de la constant de Hubble ha estat el resultat de dècades de treball per a molts astrònoms, tant en l'avaluació de la mesura del desplaçament cap al roig de les galàxies com en el calibratge dels esglaons de l'escala de distàncies. La llei de Hubble és l'únic mitjà de què disposam per a estimar la distància de la majoria de quàsars i altres galàxies distants en els quals els indicadors de distàncies individuals no es poden veure.

Notes

[modifica]
  1. ↑ Webb, S. Measuring the Universe: The Cosmological Distance Ladder. Springer, 1999 (Space Exploration). ISBN 978-1-85233-106-1. 
  2. ↑ McCarthy, D.D.; Seidelmann, P.K.. Time: From Earth Rotation to Atomic Physics. Cambridge University Press, 2018, p. 41. ISBN 978-1-107-19728-2. 
  3. ↑ Bely, P.Y.; Christian, C.; Roy, J.R.. 250 réponses à vos questions sur l'astronomie (en francès). Éditions du Gerfaut, 2008, p. 24 (250 réponses). ISBN 978-2-35191-012-2. 
  4. ↑ Rothen, F. Surprenante gravité (en francès). Presses polytechniques et universitaires romandes, 2009, p. 219 (Collection Focus science). ISBN 978-2-88074-774-9. 
  5. ↑ Tatarewicz, J.N.. Space Technology & Planetary Astronomy. Indiana University Press, 1990, p. 16 (Science, technology, and society). ISBN 978-0-253-35655-0. 
  6. ↑ Ash, M.E., Shapiro, I.I., & Smith, W.B., 1967 Astronomical Journal, 72, 338-350.
  7. ↑ Descamps, P. 24 heures dans la vie des étoiles (en francès). La Librairie Vuibert, 2019, p. 122. ISBN 978-2-311-10287-1. 
  8. ↑ Kovalevsky, J.; Seidelmann, P.K.. Fundamentals of Astrometry. Cambridge University Press, 2004. ISBN 978-1-139-45317-2. 
  9. ↑ Metchev, S. Brown Dwarf Companions to Young Solar an. Universal Publishers, 2006, p. 23. ISBN 978-1-58112-290-9. 
  10. ↑ Binney, J.; Merrifield, M. Galactic Astronomy. Princeton University Press, 2021, p. 46 (Princeton Series in Astrophysics). ISBN 978-0-691-23332-1. 
  11. ↑ Webb, S. Measuring the Universe: The Cosmological Distance Ladder. Springer, 1999, p. 70 (Space Exploration). ISBN 978-1-85233-106-1. 
  12. ↑ Bartel, N., i cols., 1994, "The shape, expansion rate and distance of supernova 1993J from VLBI measurements", Nature 368, 610-613

Enllaços externs

[modifica]
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Escala_de_distàncies_còsmiques&oldid=32829299»