Unitat astronòmica
| Per a altres significats, vegeu «UA (desambiguació)». |
 | |
| Tipus | unitat de longitud, unitat no SI acceptada pel SI, unitat derivada en UCUM i unitats que no formen part del SI però s'hi mencionen i accepten |
|---|---|
| Sistema d'unitats | Sistema astronòmic d'unitats (acceptat per l'ús al SI) |
| Unitat de | Longitud |
| Símbol | UA |
| Conversions d'unitats | |
| Unitats mètriques (SI) | 1,4960×1011 m |
| Unitats imperials | 9,2956×107 mi |
| Unitats astronòmiques | 4,8481×10−6 pc 1,5813×10−5 anys llum |
| A unitats del SI | 149.597.870.700 m |
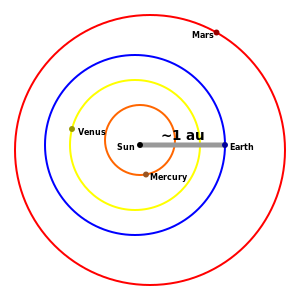
La unitat astronòmica (símbol ua[1] o, en anglès, au;[2] de vegades també UA[3] o AU)[4] és una unitat de longitud del sistema astronòmic que correspon aproximadament a la distància que separa la Terra del Sol. Actualment es defineix la unitat astronòmica exactament com a 149 597 870 700 m (aproximadament 150 × 10⁶ km).[5] Aquesta definició fou adoptada per la Unió Astronòmica Internacional l'any 2012 i és lleugerament menor que la distància mitjana de la Terra al Sol.[6]
La distància Terra-Sol varia segons l'òrbita de la Terra al voltant del Sol, des del màxim (afeli) fins al mínim (periheli) i de nou fins al màxim en el període d'un any. Originalment, cada distància fou mesurada mitjançant l'observació, i l'ua fou definida com la mitjana aritmètica de les distàncies (la semisuma de la màxima i la mínima), cosa que convertia la unitat astronòmica en una mena de mesura mitjana de la distància Terra-Sol.
Història
[modifica]
Mètode de la dicotomia lunar
[modifica]Aristarc de Samos (ca.310 aC - 230 aC) per estimar la distància Terra-Sol utilitzà el mètode de la dicotomia lunar, això és quan la Lluna s'observa exactament amb la meitat de la seva superfície il·luminada i l'altra fosca. En aquesta mitja lluna, l'astrònom mesura l'angle Lluna-Terra-Sol (). La distància Sol-Terra és llavors igual a la recíproca de vegades la distància Terra-Lluna . Aristarc mesurà que = 87° i, per tant, la distància Terra-Sol, en funció del radi de la Terra fou , equivalent a 0,049 ua actuals (error d'un –95,1 %).[7]
Malauradament aquest mètode té molts d'errors. En primer lloc, és extremadament difícil estimar el moment exacte de la dicotomia a causa de la naturalesa muntanyosa de la Lluna que fa que la frontera estigui lluny de ser lineal i també hi ha el problema que l'angle requerit, , va canviant ràpidament. Per altra banda, el fet que s'empri una funció cosinus en el càlcul significa que la diferència entre = 87° i = 89,333° (el valor correcte) introdueix un error d'un factor divuit.[7]
Hiparc de Nicea (ca 190 aC - ca 120 aC) utilitzà un enfocament que depenia del moment de les fases dels eclipsis lunars, i aquest temps conduí a un valor per a la paral·laxi horitzontal lunar (és a dir, la distància Terra-Lluna en termes del radi de la Terra). Combinant-ho amb l'acceptació de l'obra d'Aristarc que el Sol estava 19 vegades més lluny de la Terra que la Lluna (i així que la paral·laxi solar era 1/19 la paral·laxi lunar), va fer que la paral·laxi solar () fos una mica menys de 3', una xifra que fou acceptada per Claudi Ptolemeu (ca. 85 - ca. 165). Hiparc, però, es va adonar que 2'54" era probablement un límit superior. També assenyalà que el valor correcte no era observable en aquell moment i fins i tot podria ser tan baix com zero.[7]
Mètode de la paral·laxi geocèntrica
[modifica]
Un mètode millor, el de la paral·laxi diürna o geocèntrica (angle entre la direcció en què s'observa un astre des del centre de la Terra o direcció geocèntrica, i la direcció en què s'observa des d'un punt sobre la superfície de la Terra o direcció topocèntrica),[8] pogué aplicar-se després que Johannes Kepler (1571-1630) descobrís la seva 3a llei o llei harmònica (els quadrats dels períodes orbitals dels planetes són proporcionals als seus semieixos majors al cub). Segons aquesta llei, es coneixen les distàncies relatives dels planetes al Sol perquè estan relacionades amb els seus períodes orbitals que es poden mesurar fàcilment, i la distància del Sol a la Terra es pot prendre com la unitat de longitud. El mesurament de la distància de qualsevol planeta determinarà el valor d'aquesta unitat. Com més petita sigui la distància del planeta a la Terra, més grans seran els desplaçaments paral·làctics a mesurar, amb el corresponent augment de la precisió de la paral·laxi donada. Per tant, les condicions més favorables són proporcionades per l'observació, prop del moment d'oposició, dels planetes que s'acosten a la Terra. La determinació es pot basar en observacions simultànies o gairebé simultànies des de dos llocs diferents de la superfície terrestre agafant la seva distància com a línia base; o en observacions fetes després de la posta del sol i abans de l'alba en el mateix lloc, quan el desplaçament del lloc d'observació produït per la rotació de la Terra proporciona la línia de base per a les mesures.[9]
A partir de la paral·laxi de Mart
[modifica]Les primeres mesures serioses mitjançant la paral·laxi geocèntrica foren dutes a terme el 1672 per l'equip francès de Giovanni Domenico Cassini (1625-1712), Ole Rømer (1644-1710), Jean Richer (1630-1696) i Jean Picard (1620-1682). Van observar Mart a l'oposició (quan està a uns 0,38 ua de la Terra) tant de París com de Caiena, Guaiana Francesa. Cassini analitzà les observacions i obtingué un valor de π = 9,5'' per a la paral·laxi solar (angle sota el qual s'observaria el radi equatorial de la Terra des del centre del Sol),[10] i una distància Terra-Sol de , equivalent a 0,920 ua (error d'un –8 %). A partir de la paral·laxi geocèntrica de Mart i coneixent el diàmetre de la Terra, una simple relació trigonomètrica permet calcular la distància Terra-Mart . Per calcular la distància Sol-Terra s'ha d'emprar la distància Sol-Mart en funció de l'obtinguda amb la paral·laxi de Mart: i aplicar la relació de la 3a llei de Kepler amb els períodes en anys:
John Flamsteed (1646-1719) obtingué π = 10" (), Jean Picard π = 29" () i Lahire inferior a π < 6" (), de manera que la incertesa continuà. Flamsteed (1672) també observà Mart, el 1672, i va obtenir una paral·laxi marciana de 25" i una paral·laxi solar de π = 10". Isaac Newton, que era molt reticent a acceptar els valors francesos, tampoc estava massa content amb el de Flamsteed. L'efecte de la refracció atmosfèrica era greu, i la majoria dels astrònoms consideraven la similitud dels resultats de la paral·laxi solar com una mica fortuïta. Newton utilitzà un valor de π = 20" () en la primera edició dels Principia de 1687, però en la segona edició (publicada el 1713) donà el valor de Cassini i Kamsteed de π = 10" (). Aquesta meitat de la paral·laxi va portar, entre altres coses, a un augment de la massa acceptada del Sol per un factor de vuit. En la tercera edició de Principia (1726), Newton emprà π = 11", 12", i 13" en diferents llocs. Mentrestant, en la segona edició d'Optics (1717), utilitzà π = 12" ().[7]
A partir del trànsit de Venus
[modifica]
L'astrònom anglès Edmond Halley (1656-1742) s'allotjava a l'illa de Santa Helena el 1677 i estava recopilant el seu catàleg estel·lar de l'hemisferi sud quan observà el trànsit de Mercuri el 28 d'octubre de 1677. Mesurà una durada del trànsit de 5 h 14 m 20 s i determinà la durada teòrica del trànsit respecte al centre terrestre utilitzant les taules astronòmiques de l'astrònom anglès Thomas Streete (1622-1689). A partir de la ràtio d'aquests valors i dels valors sobre els quals es basaven les taules, Halley calculà la paral·laxi solar obtenint π = 45". L'error era considerable, però pensà que podria emprar el mateix mètode amb els trànsits de Venus que tendria menys error. Per això dirigí una crida a les futures generacions d'astrònoms per utilitzar els trànsits de Venus de 1761 i 1769 per a la determinació de la paral·laxi solar.[11]
Els trànsits de Venus de 1761 i 1769 donaren lloc a les primeres campanyes d'observació global amb participació internacional. Es feren enormes esforços, fins aleshores incomparables, per enviar expedicions a regions llunyanes i poc conegudes amb la tasca de mesurar els instants dels contactes interns i externs de Venus en el trànsit. El motiu d'aquest immens esforç fou que la determinació del valor de la paral·laxi solar amb alta precisió era important per a la ciència i per millorar la navegació. En aquells temps la navegació al mar es feia mesurant les distàncies lunars, és a dir, les distàncies angulars entre la Lluna i les estrelles. Els angles observats es comparaven amb els valors de taules astronòmiques i les diferències eren una mesura per a les longituds geogràfiques. Les taules astronòmiques s'elaboraven amb teories sobre els moviments de Sol i Lluna que es basen en la paral·laxi solar, per la qual cosa depenia implícitament d'aquesta important constant. Conèixer-la i utilitzar la tercera llei de Kepler també permetia determinar les dimensions del sistema solar, és a dir, totes les distàncies entre els cossos del sistema solar, la qual cosa tenia una gran importància científica.[11]
Per al trànsit de 1761 s'organitzaren vuit expedicions amb participació de nou nacions sota el lideratge de la França de Lluís XV. Es feren observacions en més de seixanta-dues estacions per part de més de cent vint observadors. Els resultats dels càlculs de diferents autors donaren un valor mitjà de π = 9,40" ± 0,72". Les observacions del trànsit del 1769 foren liderades per la Gran Bretanya de Jordi III. Hi participaren vuit nacions amb més de cent cinquanta observadors a més de setanta-set estacions i s'organitzaren deu expedicions, de les quals en destaca el primer viatge de James Cook (1728-1779) que no aconseguí bons resultats. Malgrat que molts dels resultats no foren precisos, el 1770 Leonhard Euler (1707-1783) publicà un treball sobre observacions d'aquest trànsit i conclogué que el valor de la paral·laxi solar era π = 8,80".[11] El valor admès en l'actualitat és π = 8,794148", que correspon a una distància mitjana al Sol de 149 597 870,61 km.
A partir de la paral·laxi d'Eros
[modifica]
El 3 d'agost de 1898 l'astrònom alemany Carl Gustav Witt (1866-1946) de l'Observatori d'Urania de Berlín, descobrí fotogràficament l'asteroide Eros, fet que captà enormement l'interès del món astronòmic, ja que era un candidat ideal per a mesures de la paral·laxi solar. Eros completa la seva òrbita al voltant del Sol en uns 643 dies, període que el situa a una distància del Sol inferior a la de Mart, variant entre 1,13 i 1,80 ua. Periòdicament s'apropa molt al nostre planeta, de vegades a només 23 × 10⁶ km, una mica més de la meitat de la distància mínima a Venus. Aviat s'organitzà una campanya per a l'observació durant el 1901 a la reunió de la Conférence Astrographique Internationale a París el juliol de 1900. Noves observacions d'Eros es feren el 1912 i el 1917. A finals de gener de 1931, es presentà una altra oportunitat amb Eros acostant-se a la Terra a 26 × 10⁶ km, molt favorable per a l'observació, particularment per als observatoris de l'hemisferi sud. La Unió Astronòmica internacional creà una comissió a càrrec de l'astrònom anglès Harold Spencer Jones (1890-1960).[12] El càlcul de la distància mitjana de la Terra al Sol, utilitzant els resultats de la campanya fou fet per Jones, que el 1941 donà com a resultat 1 ua = 149 674 000 ± 17 000 km.[13]
Mètode del temps d'eco de radar
[modifica]
També s'utilitzaren mètodes emprant la velocitat de la llum per determinar la paral·laxi solar. El valor de la velocitat de la llum s'ha determinat amb una precisió molt alta i es pot utilitzar de diverses maneres diferents. Un mètode directe és el contrari del procediment d'Ole Rømer en el descobriment de la velocitat de la llum; és a dir, utilitzar l'equació de la llum, o el temps que triga la llum a arribar-nos a les diferents distàncies de Júpiter, però la gran precisió difícilment es pot obtenir d'aquesta manera. Un segon mètode és mitjançant la constant d'aberració, que dona la relació de la velocitat de la Terra en la seva òrbita i la velocitat de la llum. Com que l'aberració produeix un termini anual d'amplitud de 20,496" en les posicions de totes les estrelles, la seva quantitat s'ha determinat de moltes maneres. Les observacions fetes a l'Observatori de Greenwich en els anys 1911 a 1936 donaren el valor de 20,489" ± 0,003" que van conduir al valor π = 8,797" ± 0,013" per a la paral·laxi solar.[14]
Les velocitats de les estrelles cap a o fora de la Terra es determinen a partir d'observacions espectroscòpiques. En triar els temps en què el moviment orbital de la Terra el porta cap a o des d'una estrella, els astrònoms són capaços de determinar matemàticament la velocitat de la Terra en la seva òrbita. D'aquesta manera es determinà la paral·laxi solar a partir d'observacions al Cap de Bona Esperança de ser de 8,802" ± 0,004".[14]
Les mesures mitjançant ecos de radar de la distància de la Terra-Venus han proporcionat la millor determinació de la paral·laxi solar. En mesurar el temps que necessita un pols de radar per viatjar fins a Venus, reflectir-se i tornar a la Terra, es pot obtenir la distància entre els dos planetes, ja que es coneix amb la màxima precisió la velocitat de la llum (c = 299 792 458 m/s), permetent la determinació de la distància entre la Terra i el Sol. Les principals limitacions d'utilitzar radar per mesurar la unitat astronòmica són la dependència del coneixement de les òrbites planetàries i la possibilitat d'efectes electromagnètics en el plasma Terra-Venus retardant el pols del radar.[14] Les mesures s'iniciaren durant la dècada de 1950 i alguns dels resultats obtinguts el 1961 foren: amb el radar Millstone del MIT 1 ua = 149 597 850 ± 400 km (freqüència 400 MHz, paral·laxi solar π = 8,794491" ± 0,000024" i radi equatorial de la Terra = 6 378,388 km) i amb el Goldstone del JPL 1 ua = 149 598 500 ± 500 km.[13]
Referències
[modifica]- ↑ Bureau International des Poids et Mesures. The International System of Units (SI). 8a ed.. Organisation Intergouvernementale de la Convention du Mètre, 2006, p. 126.
- ↑ RESOLUTION B2 on the re-definition of the astronomical unit of length. International Astronomical Union, 31 agost 2012. «The XXVIII General Assembly of International Astronomical Union … recommends … 5. that the unique symbol "au" be used for the astronomical unit.»
- ↑ «UA». Gran Diccionari de la Llengua Catalana. Barcelona: Grup Enciclopèdia Catalana.
- ↑ Linton, Christopher. From Eudoxus to Einstein : a history of mathematical astronomy. Nova York: Cambridge University Press, 2004, p. 359. ISBN 978-0-521-82750-8.
- ↑ RESOLUTION B2. International Astronomical Union, 31 agost 2012. «The XXVIII General Assembly of International Astronomical Union recommends [adopted] that the astronomical unit be re-defined to be a conventional unit of length equal to exactly 149,597,870,700 meters, in agreement with the value adopted in IAU 2009 Resolution B2»
- ↑ «Diccionari de física | TERMCAT». [Consulta: 14 maig 2021].
- ↑ 7,0 7,1 7,2 7,3 Hughes, David W. «Six stages in the history of the astronomical unit» (en anglès). Journal of Astronomical History and Heritage, 4, 1, 2001-06-XX, pàg. 15-28. ISSN: 1440-2807.
- ↑ Diccionario de astronomía. 1. ed. Madrid: Complutense, 1999. ISBN 84-89784-70-1.
- ↑ «Parallax - Solar parallax» (en anglès). [Consulta: 12 maig 2021].
- ↑ Bhatnagar, A. Fundamentals of solar astronomy. Hackensack, NJ: World Scientific, 2005. ISBN 981-256-787-9.
- ↑ 11,0 11,1 11,2 Verdun, A. «The Determination of the Solar Parallax from Transits of Venus in the 18th Century». Archives des sciences et compte rendu des séances de la Société / édités par la Société de physique et d'histoire naturelle de Genève, 57, 1, 10-2004, pàg. 45-68.
- ↑ «Eros y la determinación de la paralaje solar desde Argentina» (en castellà), 30-01-2012. [Consulta: 14 maig 2021].
- ↑ 13,0 13,1 Pettingill, G. H.; Briscoe, H. W.; Evans, J. V.; Gehrels, E.; Hyde, G. M. «A radar investigation of Venus». The Astronomical Journal, 67, 1962-05-XX, pàg. 181. DOI: 10.1086/108692.
- ↑ 14,0 14,1 14,2 «Parallax» (en anglès). Encyclopædia Britannica, 2003.















![{\displaystyle {\frac {r_{ST}^{3}}{r_{SM}^{3}}}={\frac {T_{T}^{2}}{T_{M}^{2}}}\quad \longrightarrow \quad {\frac {r_{ST}}{r_{ST}+r_{TM}}}={\sqrt[{3}]{\frac {1^{2}}{1.88^{2}}}}\quad \longrightarrow \quad r_{ST}={\frac {0,6565\;r_{TM}}{0,3435}}=1,911\;r_{TM}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe04c70dfd964b32e7c2a32068d2da1d956d13b)






