Formulació d'espai de fases

Funció de Wigner per als estats numèrics a) n = 0, b) n = 1 i c) n = 19. Les distribucions marginals de x i p es recuperen integrant sobre p i x respectivament.

La formulació de l'espai de fases de la mecànica quàntica situa les variables de posició i moment en peu d'igualtat a l'espai de fases. En canvi, la imatge de Schrödinger utilitza les representacions de posició o moment (vegeu també espai de posició i moment). Les dues característiques clau de la formulació de l'espai de fases són que l'estat quàntic es descriu mitjançant una distribució de quasiprobabilitat (en lloc d'una funció d'ona, un vector d'estat o una matriu de densitat) i la multiplicació de l'operador es substitueix per un producte estrella.

La teoria va ser desenvolupada completament per Hilbrand Groenewold el 1946 en la seva tesi doctoral, i de manera independent per Joe Moyal, basant-se cadascuna en idees anteriors d'Hermann Weyl i Eugene Wigner.

El principal avantatge de la formulació de l'espai de fases és que fa que la mecànica quàntica sembli tan semblant a la mecànica hamiltoniana com sigui possible evitant el formalisme de l'operador, "alliberant" així la quantificació de la "càrrega" de l'espai de Hilbert". Aquesta formulació és de naturalesa estadística i ofereix connexions lògiques entre la mecànica quàntica i la mecànica estadística clàssica, permetent una comparació natural entre ambdues (vegeu el límit clàssic). La mecànica quàntica a l'espai de fases és sovint afavorida en determinades aplicacions d'òptica quàntica (vegeu l'espai de fase òptic), o en l'estudi de la decoherència i una sèrie de problemes tècnics especialitzats, encara que, en cas contrari, el formalisme s'utilitza amb menys freqüència en situacions pràctiques.

Les idees conceptuals subjacents al desenvolupament de la mecànica quàntica a l'espai de fases s'han ramificat en derivacions matemàtiques com la deformació-quantització de Kontsevich (vegeu la fórmula de quantificació de Kontsevich) i la geometria no commutativa.

Evolució temporal de la funció Wigner combinada de terra i 1r estat excitat per a l'oscil·lador harmònic simple. Observeu el moviment rígid a l'espai de fases corresponent a les oscil·lacions convencionals a l'espai de coordenades.

Funció de Wigner per a l'estat fonamental de l'oscil·lador harmònic, desplaçat de l'origen de l'espai de fase, és a dir, un estat coherent. Observeu la rotació rígida, idèntica al moviment clàssic: aquesta és una característica especial del SHO, que il·lustra el principi de correspondència.

La funció de Wigner evolució temporal del potencial de Morse U(x) = 20(1 − e−0,16x)2 en unitats atòmiques (a.u.). Les línies sòlides representen el conjunt de nivells de l'Hamiltonià H(x, p) = p2/2 + U(x).

Distribució fase-espai

La distribució de fase-espai f(x, p) d'un estat quàntic és una distribució de quasiprobabilitat. En la formulació de l'espai fase, la distribució de l'espai fase es pot tractar com la descripció primitiva fonamental del sistema quàntic, sense cap referència a les funcions d'ona o matrius de densitat.

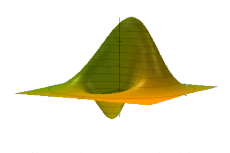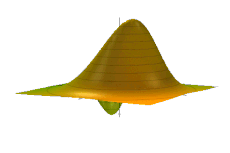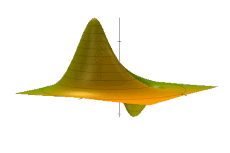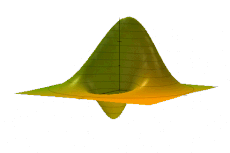
Hi ha diverses maneres diferents de representar la distribució, totes interrelacionades.[ El més destacable és la representació de Wigner, W(x, p), descoberta primer.[4] Altres representacions (en ordre aproximadament descendent de prevalença a la literatura) inclouen les representacions de Glauber–Sudarshan P, Husimi Q, Kirkwood–Rihaczek, Mehta, Rivier i Born–Jordan. Aquestes alternatives són més útils quan l'hammiltonià pren una forma particular, com ara l'ordre normal per a la representació P de Glauber-Sudarshan. Com que la representació de Wigner és la més habitual, aquest article normalment s'hi adhereix, tret que s'especifiqui el contrari.

La distribució d'espai de fase té propietats semblants a la densitat de probabilitat en un espai de fase de 2n dimensions. Per exemple, té un valor real, a diferència de la funció d'ona de valors complexos generalment. Podem entendre la probabilitat d'estar dins d'un interval de posició, per exemple, integrant la funció de Wigner sobre tots els moments i sobre l'interval de posició:

$\operatorname {P} [a\leq X\leq b]=\int _{a}^{b}\int _{-\infty }^{\infty }W(x,p)\,dp\,dx.$

Si Â(x, p) és un operador que representa un observable, es pot assignar a l'espai de fases com A(x, p) mitjançant la transformada de Wigner. Per contra, aquest operador pot ser recuperat per la transformada de Weyl.

$\langle {\hat {A}}\rangle =\int A(x,p)W(x,p)\,dp\,dx.$

Un punt de precaució, però: malgrat la similitud d'aparença, W(x, p) no és una distribució de probabilitat conjunta genuïna, perquè les regions que hi ha sota no representen estats mútuament exclusius, tal com exigeix el tercer axioma de la teoria de la probabilitat. A més, pot, en general, prendre valors negatius fins i tot per als estats purs, amb l'única excepció dels estats coherents (opcionalment comprimits), en violació del primer axioma.

Es pot demostrar que les regions d'aquest valor negatiu són "petites": no poden estendre's a regions compactes més grans que uns pocs ħ, i per tant desapareixen en el límit clàssic. Estan protegits pel principi d'incertesa, que no permet una localització precisa dins de regions de l'espai de fases més petites que ħ, i per tant fa que aquestes "probabilitats negatives" siguin menys paradoxals. Si el costat esquerre de l'equació s'ha d'interpretar com un valor d'expectativa en l'espai de Hilbert respecte a un operador, aleshores en el context de l'òptica quàntica aquesta equació es coneix com el teorema d'equivalència òptica. (Per obtenir més detalls sobre les propietats i la interpretació de la funció Wigner, vegeu el seu article principal).

Un enfocament alternatiu de l'espai de fase a la mecànica quàntica pretén definir una funció d'ona (no només una densitat de quasiprobabilitat) a l'espai de fases, normalment mitjançant la transformada de Segal-Bargmann. Per ser compatible amb el principi d'incertesa, la funció d'ona de l'espai de fase no pot ser una funció arbitrària, o bé es podria localitzar en una regió arbitràriament petita de l'espai de fase. Més aviat, la transformada de Segal-Bargmann és una funció holomòrfica de x+ip. Hi ha una densitat de quasiprobabilitat associada a la funció d'ona espai-fase; és la representació Husimi Q de la funció d'ona de posició.