Homomorfisme (àlgebra)

Diagrama commutatiu d'un homomorfisme de grup

Diagrama de Venn de diferents tipus d'homomorfismes.

En àlgebra, un homomorfisme és un mapa que preserva l'estructura entre dues estructures algebraiques del mateix tipus (com ara dos grups, dos anells o dos espais vectorials). La paraula homomorfisme prové de la llengua grega antiga: ὁμός (homos) que significa "mateix" i μορφή (morphe) que significa "forma". Tanmateix, sembla que la paraula es va introduir a les matemàtiques a causa d'una traducció (mala) de l'alemany ähnlich que significa "similar" a ὁμός que significa "el mateix". El terme "homomorfisme" va aparèixer ja el 1892, quan es va atribuir al matemàtic alemany Felix Klein (1849–1925).

Els homomorfismes d'espais vectorials també s'anomenen mapes lineals, i el seu estudi és objecte d'àlgebra lineal.

El concepte d'homomorfisme s'ha generalitzat, sota el nom de morfisme, a moltes altres estructures que o bé no tenen un conjunt subjacent, o bé no són algebraiques. Aquesta generalització és el punt de partida de la teoria de categories.

Un homomorfisme també pot ser un isomorfisme, un endomorfisme, un automorfisme, etc. (vegeu més avall). Cadascun d'ells es pot definir d'una manera que es pot generalitzar a qualsevol classe de morfismes.

Definició

Un homomorfisme és un mapa entre dues estructures algebraiques del mateix tipus (és a dir, del mateix nom), que conserva les operacions de les estructures. Això vol dir un mapa $f:A\to B$ entre dos conjunts $A$, $B$ equipat amb la mateixa estructura tal que, si $\cdot$ és una operació de l'estructura (suposada aquí, per simplificar, és una operació binària), llavors

$f(x\cdot y)=f(x)\cdot f(y)$

per cada parella $x$, $y$ d'elements de $A$. Això ho diu sovint $f$ conserva el funcionament o és compatible amb el funcionament.

Formalment, un mapa $f:A\to B$ conserva una operació $\mu$ d'aritat $k$, definit en tots dos $A$ i $B$ si

$f(\mu _{A}(a_{1},\ldots ,a_{k}))=\mu _{B}(f(a_{1}),\ldots ,f(a_{k})),$

per a tots els elements $a_{1},...,a_{k}$ en $A$.

Les operacions que s'han de preservar per un homomorfisme inclouen operacions 0-àries, és a dir, les constants. En particular, quan el tipus d'estructura requereix un element d'identitat, l'element d'identitat de la primera estructura s'ha de mapar a l'element d'identitat corresponent de la segona estructura.

Per exemple:

• Un homomorfisme de semigrup és un mapa entre semigrups que conserva l'operació del semigrup.

• Un homomorfisme monoide és un mapa entre monoides que conserva l'operació monoide i mapeja l'element d'identitat del primer monoide amb el del segon monoide (l'element d'identitat és una operació 0-ària).
• Un homomorfisme de grup és un mapa entre grups que preserva l'operació del grup. Això implica que l'homomorfisme de grup mapeja l'element d'identitat del primer grup amb l'element d'identitat del segon grup, i mapeja la inversa d'un element del primer grup a la inversa de la imatge d'aquest element. Així, un homomorfisme de semigrup entre grups és necessàriament un homomorfisme de grup.
• Un homomorfisme d'anells és un mapa entre anells que conserva l'addició d'anells, la multiplicació d'anells i la identitat multiplicativa. Si s'ha de preservar la identitat multiplicativa depèn de la definició d'anell en ús. Si no es conserva la identitat multiplicativa, es té un homomorfisme rng.
• Un mapa lineal és un homomorfisme d'espais vectorials; és a dir, un homomorfisme de grup entre espais vectorials que conserva l'estructura del grup abelià i la multiplicació escalar.
• Un homomorfisme de mòduls, també anomenat mapa lineal entre mòduls, es defineix de manera similar.
• Un homomorfisme d'àlgebra és un mapa que conserva les operacions d'àlgebra.

Una estructura algebraica pot tenir més d'una operació, i es requereix un homomorfisme per preservar cada operació. Així, un mapa que conserva només algunes de les operacions no és un homomorfisme de l'estructura, sinó només un homomorfisme de la subestructura obtingut en considerar només les operacions conservades. Per exemple, un mapa entre monoides que conserva l'operació monoide i no l'element d'identitat, no és un homomorfisme monoide, sinó només un homomorfisme semigrup.

Exemples

Homomorfisme monoide $f$ del monoide

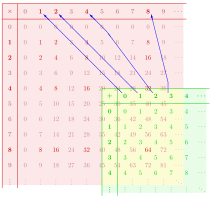
Els nombres reals són un anell, amb suma i multiplicació. El conjunt de totes les matrius 2×2 també és un anell, sota la suma de matrius i la multiplicació de matrius. Si definim una funció entre aquests anells de la següent manera:

$f(r)={\begin{pmatrix}r&0\\0&r\end{pmatrix}}$

on r és un nombre real, aleshores f és un homomorfisme dels anells, ja que f conserva les dues addicions:

$f(r+s)={\begin{pmatrix}r+s&0\\0&r+s\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}+{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)+f(s)$

i multiplicació:

$f(rs)={\begin{pmatrix}rs&0\\0&rs\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)\,f(s).$

Per a un altre exemple, els nombres complexos diferents de zero formen un grup sota l'operació de multiplicació, igual que els nombres reals diferents de zero. (El zero s'ha d'excloure d'ambdós grups ja que no té una inversa multiplicativa, que és necessària per als elements d'un grup)