De la Viquipèdia, l'enciclopèdia lliure
La llei de Morrie és una identitat trigonomètrica singular. El seu nom s'atribueix al físic Richard Feynman , que solia referir-se a aquesta identitat amb aquest nom. Feynman va triar aquest nom perquè la va aprendre durant la seva infantesa a través d'un noi anomenat Morrie Jacob i la va recordar tota la seva vida.[ 1]
cos
(
20
∘
)
⋅
cos
(
40
∘
)
⋅
cos
(
80
∘
)
=
1
8
.
{\displaystyle \cos(20^{\circ })\cdot \cos(40^{\circ })\cdot \cos(80^{\circ })={\frac {1}{8}}.}
És un cas especial de la identitat, més general,
2
n
⋅
∏
k
=
0
n
−
1
cos
(
2
k
α
)
=
sin
(
2
n
α
)
sin
(
α
)
{\displaystyle 2^{n}\cdot \prod _{k=0}^{n-1}\cos(2^{k}\alpha )={\frac {\sin(2^{n}\alpha )}{\sin(\alpha )}}}
amb n = 3 i α = 20° i el fet que
sin
(
160
∘
)
sin
(
20
∘
)
=
sin
(
180
∘
−
20
∘
)
sin
(
20
∘
)
=
1
,
{\displaystyle {\frac {\sin(160^{\circ })}{\sin(20^{\circ })}}={\frac {\sin(180^{\circ }-20^{\circ })}{\sin(20^{\circ })}}=1,}
ja que
sin
(
180
∘
−
x
)
=
sin
(
x
)
.
{\displaystyle \sin(180^{\circ }-x)=\sin(x).}
També existeix una identitat similar amb la funció sinus:
sin
(
20
∘
)
⋅
sin
(
40
∘
)
⋅
sin
(
80
∘
)
=
3
8
.
{\displaystyle \sin(20^{\circ })\cdot \sin(40^{\circ })\cdot \sin(80^{\circ })={\frac {\sqrt {3}}{8}}.}
A més, si es divideix la segona identitat per la primera, s'obté:
tan
(
20
∘
)
⋅
tan
(
40
∘
)
⋅
tan
(
80
∘
)
=
3
=
tan
(
60
∘
)
.
{\displaystyle \tan(20^{\circ })\cdot \tan(40^{\circ })\cdot \tan(80^{\circ })={\sqrt {3}}=\tan(60^{\circ }).}
[ modifica ] Enneàgon regular
A
B
C
D
E
F
G
H
I
{\displaystyle ABCDEFGHI}
circumferència circumscrita
O
{\displaystyle O}
40
∘
=
360
∘
9
70
∘
=
180
∘
−
40
∘
2
α
=
180
∘
−
90
∘
−
70
∘
=
20
∘
β
=
180
∘
−
90
∘
−
(
70
∘
−
α
)
=
40
∘
γ
=
140
∘
−
β
−
α
=
80
∘
{\displaystyle {\begin{aligned}40^{\circ }&={\frac {360^{\circ }}{9}}\\70^{\circ }&={\frac {180^{\circ }-40^{\circ }}{2}}\\\alpha &=180^{\circ }-90^{\circ }-70^{\circ }=20^{\circ }\\\beta &=180^{\circ }-90^{\circ }-(70^{\circ }-\alpha )=40^{\circ }\\\gamma &=140^{\circ }-\beta -\alpha =80^{\circ }\end{aligned}}}
Consideri's l'enneàgon regular
A
B
C
D
E
F
G
H
I
{\displaystyle ABCDEFGHI}
1
{\displaystyle 1}
M
{\displaystyle M}
A
B
{\displaystyle AB}
L
{\displaystyle L}
B
F
{\displaystyle BF}
J
{\displaystyle J}
B
D
{\displaystyle BD}
140
∘
{\displaystyle 140^{\circ }}
γ
=
∠
F
B
M
=
80
∘
{\displaystyle \gamma =\angle FBM=80^{\circ }}
β
=
∠
D
B
F
=
40
∘
{\displaystyle \beta =\angle DBF=40^{\circ }}
α
=
∠
C
B
D
=
20
∘
{\displaystyle \alpha =\angle CBD=20^{\circ }}
definició del cosinus en els triangles rectangles
△
B
F
M
{\displaystyle \triangle BFM}
△
B
D
L
{\displaystyle \triangle BDL}
△
B
C
J
{\displaystyle \triangle BCJ}
[ 2]
1
=
|
A
B
|
=
2
⋅
|
M
B
|
=
2
⋅
|
B
F
|
⋅
cos
(
γ
)
=
2
2
|
B
L
|
cos
(
γ
)
=
2
2
⋅
|
B
D
|
⋅
cos
(
γ
)
⋅
cos
(
β
)
=
2
3
⋅
|
B
J
|
⋅
cos
(
γ
)
⋅
cos
(
β
)
=
2
3
⋅
|
B
C
|
⋅
cos
(
γ
)
⋅
cos
(
β
)
⋅
cos
(
α
)
=
2
3
⋅
1
⋅
cos
(
γ
)
⋅
cos
(
β
)
⋅
cos
(
α
)
=
8
⋅
cos
(
80
∘
)
⋅
cos
(
40
∘
)
⋅
cos
(
20
∘
)
{\displaystyle {\begin{aligned}1&=|AB|\\&=2\cdot |MB|\\&=2\cdot |BF|\cdot \cos(\gamma )\\&=2^{2}|BL|\cos(\gamma )\\&=2^{2}\cdot |BD|\cdot \cos(\gamma )\cdot \cos(\beta )\\&=2^{3}\cdot |BJ|\cdot \cos(\gamma )\cdot \cos(\beta )\\&=2^{3}\cdot |BC|\cdot \cos(\gamma )\cdot \cos(\beta )\cdot \cos(\alpha )\\&=2^{3}\cdot 1\cdot \cos(\gamma )\cdot \cos(\beta )\cdot \cos(\alpha )\\&=8\cdot \cos(80^{\circ })\cdot \cos(40^{\circ })\cdot \cos(20^{\circ })\end{aligned}}}
[ modifica ] Recordeu la fórmula de l'angle doble per a la funció sinus
sin
(
2
α
)
=
2
sin
(
α
)
cos
(
α
)
.
{\displaystyle \sin(2\alpha )=2\sin(\alpha )\cos(\alpha ).}
Si s'aïlla
cos
(
α
)
{\displaystyle \cos(\alpha )}
cos
(
α
)
=
sin
(
2
α
)
2
sin
(
α
)
.
{\displaystyle \cos(\alpha )={\frac {\sin(2\alpha )}{2\sin(\alpha )}}.}
Segueix:
cos
(
2
α
)
=
sin
(
4
α
)
2
sin
(
2
α
)
cos
(
4
α
)
=
sin
(
8
α
)
2
sin
(
4
α
)
⋮
cos
(
2
n
−
1
α
)
=
sin
(
2
n
α
)
2
sin
(
2
n
−
1
α
)
.
{\displaystyle {\begin{aligned}\cos(2\alpha )&={\frac {\sin(4\alpha )}{2\sin(2\alpha )}}\\[6pt]\cos(4\alpha )&={\frac {\sin(8\alpha )}{2\sin(4\alpha )}}\\&\,\,\,\vdots \\\cos \left(2^{n-1}\alpha \right)&={\frac {\sin \left(2^{n}\alpha \right)}{2\sin \left(2^{n-1}\alpha \right)}}.\end{aligned}}}
Si es multipliquen totes aquestes expressions juntes s'obté:
cos
(
α
)
cos
(
2
α
)
cos
(
4
α
)
⋯
cos
(
2
n
−
1
α
)
=
sin
(
2
α
)
2
sin
(
α
)
⋅
sin
(
4
α
)
2
sin
(
2
α
)
⋅
sin
(
8
α
)
2
sin
(
4
α
)
⋯
sin
(
2
n
α
)
2
sin
(
2
n
−
1
α
)
.
{\displaystyle \cos(\alpha )\cos(2\alpha )\cos(4\alpha )\cdots \cos \left(2^{n-1}\alpha \right)={\frac {\sin(2\alpha )}{2\sin(\alpha )}}\cdot {\frac {\sin(4\alpha )}{2\sin(2\alpha )}}\cdot {\frac {\sin(8\alpha )}{2\sin(4\alpha )}}\cdots {\frac {\sin \left(2^{n}\alpha \right)}{2\sin \left(2^{n-1}\alpha \right)}}.}
Els numeradors i denominadors del mig s'anul·len deixant només el primer denominador, una potència de 2 i el numerador final. Noti's que hi ha n termes en tots dos costats de l'expressió. És a dir,
∏
k
=
0
n
−
1
cos
(
2
k
α
)
=
sin
(
2
n
α
)
2
n
sin
(
α
)
,
{\displaystyle \prod _{k=0}^{n-1}\cos \left(2^{k}\alpha \right)={\frac {\sin \left(2^{n}\alpha \right)}{2^{n}\sin(\alpha )}},}
que és equivalent a la generalització de la llei de Morrie.
↑ W. A. Beyer, J. D. Louck, and D. Zeilberger , A Generalization of a Curiosity that Feynman Remembered All His Life , Math. Mag. 69, 43–44, 1996. (JSTOR )
↑ Samuel G. Moreno, Esther M. García-Caballero: "'A Geometric Proof of Morrie's Law". In: American Mathematical Monthly , vol. 122, no. 2 (February 2015), p. 168 (JSTOR )
Glen Van Brummelen: Trigonometry: A Very Short Introduction . Oxford University Press, 2020, ISBN 9780192545466 , pp. 79-83
Ernest C. Anderson: Morrie's Law and Experimental Mathematics . In: Journal of recreational mathematics , 1998 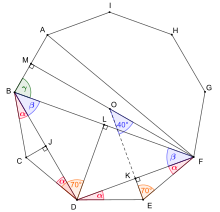




























![{\displaystyle {\begin{aligned}\cos(2\alpha )&={\frac {\sin(4\alpha )}{2\sin(2\alpha )}}\\[6pt]\cos(4\alpha )&={\frac {\sin(8\alpha )}{2\sin(4\alpha )}}\\&\,\,\,\vdots \\\cos \left(2^{n-1}\alpha \right)&={\frac {\sin \left(2^{n}\alpha \right)}{2\sin \left(2^{n-1}\alpha \right)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60bd81aaf5f880106a8afbd298449d2818660709)

