Llista d'identitats trigonomètriques

En matemàtiques, les identitats trigonomètriques són igualtats que impliquen funcions trigonomètriques i que són veritat per a qualsevol valor de les variables. Aquestes identitats són útils quan cal simplificar expressions en què intervenen funcions trigonomètriques. Una aplicació important és la integració de funcions no trigonomètriques: un truc habitual és començar per fer servir la integració per canvi de variable amb una funció trigonomètrica i llavors simplificar la integral resultant amb una identitat trigonomètrica.

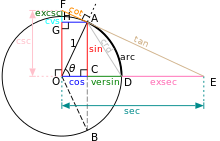
Totes les funcions trigonomètriques d'un angle θ es poden construir geomètricament a partir de la circumferència goniomètrica.

La circumferència goniomètrica

En aquest article es llisten aquestes identitats, per a la seva demostració vegeu demostració de les identitats trigonomètriques

Notació

Per tal d'evitar confusió causada per l'ambigüitat de sin⁻¹(x), les inverses respecte del producte i les inverses de les funcions trigonomètriques sovint s'escriuen tal com es presenten a la següent taula. En representar la funció cosecant, de vegades es fa servir la forma llarga 'cosec' en comptes de 'csc'.

Funció		funció inversa		Inversa multiplicativa		Funció inversa de la inversa
sinus	sin	arcsinus	arcsin	cosecant	csc	arccosecant	arccsc
cosinus	cos	arccosinus	arccos	secant	sec	arcsecant	arcsec
tangent	tan	arctangent	arctan	cotangent	cot	arccotangent	arccot

Diferents sistemes de mesura dels angles poden ser més apropiats per a diferents situacions. Aquesta taula presenta algunes les equivalències entre alguns angles pels tres sistemes més comuns. Els radiants són la unitat de mesura més adequada per aplicacions matemàtiques i per a la majoria d'aplicacions en física. És el sistema que es fa servir si les funcions trigonomètriques es defineixen emprant exponencials. En algunes aplicacions de física i moltes de mecànica, té l'inconvenient de què un nombre sencer de voltes o una fracció racional d'una volta correspon a un angle expressat per un nombre irracional, per això es continuen fent servir les voltes i els sistemes dels graus sexagesimals o centesimals. Totes les mesures angulars són adimensionals.

Graus	30	45	60	90	120	180	270	360
radiants	$\pi /6$	$\pi /4$	$\pi /3$	$\pi /2$	$2\pi /3$	$\pi$	$3\pi /2$	$2\pi$
Graus centesimals	33 ⅓	50	66 ⅔	100	133 ⅓	200	300	400
Voltes	1/12	1/8	2/12	1/4	1/3	1/2	3/4	1

Relacions bàsiques

Identitat trigonomètrica pitagòrica	$\sin ^{2}\theta +\cos ^{2}\theta =1\,$
Identitat del quocient	$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

A partir d'aquestes dues identitats, es pot obtenir la següent taula. Fixeu-vos, però, que aquestes equacions de conversió no poden donar el signe correcte sign (+ o −). Per exemple, si sin θ = 1/2, la taula indica que $\scriptstyle \cos \theta \,=\,{\sqrt {1-\sin ^{2}\theta }}={\sqrt {3}}/2$, però pot ser que $\scriptstyle \cos \theta \,=\,-{\sqrt {3}}/2$. Cal més informació respecte a quin quadrant pertany θ per a determinar el signe.

Cada una de les funcions trigonomètriques expressada en funció de cada una de les altres cinc.

Funció	sin	cos	tan	csc	sec	cot
$\sin \theta =$	$\sin \theta \$	${\sqrt {1-\cos ^{2}\theta }}$	${\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {1}{\csc \theta }}$	${\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}$	${\frac {1}{\sqrt {1+\cot ^{2}\theta }}}$
$\cos \theta =$	${\sqrt {1-\sin ^{2}\theta }}$	$\cos \theta \$	${\frac {1}{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}$	${\frac {1}{\sec \theta }}$	${\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}$
$\tan \theta =$	${\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}$	${\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}$	$\tan \theta \$	${\frac {1}{\sqrt {\csc ^{2}\theta -1}}}$	${\sqrt {\sec ^{2}\theta -1}}$	${\frac {1}{\cot \theta }}$
$\csc \theta =$	${1 \over \sin \theta }$	${1 \over {\sqrt {1-\cos ^{2}\theta }}}$	${{\sqrt {1+\tan ^{2}\theta }} \over \tan \theta }$	$\csc \theta \$	${\sec \theta \over {\sqrt {\sec ^{2}\theta -1}}}$	${\sqrt {1+\cot ^{2}\theta }}$
$\sec \theta =$	${1 \over {\sqrt {1-\sin ^{2}\theta }}}$	${1 \over \cos \theta }$	${\sqrt {1+\tan ^{2}\theta }}$	${\csc \theta \over {\sqrt {\csc ^{2}\theta -1}}}$	$\sec \theta \$	${{\sqrt {1+\cot ^{2}\theta }} \over \cot \theta }$
$\cot \theta =$	${{\sqrt {1-\sin ^{2}\theta }} \over \sin \theta }$	${\cos \theta \over {\sqrt {1-\cos ^{2}\theta }}}$	${1 \over \tan \theta }$	${\sqrt {\csc ^{2}\theta -1}}$	${1 \over {\sqrt {\sec ^{2}\theta -1}}}$	$\cot \theta \$

Funcions arcaiques

Encara que avui en dia es fan servir rarament, el versinus, el coversinus, el semiversinus, i l'exsecant es poden definir tal com es presenta en la següent taula i s'han fet servir en navegació, per exemple la fórmula del Haversine es feia servir per a calcular la distància entre dos punts situats sobre una esfera.

Nom	Valor
${\textrm {versin}}\,\theta$	$1-\cos \theta \,$
${\textrm {coversin}}\,\theta$	$1-\sin \theta \,$
${\textrm {semiversin}}\,\theta$	${\tfrac {1}{2}}{\textrm {versin}}\theta \,$
${\textrm {exsec}}\,\theta \,$	$\sec \theta -1\,$

Simetries, desplaçaments i periodicitat

Examinant la circumferència goniomètrica es poden establir les següents propietats de les funcions trigonomètriques.

Simetria

Quan les funcions trigonomètriques es reflecteixen respecte als eixos que formen certs angles $\theta$, el resultat és sovint una altra de les funcions trigonomètriques. Això porta a les següents identitats:

Reflexió respecte l'eix $\theta =0$	Reflexió respecte l'eix $\theta =\pi /2$	Reflexió respecte l'eix $\theta =\pi$
${\begin{aligned}\sin(0-\theta )&=-\sin \theta \\\cos(0-\theta )&=+\cos \theta \\\tan(0-\theta )&=-\tan \theta \\\csc(0-\theta )&=-\csc \theta \\\sec(0-\theta )&=+\sec \theta \\\cot(0-\theta )&=-\cot \theta \end{aligned}}$	${\begin{aligned}\sin({\tfrac {\pi }{2}}-\theta )&=+\cos \theta \\\cos({\tfrac {\pi }{2}}-\theta )&=+\sin \theta \\\tan({\tfrac {\pi }{2}}-\theta )&=+\cot \theta \\\csc({\tfrac {\pi }{2}}-\theta )&=+\sec \theta \\\sec({\tfrac {\pi }{2}}-\theta )&=+\csc \theta \\\cot({\tfrac {\pi }{2}}-\theta )&=+\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\pi -\theta )&=+\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \\\csc(\pi -\theta )&=+\csc \theta \\\sec(\pi -\theta )&=-\sec \theta \\\cot(\pi -\theta )&=-\cot \theta \\\end{aligned}}$

Desplaçaments i periodicitat

Desplaçant l'argument de la funció certs angles, sovint es poden trobar altres funcions trigonomètriques que expressen el resultat de forma més senzilla. A la següent taula es presenten alguns exemples a base de desplaçar els arguments angles de π/2, π i 2π radiants. Com que els períodes d'aquestes funcions són o bé π o bé 2π, hi ha casos on les noves funcions són exactament les mateixes que les antigues abans del desplaçament.

Desplaçament de π/2	Desplaçament de π Període de la tan i la cot	Desplaçament de 2π Període del sin, del cos, la csc i la sec
${\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\csc(\theta +{\tfrac {\pi }{2}})&=+\sec \theta \\\sec(\theta +{\tfrac {\pi }{2}})&=-\csc \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\csc(\theta +\pi )&=-\csc \theta \\\sec(\theta +\pi )&=-\sec \theta \\\cot(\theta +\pi )&=+\cot \theta \\\end{aligned}}$	${\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\csc(\theta +2\pi )&=+\csc \theta \\\sec(\theta +2\pi )&=+\sec \theta \\\cot(\theta +2\pi )&=+\cot \theta \end{aligned}}$

Identitats de la suma i diferència d'angles

Sinus	$\sin(\theta \pm \varphi )=\sin \theta \cos \varphi \pm \cos \theta \sin \varphi \,$	Nota: A partir del signe mes-menys. ${\begin{aligned}x\pm y=a\pm b&\Rightarrow \ x+y=a+b\\&{\mbox{i}}\ x-y=a-b\end{aligned}}$ ${\begin{aligned}x\pm y=a\mp b&\Rightarrow \ x+y=a-b\\&{\mbox{i}}\ x-y=a+b\end{aligned}}$
Cosinus	$\cos(\theta \pm \varphi )=\cos \theta \cos \varphi \mp \sin \theta \sin \varphi \,$
Tangent	$\tan(\theta \pm \varphi )={\frac {\tan \theta \pm \tan \varphi }{1\mp \tan \theta \tan \varphi }}$

Sinus i cosinus de la suma d'infinits termes

$\sin \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {odd} \ k\geq 1}(-1)^{(k-1)/2}\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

$\cos \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {even} \ k\geq 0}~(-1)^{k/2}~~\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

En aquestes dues identitats apareix una asimetria que no surt en els cas de la suma d'una quantitat finita de termes: en cada producte, només hi ha una quantitat finita de factors sinus i una quantitat cofinita de factors cosinus.

Si només hi ha una quantitat finita de termes θ_i diferents de zero, llavors només una quantitat finita dels termes de la dreta seran diferents de zero perquè els factors sinus s'anul·laran, i a cada terme, tots els factors cosinus tret d'una quantitat finita valdran 1..

Tangents de sumes d'una quantitat finita de termes

Sia x_i = tan(θ_i ), per i = 1, ..., n. Sia e_k el polinomi simètric elemental en les variables x_i, i = 1, ..., n, k = 0, ..., n. Llavors

$\tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},$

El nombre de termes depèn de n.

Per exemple,

${\begin{aligned}\tan(\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}$

I així. El cas general es pot demostrar per inducció.

Fórmules de l'angle múltiple

Tn és l'n-èsim polinomi de Txebixov	$\cos n\theta =T_{n}(\cos \theta )\,$
Sn és l'n-èsim polinomi d'obertura	$\sin ^{2}n\theta =S_{n}(\sin ^{2}\theta )\,$
Fórmula de De Moivre, $i$ és la unitat imaginària	$\cos n\theta +i\sin n\theta =(\cos(\theta )+i\sin(\theta ))^{n}\,$

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}.$

(Aquesta funció de x és el nucli de Dirichlet.)

Fórmules de l'angle doble, triple i meitat

Aquestes expressions es poden demostrar fent servir ja sigui les identitats de la suma i de la diferència o bé amb les identitats de l'angle múltiple.

Fórmules de l'angle doble
${\begin{aligned}\sin 2\theta &=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}$	${\begin{aligned}\cos 2\theta &=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}$	$\tan 2\theta ={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\,$	$\cot 2\theta ={\frac {\cot \theta -\tan \theta }{2}}\,$
Fórmules de l'angle triple
$\sin 3\theta =3\sin \theta -4\sin ^{3}\theta \,$	$\cos 3\theta =4\cos ^{3}\theta -3\cos \theta \,$	$\tan 3\theta ={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}$
Fórmules de l'angle meitat
$\sin {\tfrac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}$	$\cos {\tfrac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}}$	${\begin{aligned}\tan {\tfrac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\end{aligned}}$	$\cot {\tfrac {\theta }{2}}=\csc \theta +\cot \theta$

Vegeu també fórmula de la tangent de l'angle meitat.

En general:

$\sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left({\frac {1}{2}}(n-k)\pi \right)$

$\cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left({\frac {1}{2}}(n-k)\pi \right)$

$\tan n\theta \,$ es pot escriure emprant la relació recurrent:

$\tan n\theta ={\frac {\tan \left(\left(n-1\right)\theta \right)+\tan \theta }{1-\tan \left(\left(n-1\right)\theta \right)\tan \theta }}$

Producte infinit d'Euler

$\cos \left({\theta \over 2}\right)\cdot \cos \left({\theta \over 4}\right)\cdot \cos \left({\theta \over 8}\right)\cdots =\prod _{n=1}^{\infty }\cos \left({\theta \over 2^{n}}\right)={\sin(\theta ) \over \theta }.$

Fórmules de reducció de potències

S'obtenen resolent les versions segona i tercera de la fórmula del cosinus de l'angle doble.

Sinus	$\sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}$	$\sin ^{3}\theta ={\frac {3\sin \theta -\sin 3\theta }{4}}$	$\sin ^{4}\theta ={\frac {3-4\cos 2\theta +\cos 4\theta }{8}}$	$\sin ^{5}\theta ={\frac {10\sin \theta -5\sin 3\theta +\sin 5\theta }{16}}$
Cosinus	$\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}$	$\cos ^{3}\theta ={\frac {3\cos \theta +\cos 3\theta }{4}}$	$\cos ^{4}\theta ={\frac {3+4\cos 2\theta +\cos 4\theta }{8}}$	$\cos ^{5}\theta ={\frac {10\cos \theta +5\cos 3\theta +\cos 5\theta }{16}}$
Altre	$\sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos 4\theta }{8}}$	$\sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin 2\theta -\sin 6\theta }{32}}$	$\sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos 4\theta +\cos 8\theta }{128}}$	$\sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin 2\theta -5\sin 6\theta +\sin 10\theta }{512}}$

Fórmules de Simpson

Transformació de productes en sumes $\cos \theta \cos \varphi ={\cos(\theta -\varphi )+\cos(\theta +\varphi ) \over 2}$ $\sin \theta \sin \varphi ={\cos(\theta -\varphi )-\cos(\theta +\varphi ) \over 2}$ $\sin \theta \cos \varphi ={\sin(\theta +\varphi )+\sin(\theta -\varphi ) \over 2}$

Transformació de sumes en productes $\sin \theta +\sin \varphi =2\sin \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)$ $\cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)$ $\cos \theta -\cos \varphi =-2\sin \left({\theta +\varphi \over 2}\right)\sin \left({\theta -\varphi \over 2}\right)$ $\sin \theta -\sin \varphi =2\cos \left({\theta +\varphi \over 2}\right)\sin \left({\theta -\varphi \over 2}\right)\;$

Altres identitats relacionades

Si x, y, i z són els tres angles d'un triangle qualsevol, o en altres paraules

${\mbox{Si }}x+y+z=\pi ={\mbox{mitja volta,}}\,$

${\mbox{llavors }}\tan(x)+\tan(y)+\tan(z)=\tan(x)\tan(y)\tan(z).\,$

(Si qualsevol dels angles x, y, z és un angle recte, ha d'adoptar els dos cantons de l'∞. És a di, ni +∞ ni −∞; pels objectius actuals, té sentit afegir només un punt a l'infinit de la línia real, és a dir el límit de la tan(θ) tant a mesura que la tan(θ) creix amb valors positius com quant disminueix amb valors negatius. Això és una compactació d'Alexandroff de la recta real.)

${\mbox{Si }}x+y+z=\pi ={\mbox{mitja volta,}}\,$

${\mbox{llavors }}\sin(2x)+\sin(2y)+\sin(2z)=4\sin(x)\sin(y)\sin(z).\,$

Teorema de Ptolemeu

${\mbox{Si }}w+x+y+z=\pi ={\mbox{mitja volta,}}\,$

${\begin{aligned}{\mbox{llavors }}&\sin(w+x)\sin(x+y)\\&{}=\sin(x+y)\sin(y+z)\\&{}=\sin(y+z)\sin(z+w)\\&{}=\sin(z+w)\sin(w+x)=\sin(w)\sin(y)+\sin(x)\sin(z).\end{aligned}}$

(Les tres primeres igualtats són trivials; la quarta és la substància d'aquesta identitat.) Essencialment és el teorema de Ptolemeu adaptat al llenguatge de la trigonometria.

Combinacions lineals

Per algunes aplicacions és important saber que qualsevol combinació lineal d'ones sinusoidal del mateix període però de diferent fase és també una ona sinusoidal amb el pateix període però amb una altra fase diferent. En el cas de una combinació lineal d'ones sinusoidals i cosinusoidals, es té

$a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\,$

on

$\varphi =\arcsin \left({\frac {b}{\sqrt {a^{2}+b^{2}}}}\right)$

De forma més general, per a qualsevol desplaçament de fase, es té

$a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\,$

on

$c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},$

i

$\beta ={\rm {arctan}}\left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right).$

Altres sumes de funcions trigonomètriques

Sumes de sinus i de cosinus am arguments en progressió aritmètica:

$\sin {\varphi }+\sin {(\varphi +\alpha )}+\sin {(\varphi +2\alpha )}+\cdots +\sin {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \sin {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.$

$\cos {\varphi }+\cos {(\varphi +\alpha )}+\cos {(\varphi +2\alpha )}+\cdots +\cos {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \cos {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.$

Per a qualsevol a i b:

$a\cos(x)+b\sin(x)={\sqrt {a^{2}+b^{2}}}\cos(x-\arctan(b,a))\;$

on arctan(y, x) és la generalització de l'arctan(y/x) que cobreix el recorregut circular complet.

$\tan(x)+\sec(x)=\tan \left({x \over 2}+{\pi \over 4}\right).$

És convenient conèixer la identitat de més amunt, en estudiar la funció Gudermanniana.

Si x, y, i z són els tres angles d'un triangle, és a dir, si x + y + z = π, llavors

$\cot(x)\cot(y)+\cot(y)\cot(z)+\cot(z)\cot(x)=1.\,$

Inverses de les funcions trigonomètriques

$\arcsin(x)+\arccos(x)=\pi /2\;$

$\arctan(x)+\operatorname {arccot}(x)=\pi /2.\;$

$\arctan(x)+\arctan(1/x)=\left\{{\begin{matrix}\pi /2,&{\mbox{if }}x>0\\-\pi /2,&{\mbox{if }}x<0\end{matrix}}\right.$

Composicions de funcions trigonomètriques amb inverses de funcions trigonomètriques

$\sin[\arccos(x)]={\sqrt {1-x^{2}}}\,$ $\sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}$ $\cos[\arctan(x)]={\frac {1}{\sqrt {1+x^{2}}}}$ $\cos[\arcsin(x)]={\sqrt {1-x^{2}}}\,$

$\tan[\arcsin(x)]={\frac {x}{\sqrt {1-x^{2}}}}$ $\tan[\arccos(x)]={\frac {\sqrt {1-x^{2}}}{x}}$ $\cot[\arcsin(x)]={\frac {\sqrt {1-x^{2}}}{x}}$ $\cot[\arccos(x)]={\frac {x}{\sqrt {1-x^{2}}}}$

Relació amb la funció exponencial inversa

$e^{ix}=\cos(x)+i\sin(x)\,$ (Fórmula d'Euler),

$e^{-ix}=\cos(-x)+i\sin(-x)=\cos(x)-i\sin(x)\,$

$e^{i\pi }=-1\,$

$\cos(x)={\frac {e^{ix}+e^{-ix}}{2}}\;$

$\sin(x)={\frac {e^{ix}-e^{-ix}}{2i}}\;$

on i² = −1.

Cis

De vegades es troba aquesta notació

$\operatorname {cis} (x)=\cos(x)+i\sin(x),\,$

És a dir "cis" és una forma d'abreujar "cos + i sin".

Tot i que a primer cop d'ull aquesta notació és redundant, perquè és equivalent a e^ix, és seu ús es basa en diversos avantatges.

Conveniència

Aquesta notació era més habitual quant es feien servir màquines d'escriure per a escriure expressions matemàtiques. Els superíndexs estan desplaçats verticalment i són més petits que 'cis' o 'exp'; per tant, poden ser problemàtics fins i tot en l'escriptura manual. Per exemple e ^ix² versus cis(x²) versus exp(ix²). Per a molts lectors, cis(x²) és el més clar, el més fàcil de llegir dels tres.

La notació cis de vegades es fa servir per a emfatitzar una forma de veure i de tractar amb un problema sobre una altra forma. Les matemàtiques de la trigonometria i dels exponencials estan relacionades però no són exactament el mateix; la notació exponencial emfatitza el conjunt, mentre que les notacions cis i cos + i sin emfatitzen les parts. Això pot ser útil des del punt de vista retòric als matemàtics i als enginyers quan quant discuteixen aquesta funció, i més endavant serveix com un mnemotècnic (per recordar cos + i sin).

La notació cis és convenient per als estudiants de matemàtiques que tenen uns coneixements de trigonometria i de nombres complexos suficient per a permetre aquesta notació, però que encara no entenen els conceptes necessaris per a admetre la notació e ^ix. A mesura que els estudiants aprenen conceptes que construeixen sobre els coneixements previs, és important no forçar-los a emprar nivells de matemàtiques per als quals encara no estan preparats: la demostració de què cis(x) = e^ix requereix càlcul, i l'estudiant pot ser que no hagi estudiat prèviament a haver torbat l'expressió cos(x) + i sin(x).

Pedagogia

En alguns contextos, la notació cis pot servir per a l'objectiu pedagògic d'emfatitzar que encara no s'ha demostrat que és una funció exponencial. En estudiar la trigonometria sense els nombres complexos, es poden demostrar les dues identitats

$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)=c_{1}c_{2}-s_{1}s_{2},\,$

$\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)=s_{1}c_{2}+c_{1}s_{2}.\,$

De forma similar en estudiar la multiplicació de nombres complexos (sense implicacions de la trigonometria), es pot observar que les parts real i imaginària del producte de c₁ + is₁ i c₂ + is₂ són respectivament

$c_{1}c_{2}-s_{1}s_{2},\,$

$s_{1}c_{2}+c_{1}s_{2}.\,$

Així es veu que sorgeix el mateix patró en dos contexts dispars:

• trigonometria sense nombres complexos, i
• nombres complexos sense trigonometria.

Aquesta coincidència pot servir com a motivació per a conjuntar els dos contextos i descobrir la identitat trigonomètrica

$\operatorname {cis} (x+y)=\operatorname {cis} (x)\operatorname {cis} (y),\,$

I observar que aquesta identitat per a la funció cis d'una suma és mes senzilla que les identitats del sinus i el cosinus de la suma d'angles. Un cop s'ha demostrat aquesta identitat, es pot reptar als estudiants a recordar quina mena de funcions que els són familiars satisfan la mateixa equació funcional

$f(x+y)=f(x)f(y).\,$

La resposta és les funcions exponencials. Això suggereix que cis pot ser una funció exponencial

$\operatorname {cis} (x)=b^{x}.\,$

Llavors la qüestió és: quina és la base b? La definició de cis i el comportament local del sinus i del cosinus a prop de zero suggereix que

$\operatorname {cis} (0+dx)=\operatorname {cis} (0)+i\,dx,$

(on dx és un increment infinitesimal de x). Així la velocitat de canvi a 0 és i, per tant la base ha de ser eⁱ. Per tant, si aquesta és una funció exponencial, llavors ha de ser

$\operatorname {cis} (x)=e^{ix}.\,$

Fórmula del producte infinit

Per aplicacions a funcions especials, els següents productes infinits de funcions trigonomètriques són útils:

$\sin x=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$ $\sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$ ${\frac {\sin x}{x}}=\prod _{n=1}^{\infty }\cos \left({\frac {x}{2^{n}}}\right)$

$\cos x=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$ $\cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$

La funció Gudermanniana

La funció Gudermanniana relaciona les funcions trigonomètriques circulars i les funcions trigonomètriques hiperbòliques sense recórrer als nombres complexos; vegeu l'article per a més detalls.

Identitats sense variables

La llei de Morrie

$\cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}}$

És un cas especial d'una identitat que conté una variable:

$\prod _{j=0}^{k-1}\cos(2^{j}x)={\frac {\sin(2^{k}x)}{2^{k}\sin(x)}}.$

Una identitat amb un aspecte semblant és

$\cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{8}},$

I en addició

$\sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\sqrt {3}}/8.$

La següent potser no és tan clarament generalitzada a una identitat que contingui variables:

$\cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.$

Les mesures en graus deixen de ser més oportunes que en radiants quant es considera la següent identitat amb 21 als denominadors:

$\cos \left({\frac {2\pi }{21}}\right)\,+\,\cos \left(2\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(4\cdot {\frac {2\pi }{21}}\right)$

$\,+\,\cos \left(5\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(8\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.$

Els factors 1, 2, 4, 5, 8, 10 poden comença a aclarir el patró: són els enters més petits de 21/2 que són primers entre si amb (o no tenen cap factor primer en comú amb) 21. Els últims exemples són corol·laris d'un fet basic referent als polinomis ciclotomics: els cosinus són les parts reals dels zeros d'aquests polinomis; la suma dels zeros és la funció de Möbius avaluada a (per a l'últim dels casos de més amunt) 21; només la meitat dels zeros són presents més amunt. Les dues identitats precedents a l'última sorgeixen de la mateixa forma substituint 21 per 10 i 15 respectivament.

Una forma eficient de calcular el nombre pi es basa en la següent identitat sense variables, deguda a John Machin:

${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$

o, alternativament, emprant la fórmula d'Euler:

${\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}.$

${\begin{matrix}\sin 0&=&\sin 0^{\circ }&=&0&=&\cos 90^{\circ }&=&\cos \left({\frac {\pi }{2}}\right)\\\\\sin \left({\frac {\pi }{6}}\right)&=&\sin 30^{\circ }&=&1/2&=&\cos 60^{\circ }&=&\cos \left({\frac {\pi }{3}}\right)\\\\\sin \left({\frac {\pi }{4}}\right)&=&\sin 45^{\circ }&=&{\sqrt {2}}/2&=&\cos 45^{\circ }&=&\cos \left({\frac {\pi }{4}}\right)\\\\\sin \left({\frac {\pi }{3}}\right)&=&\sin 60^{\circ }&=&{\sqrt {3}}/2&=&\cos 30^{\circ }&=&\cos \left({\frac {\pi }{6}}\right)\\\\\sin \left({\frac {\pi }{2}}\right)&=&\sin 90^{\circ }&=&1&=&\cos 0^{\circ }&=&\cos 0\end{matrix}}$

$\sin {\frac {\pi }{7}}={\frac {\sqrt {7}}{6}}-{\frac {\sqrt {7}}{189}}\sum _{j=0}^{\infty }{\frac {(3j+1)!}{189^{j}j!\,(2j+2)!}}\!$

$\sin {\frac {\pi }{18}}={\frac {1}{6}}\sum _{j=0}^{\infty }{\frac {(3j)!}{27^{j}j!\,(2j+1)!}}\!$

Amb la secció àuria φ:

$\cos \left({\frac {\pi }{5}}\right)=\cos 36^{\circ }={{\sqrt {5}}+1 \over 4}=\varphi /2$

$\sin \left({\frac {\pi }{10}}\right)=\sin 18^{\circ }={{\sqrt {5}}-1 \over 4}={\varphi -1 \over 2}={1 \over 2\varphi }$

Vegeu també constants trigonomètriques exactes.

Càlcul infinitesimal

En càlcul les relacions que s'estableixen tot seguit requereixen que els angles s'expressin en radiants. Si les funcions trigonomètriques es defineixen sobre la base del triangle rectangle, les seves derivades es poden trobar verificant dos límits. El primer és:

$\lim _{x\rightarrow 0}{\frac {\sin(x)}{x}}=1,$

El segon és:

$\lim _{x\rightarrow 0}{\frac {1-\cos(x)}{x}}=0,$

La resta de les funcions trigonomètriques es poden derivar emprant les identitats anteriors i les regles de derivació:

${\begin{matrix}{d \over dx}\sin x=&\cos x,&{d \over dx}\arcsin x=&{1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x=&-\sin x,&{d \over dx}\arccos x=&{-1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\tan x=&\sec ^{2}x,&{d \over dx}\arctan x=&{1 \over 1+x^{2}}\\\\{d \over dx}\cot x=&-\csc ^{2}x,&{d \over dx}\operatorname {arccot} x=&{-1 \over 1+x^{2}}\\\\{d \over dx}\sec x=&\tan x\sec x,&{d \over dx}\operatorname {arcsec} x=&{1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x=&-\csc x\cot x,&{d \over dx}\operatorname {arccsc} x=&{-1 \over |x|{\sqrt {x^{2}-1}}}\end{matrix}}$

Les identitats per a la integral es poden trobar a "Llista d'integrals de funcions trigonomètriques".

Implicacions

El fet que de la derivada de les funcions trigonomètriques (sinus i cosinus) en resulti una combinació lineal de les mateixes dues funcions és d'importància fonamental en molts camps de la matemàtica, incloent les equacions diferencials i les transformades de Fourier.

Definicions exponencials

Funció	Funció inversa
$\sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,$	$\arcsin x=-i\ln \left(ix+{\sqrt {1-x^{2}}}\right)\,$
$\cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\,$	$\arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)\,$
$\tan \theta ={\frac {e^{i\theta }-e^{-i\theta }}{i(e^{i\theta }+e^{-i\theta })}}\,$	$\arctan x={\frac {i\ln \left({\frac {i+x}{i-x}}\right)}{2}}\,$
$\csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}\,$	$\operatorname {arccsc} x=-i\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,$
$\sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}\,$	$\operatorname {arcsec} x=-i\ln \left({\tfrac {1}{x}}+{\sqrt {1-{\tfrac {i}{x^{2}}}}}\right)\,$
$\cot \theta ={\frac {i(e^{i\theta }+e^{-i\theta })}{e^{i\theta }-e^{-i\theta }}}\,$	$\operatorname {arccot} x={\frac {i\ln \left({\frac {i-x}{i+x}}\right)}{2}}\,$
$\operatorname {cis} \,\theta =e^{i\theta }\,$	$\operatorname {arccis} \,x={\frac {\ln x}{i}}\,$

Miscel·lànies

Nucli de Dirichlet

El nucli de Dirichlet D_n(x) és la funció que apareix als dos cantons de la següent identitat:

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right\rbrack }{\sin \left({\frac {x}{2}}\right)}}.$

La convolució de qualsevol funció integrable de període 2π amb el nucli de Dirichlet coincideix amb l'aproximació en sèrie de Fourier de la funció de grau n. El mateix es compleix amb qualsevol mesura o distribució (matemàtiques)distribució.

Extensió de les fórmules de l'angle meitat

Si s'estableix

$t=\tan \left({\frac {x}{2}}\right),$

llavors

$\sin(x)={\frac {2t}{1+t^{2}}}$

i

$\cos(x)={\frac {1-t^{2}}{1+t^{2}}}$

i

$e^{ix}={\frac {1+it}{1-it}}.$

on e^ix és el mateix que cis(x).

Aquesta substitució de t per tan(x/2), amb la consegüent substitució de sin(x) per 2t/(1 + t²) i cos(x) per (1 − t²)/(1 + t²) és útil en càlcul per a transformar funcions racionals en sin(x) i cos(x) en funcions de t amb l'objectiu de trobar les seves primitives. Per a més informació vegeu fórmula de l'angle meitat de la tangent.

Vegeu també

• Trigonometria
• Demostració de les identitats trigonomètriques
• Aplicacions de la trigonometria
• Fórmula de la tangent de l'angle meitat
• Teorema del cosinus
• Teorema del sinus
• Teorema de la tangent
• Teorema de Pitàgores
• Constants trigonomètriques exactes
• Derivades de les funcions trigonomètriques
• Funció hiperbòlica