Mètode de quadres analítics

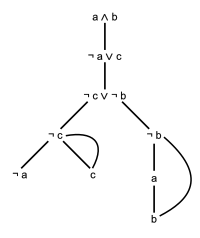
En la teoria de la prova, el quadre semàntic,^[1] també anomenat quadre analític, ^[2] arbre de la veritat, ^[1] o simplement arbre, ^[2] és un procediment de decisió per a lògiques oracionals i relacionades, i un procediment de demostració per a fórmules de lògica de primer ordre.^[1] Un quadre analític és una estructura d'arbre calculada per a una fórmula lògica, que té a cada node una subfórmula de la fórmula original per demostrar o refutar. La computació construeix aquest arbre i l'utilitza per demostrar o refutar tota la fórmula. ^[3] El mètode del quadre també pot determinar la satisfacció de conjunts finits de fórmules de diverses lògiques. És el procediment de prova més popular per a lògiques modals. ^[4]

Un mètode d'arbres de veritat conté un conjunt fix de regles per produir arbres a partir d'una fórmula lògica determinada, o conjunt de fórmules lògiques. Aquests arbres tindran més fórmules a cada branca i, en alguns casos, una branca pot arribar a contenir tant una fórmula com la seva negació, és a dir, una contradicció. En aquest cas, es diu que la branca es tanca.^[5] Si totes les branques d'un arbre es tanquen, es diu que el mateix arbre es tanca. En virtut de les regles per a la construcció de quadres, un arbre tancat és una prova que la fórmula original, o conjunt de fórmules, utilitzada per construir-la era en si mateixa contradictòria ^[5] i, per tant, falsa. Per contra, un quadre també pot demostrar que una fórmula lògica és tautòloga: si una fórmula és tautòloga, la seva negació és una contradicció, de manera que es tancarà un quadre construït a partir de la seva negació.^[5]

Història

A la seva Lògica simbòlica Part II, Charles Lutwidge Dodgson (també conegut pel seu pseudònim literari, Lewis Carroll) va introduir el mètode dels arbres, el primer ús modern d'un arbre de la veritat. ^[6]

El mètode dels quadres semàntics va ser inventat pel lògic holandès Evert Willem Beth (Beth 1955) ^[7] i simplificat, per a la lògica clàssica, per Raymond Smullyan (Smullyan 1968, 1995). ^[8] La simplificació de Smullyan, "taula unilateral", es descriu aquí. Walter Carnielli (Carnielli 1987) ha generalitzat el mètode de Smullyan a lògiques proposicionals i de primer ordre arbitràries de molts valors. ^[9]

Tableaux es pot veure intuïtivament com sistemes seqüents cap per avall. Aquesta relació simètrica entre quadres i sistemes seqüents es va establir formalment a (Carnielli 1991). ^[10]

Lògica proposicional

Rerefons

Una fórmula en lògica proposicional consta de lletres, que representen proposicions, i connectius per a conjunció, disjunció, condicionals, bicondicionals i negació. La veritat o la falsedat d'una proposició s'anomena valor de veritat. Es diu que una fórmula, o conjunt de fórmules, és satisfacible si hi ha una possible assignació de valors de veritat a les lletres proposicionals de manera que tota la fórmula, que combina les lletres amb connectius, també és certa.^[11] Es diu que aquesta assignació satisfà la fórmula.^[12]

Un quadre comprova si un conjunt de fórmules donat és satisfacible o no. Es pot utilitzar per comprovar la validesa o la implicació: una fórmula és vàlida si la seva negació no és satisfactòria i les fórmules $A_{1},\ldots ,A_{n}$ implicar $B$ si $\{A_{1},\ldots ,A_{n},\neg B\}$ és insatisfactori.

La taula següent mostra algunes variants de notació per a connectius lògics, per als lectors que poden estar més familiaritzats amb una notació diferent de la que s'utilitza aquí. En general, a partir del moment de la inclusió d'aquesta frase, en el text d'aquest article s'ha utilitzat el primer símbol de cada línia; tanmateix, com que els editors de la Viquipèdia no estan obligats a utilitzar una notació coherent dins o entre els articles, això pot canviar.^[13]

Connectiu	Símbol
AND	$A\land B$ , $A\cdot B$ , $AB$ , $A\&B$ , $A\&\&B$
equivalent	$A\equiv B$ , $A\Leftrightarrow B$ , $A\leftrightharpoons B$
implies	$A\Rightarrow B$ , $A\supset B$ , $A\rightarrow B$
NAND	$A{\overline {\land }}B$ , $A\mid B$ , ${\overline {A\cdot B}}$
no equivalent	$A\not \equiv B$ , $A\not \Leftrightarrow B$ , $A\nleftrightarrow B$
NOR	$A{\overline {\lor }}B$ , $A\downarrow B$ , ${\overline {A+B}}$
NOT	$\neg A$ , $-A$ , ${\overline {A}}$ , $\sim A$
OR	$A\lor B$ , $A+B$ , $A\mid B$ , $A\parallel B$
XNOR	$A$ XNOR $B$
XOR	$A{\underline {\lor }}B$ , $A\oplus B$

Mètode general

El principi principal dels quadres proposicionals és intentar "descompondre" fórmules complexes en altres més petites fins que es produeixin parells de literals complementaris o no sigui possible una altra expansió.

El mètode funciona en un arbre els nodes del qual estan etiquetats amb fórmules. A cada pas, aquest arbre es modifica; en el cas proposicional, els únics canvis permesos són les addicions d'un node com a descendent d'una fulla. El procediment comença generant l'arbre fet d'una cadena de totes les fórmules del conjunt per demostrar la insatisfacció. Aleshores, el següent procediment es pot aplicar repetidament de manera no determinística:

Trieu un node de fulla oberta. (El node fulla de la cadena inicial està marcat com obert).
Trieu un node aplicable a la branca que hi ha a sobre del node seleccionat.
Apliqueu el node aplicable, que correspon a expandir l'arbre per sota del node full seleccionat en funció d'alguna regla d'expansió (que es detalla a continuació).
Per a cada node de creació recent que sigui alhora un literal/negat i el complement del qual aparegui en un node anterior de la mateixa branca, marqueu la branca com a tancada. Marqueu tots els altres nodes creats recentment com a oberts.

Finalment, aquest procediment finalitzarà, perquè en algun moment s'apliquen tots els nodes aplicables i les regles d'expansió garanteixen que cada node de l'arbre sigui més senzill que el node aplicable utilitzat per crear-lo.

El principi del quadre és que les fórmules dels nodes de la mateixa branca es consideren conjuntament mentre que les diferents branques es consideren disjuntives. Com a resultat, un quadre és una representació en forma d'arbre d'una fórmula que és una disjunció de conjuncions. Aquesta fórmula és equivalent al conjunt per demostrar la insatisfacció. El procediment modifica el quadre de manera que la fórmula representada pel quadre resultant sigui equivalent a l'original. Una d'aquestes conjuncions pot contenir un parell de literals complementaris, en aquest cas es demostra que aquesta conjunció no és satisfactòria. Si es demostren que totes les conjuncions no són satisfactoris, el conjunt original de fórmules no és satisfactori.

Referències

↑ ^1,0 ^1,1 ^1,2 Howson, Colin. Logic with trees: an introduction to symbolic logic (en anglès). London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.
↑ ^2,0 ^2,1 Restall, Greg. Logic: an introduction (en anglès). London; New York: Routledge, 2006, p. 5, 42, 55 (Fundamentals of philosophy). ISBN 978-0-415-40067-1. OCLC ocm63115330.
↑ Howson, 2005, p. 27.
↑ Girle, 2014.
↑ ^5,0 ^5,1 ^5,2 Howson, Colin. Logic with trees: an introduction to symbolic logic (en anglès). London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.
↑ The Encyclopedia of Philosophy, 2023.
↑ Beth, 1955.
↑ Smullyan, 1995.
↑ Carnielli, 1987.
↑ Carnielli, 1991.
↑ Howson, Colin. Logic with trees: an introduction to symbolic logic. London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.
↑ Restall, Greg. Logic: an introduction (en anglès). London; New York: Routledge, 2006, p. 5, 42, 55 (Fundamentals of philosophy). ISBN 978-0-415-40067-1. OCLC ocm63115330.
↑ «Analytic Tableaux» (en anglès). [Consulta: 1r febrer 2025].

[:1-1] 1,0 ^1,1 ^1,2 Howson, Colin. Logic with trees: an introduction to symbolic logic (en anglès). London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.

[:0-2] 2,0 ^2,1 Restall, Greg. Logic: an introduction (en anglès). London; New York: Routledge, 2006, p. 5, 42, 55 (Fundamentals of philosophy). ISBN 978-0-415-40067-1. OCLC ocm63115330.

[FOOTNOTEHowson200527-3] Howson, 2005, p. 27.

[FOOTNOTEGirle2014-4] Girle, 2014.

[:12-5] 5,0 ^5,1 ^5,2 Howson, Colin. Logic with trees: an introduction to symbolic logic (en anglès). London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.

[FOOTNOTEThe_Encyclopedia_of_Philosophy2023-6] The Encyclopedia of Philosophy, 2023.

[FOOTNOTEBeth1955-7] Beth, 1955.

[FOOTNOTESmullyan1995-8] Smullyan, 1995.

[FOOTNOTECarnielli1987-9] Carnielli, 1987.

[FOOTNOTECarnielli1991-10] Carnielli, 1991.

[:13-11] Howson, Colin. Logic with trees: an introduction to symbolic logic. London; New York: Routledge, 1997, p. ix, x,24–29, 47. ISBN 978-0-415-13342-5.

[:02-12] Restall, Greg. Logic: an introduction (en anglès). London; New York: Routledge, 2006, p. 5, 42, 55 (Fundamentals of philosophy). ISBN 978-0-415-40067-1. OCLC ocm63115330.

[13] «Analytic Tableaux» (en anglès). [Consulta: 1r febrer 2025].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]