Models quantitatius del potencial d'acció
Els models quantitatius del potencial d'acció són eines matemàtiques i computacionals utilitzades per descriure i analitzar el comportament dels potencials d'acció en les cèl·lules excitables, com les neurones i les cèl·lules musculars. Un potencial d'acció és una variació ràpida i transitory de la membrana cel·lular que permet la propagació de senyals elèctrics al llarg de les cèl·lules, essencials per a la comunicació neuronal i la contracció muscular.
Els models quantitatius ajuden a entendre com els diferents factors, com la concentració d'ions, la resistència de la membrana i les propietats de les proteïnes i canals iònics, afecten la generació i la propagació dels potencials d'acció. Un dels models més coneguts és el model de Hodgkin-Huxley, que descriu matemàticament les dinàmiques del potencial d'acció a través d'equacions diferencials que reflecteixen els moviments d'ions a través de la membrana cel·lular. Aquests models són essencials per a la recerca en neurociència, fisiologia i en el desenvolupament de teràpies per a trastorns relacionats amb la conducció dels senyals elèctrics a les cèl·lules.
Tipus
[modifica]
En neurofisiologia, s'han desenvolupat diversos models matemàtics del potencial d'acció, que es divideixen en dos tipus bàsics. El primer tipus busca modelar quantitativament les dades experimentals, és a dir, reproduir exactament les mesures de corrent i tensió. El famós model Hodgkin-Huxley de l'axó del calamar Loligo exemplifica aquests models.[1] Encara que qualitativament correcte, el model HH no descriu tots els tipus de membrana excitable amb precisió, ja que només considera dos ions (sodi i potassi), cadascun amb només un tipus de canal sensible al voltatge. Tanmateix, altres ions com el calci poden ser importants i hi ha una gran diversitat de canals per a tots els ions.[2] Com a exemple, el potencial d'acció cardíac il·lustra com es poden generar potencials d'acció amb formes diferents a membranes amb canals de calci sensibles al voltatge i diferents tipus de canals de sodi/poassi. El segon tipus de model matemàtic és una simplificació del primer tipus; l'objectiu no és reproduir les dades experimentals, sinó entendre qualitativament el paper dels potencials d'acció en els circuits neuronals. Amb aquesta finalitat, els models fisiològics detallats poden ser innecessàriament complicats i poden enfosquir el "bosc per als arbres". El model FitzHugh-Nagumo és típic d'aquesta classe, que sovint s'estudia pel seu comportament d'entrament.[3] L'arrossegament s'observa habitualment a la natura, per exemple en la il·luminació sincronitzada de luciopers, que està coordinada per un esclat de potencials d'acció; [4] L'entrament també es pot observar en neurones individuals.[5] Ambdós tipus de models es poden utilitzar per entendre el comportament de petites xarxes neuronals biològiques, com ara els generadors de patrons centrals responsables d'algunes accions reflexes automàtiques.[6] Aquestes xarxes poden generar un patró temporal complex de potencials d'acció que s'utilitza per coordinar les contraccions musculars, com les implicades en la respiració o la natació ràpida per escapar d'un depredador.
Model Hodgkin-Huxley
[modifica]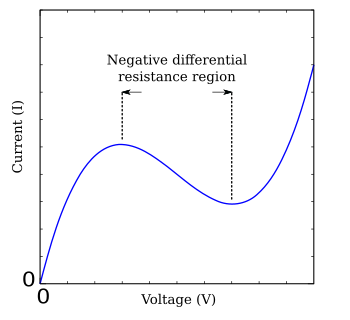
L'any 1952, Alan Lloyd Hodgkin i Andrew Huxley van desenvolupar un conjunt d'equacions per adaptar-se a les seves dades experimentals de pinça de tensió a la membrana axonal.[7][8] El model assumeix que la capacitat de membrana C és constant; així, la tensió transmembrana V canvia amb el corrent transmembrana total I tot segons l'equació
on INa, IK i IL són corrents transportades pels canals locals de sodi, canals de potassi i canals de "fuites" (un catch-all), respectivament. El terme inicial I ext representa el corrent que arriba de fonts externes, com els potencials postsinàptics excitatoris de les dendrites o l'elèctrode d'un científic.
Model FitzHugh-Nagumo
[modifica]A causa de la complexitat de les equacions de Hodgkin-Huxley, s'han desenvolupat diverses simplificacions que mostren un comportament qualitativament similar.[9][10] El model FitzHugh-Nagumo és un exemple típic d'aquest sistema simplificat.[11][12] Basat en el díode del túnel, el model FHN només té dues variables independents, però presenta un comportament d'estabilitat similar al de les equacions completes de Hodgkin-Huxley.[13] Les equacions són
on g(V) és una funció de la tensió V que té una regió de pendent negatiu al mig, flanquejada per un màxim i un mínim (figura FHN). Un cas senzill molt estudiat del model FitzHugh-Nagumo és el model del nervi Bonhoeffer-van der Pol, que es descriu per les equacions [14]
Referències
[modifica]- ↑ Hodgkin AL, Huxley AF, Katz B Journal of Physiology, 116, 4, 1952, pàg. 424–448. DOI: 10.1113/jphysiol.1952.sp004717. PMC: 1392213. PMID: 14946713.Hodgkin AL, Huxley AF Journal of Physiology, 116, 4, 1952, pàg. 449–472. DOI: 10.1113/jphysiol.1952.sp004717. PMC: 1392213. PMID: 14946713.Hodgkin AL, Huxley AF J Physiol, 116, 4, 1952, pàg. 473–496. DOI: 10.1113/jphysiol.1952.sp004718. PMC: 1392209. PMID: 14946714.Hodgkin AL, Huxley AF J Physiol, 116, 4, 1952, pàg. 497–506. DOI: 10.1113/jphysiol.1952.sp004719. PMC: 1392212. PMID: 14946715.Hodgkin AL, Huxley AF J Physiol, 117, 4, 1952, pàg. 500–544. DOI: 10.1113/jphysiol.1952.sp004764. PMC: 1392413. PMID: 12991237.
- ↑ Yamada WM, Koch C, Adams PR. «Multiple Channels and Calcium Dynamics». A: C. Koch, I Segev. Methods in Neuronal Modeling: From Synapses to Networks (en anglès). Cambridge, Massachusetts: Bradford Book, The MIT Press, 1989, p. 97–133. ISBN 978-0-262-11133-1.
- ↑ Hoppensteadt FC. An introduction to the mathematics of neurons (en anglès). Cambridge: Cambridge University Press, 1986. ISBN 978-0-521-31574-6.
- ↑ Hanson, F.E.; Case, J.F.; Buck, E.; Buck, J. Science, 174, 4005, 1971, pàg. 161–164. Bibcode: 1971Sci...174..161H. DOI: 10.1126/science.174.4005.161. PMID: 17742039.
- ↑ J. Membr. Biol., 56, 1, 1980, pàg. 9–18. DOI: 10.1007/BF01869347. PMID: 7441721.
- ↑ Getting PA. «Reconstruction of Small Neural Networks». A: C Koch and I Segev. Methods in Neuronal Modeling: From Synapses to Networks (en anglès). Cambridge, Massachusetts: Bradford Book, The MIT Press, 1989, p. 171–194. ISBN 978-0-262-11133-1.
- ↑ Hodgkin AL, Huxley AF, Katz B Journal of Physiology, 116, 4, 1952, pàg. 424–448. DOI: 10.1113/jphysiol.1952.sp004717. PMC: 1392213. PMID: 14946713.Hodgkin AL, Huxley AF Journal of Physiology, 116, 4, 1952, pàg. 449–472. DOI: 10.1113/jphysiol.1952.sp004717. PMC: 1392213. PMID: 14946713.Hodgkin AL, Huxley AF J Physiol, 116, 4, 1952, pàg. 473–496. DOI: 10.1113/jphysiol.1952.sp004718. PMC: 1392209. PMID: 14946714.Hodgkin AL, Huxley AF J Physiol, 116, 4, 1952, pàg. 497–506. DOI: 10.1113/jphysiol.1952.sp004719. PMC: 1392212. PMID: 14946715.Hodgkin AL, Huxley AF J Physiol, 117, 4, 1952, pàg. 500–544. DOI: 10.1113/jphysiol.1952.sp004764. PMC: 1392413. PMID: 12991237.
- ↑ «The Hodgkin–Huxley Model». A: The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System (en anglès). New York: Springer Verlag, 1994, p. 29–49.
- ↑ Hoppensteadt FC. An introduction to the mathematics of neurons (en anglès). Cambridge: Cambridge University Press, 1986. ISBN 978-0-521-31574-6.
- ↑ FitzHugh R J. Gen. Physiol., 43, 5, 1960, pàg. 867–896. DOI: 10.1085/jgp.43.5.867. PMC: 2195039. PMID: 13823315. Biological Cybernetics, 66, 5, 1992, pàg. 381–387. DOI: 10.1007/BF00197717. PMID: 1562643.
- ↑ FitzHugh R Biophysical Journal, 1, 6, 1961, pàg. 445–466. Bibcode: 1961BpJ.....1..445F. DOI: 10.1016/S0006-3495(61)86902-6. PMC: 1366333. PMID: 19431309.
- ↑ Proceedings of the IRE, 50, 10, 1962, pàg. 2061–2070. DOI: 10.1109/JRPROC.1962.288235.
- ↑ FitzHugh R. «Mathematical models of axcitation and propagation in nerve». A: HP Schwann. Biological Engineering (en anglès). New York: McGraw-Hill, 1969, p. 1–85.
- ↑ Bonhoeffer KF J. Gen. Physiol., 32, 1, 1948, pàg. 69–91. DOI: 10.1085/jgp.32.1.69. PMC: 2213747. PMID: 18885679.Bonhoeffer KF Naturwissenschaften, 40, 11, 1953, pàg. 301–311. Bibcode: 1953NW.....40..301B. DOI: 10.1007/BF00632438.van der Pol B Philosophical Magazine, 2, 1926, pàg. 978–992.van der Pol B, van der Mark J Philosophical Magazine, 6, 1928, pàg. 763–775.van der Pol B, van der Mark J Arch. Neerl. Physiol., 14, 1929, pàg. 418–443.



