Principi d'inclusió-exclusió

Exemple d'inclusió-exclusió a partir de tres conjunts.

En combinatòria, el principi d'inclusió-exclusió permet expressar el nombre d'elements (o cardinal) d'una unió finita de conjunts finits en funció del nombre d'elements d'aquests conjunts i de les seves interseccions. Es tradueix directament en termes de probabilitats.

S'atribueix al matemàtic Abraham De Moivre, tot i que va ser formulat per primera vegada pel matemàtic portuguès Daniel Augusto da Silva (1814-1878) i va ser generalitzat per Camille Jordan, i es coneix també (ell o la seva versió probabilista) sota el nom de fórmula del garbell de Poincaré, fórmula de Poincaré, o fórmula del garbell.

El cas dos conjunts

Exemple

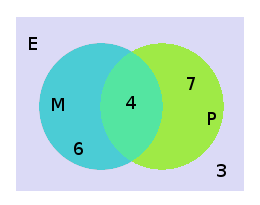
Entre 20 estudiants, 10 estudien les matemàtiques, 11 estudien la física, i 4 estudien les dues assignatures al mateix temps. Quants n'hi ha d'estudiants que no estudien ni matemàtiques ni física?

Per visualitzar-ho es pot construir un diagrama de Venn.

S'encerclen els elements que verifiquen la mateixa propietat. E representa el grup de tots els estudiants, M representa els que tenen la propietat d'«estudiar matemàtiques», P representa aquells que posseeix la propietat: d'«estudiar física».

Es col·loca a cada part el nombre d'estudiants. Atès que quatre persones estudien a la vegada matemàtiques i física, se'n posen 4 en la intersecció dels dos cercles. Hi ha d'haver per tant 10-4=6 persones que estudien matemàtiques però no física i 11-4=7 persones que estudien física però no matemàtiques. Queden per tant 20-(6+4+7)=3 persones que no estudien ni matemàtiques ni física.

Aquest resultat es troba fàcilment emprant el principi d'inclusió-exclusió que dona el nombre d'estudiants que no posseeixen aquestes dues propietats 20-10-11+4=3.

Fórmula per a n = 2

Siguin A i B dos conjunts finits, la fórmula s'escriu

$|A\cup B|=|A|+|B|-|A\cap B|$

on|A| i|B | representen els cardinals respectius de A i B.

En Altres Paraules, es poden comptar els elements de la unió de dos conjunts A i B sumant els cardinals d'aquests dos conjunts i sostraient el cardinal de la seva intersecció.

Cas general

Siguin A ₁..., A _n n conjunts finits. Es té

$\left|\,\bigcup _{i=1}^{n}A_{i}\,\right|=\sum _{i=1}^{n}\left|A_{i}\right|-\sum _{(i,j)\,/\,1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|$$+\sum _{(i,j,k)\,/\,1\leq i<j<k\leq n}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \cdots \cdots \ +(-1)^{n+1}|A_{1}\cap \ldots \cap A_{n}|$

on|A| designa el cardinal d'un conjunt finit A.

Aquesta fórmula es també pot escriure de manera més condensada

$\left|\,\bigcup _{i=1}^{n}A_{i}\,\right|=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{1\leq i_{1}<i_{2}<\ldots <i_{k}\leq n}\left|A_{i_{1}}\cap A_{i_{2}}\cap \ldots \cap A_{i_{k}}\right|\right)$.

Es pot demostrar per inducció sobre n, o fent servir les funcions característiques.

Sigui E un conjunt finit, que conté els conjunts A _i. Es dedueix per pas al complementari que el cardinal del conjunt dels elements de E que no pertanyen a cap dels A_i és:

$\left|E\setminus \bigcup _{i=1}^{n}A_{i}\,\right|=|E|+\sum _{k=1}^{n}\left((-1)^{k}\sum _{1\leq i_{1}<i_{2}<\ldots <i_{k}\leq n}\left|A_{i_{1}}\cap A_{i_{2}}\cap \ldots \cap A_{i_{k}}\right|\right)$.

El principi d'inclusió-exclusió es pot deduir de la fórmula d'inversió de Möbius.

Versió probabilista

Siguin un espai de probabilitat $\scriptstyle \ (\Omega ,{\mathcal {A}},\mathbb {P} )\$ i $\scriptstyle \ n\$ elements $\scriptstyle \ A_{1},A_{2},\dots ,A_{n}\$ de la tribu $\scriptstyle \ {\mathcal {A}}.\$ es té

$\mathbb {P} \left(\,\bigcup _{i=1}^{n}A_{i}\,\right)=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{1\leq i_{1}<i_{2}<\ldots <i_{k}\leq n}\mathbb {P} \left(A_{i_{1}}\cap A_{i_{2}}\cap \ldots \cap A_{i_{k}}\right)\right)$.

Aquesta fórmula es pot demostrar per inducció sobre n, o fent servir funcions característiques, de la mateixa manera que la fórmula precedent. També es pot formular de la manera següent:

$\mathbb {P} \left(\,\bigcup _{i=1}^{n}A_{i}\,\right)=\sum _{S\subset [\![1,n]\!],\,S\neq \varnothing }(-1)^{-1+|S|}\ \mathbb {P} \left(\bigcap _{i\in S}\,A_{i}\right)$.

Aplicacions

Desigualtats de Bonferroni

El terme d'ordre k de la suma decreix (en valor absolut) en funció de k. Les sumes parcials dels primers termes de la fórmula subministren per tant alternativament a un augmentant i a un minorant la suma completa, i es poden fer servir com aproximacions d'aquesta: aquests augmentants i minorants s'anomenen les desigualtats de Bonferroni.

Desarranjaments i nombre de punts fixos d'una permutació

En combinatòria, la fórmula del garbell permet determinar el nombre de desarranjaments d'un conjunt finit. Un desarranjament d'un conjunt A és una bijection de A en si mateix sense punt fix. Gràcies al principi d'inclusió-exclusió de Moivre, es pot demostrar que si el cardinal de A és igual a n, llavors el nombre de desarranjaments de A és el nombre sencer més proper a n!/e (on e designa la base dels logaritmes neperians). En resulta que si totes les bijeccions tenen la mateixa probabilitat de ser escollides, llavors la probabilitat perquè una bijecció presa a l'atzar sigui un desarranjament tendeix ràpidament cap a 1/e quan n tendeix cap a l'infinit.

Es pot portar més lluny l'estudi estadístic dels punts fixos de les permutacions. notant N(ω) el nombre de punts fixos d'una permutació ω. S'observa que N(ω)=0 si i només si ω és un desarranjament. En això la proposició següent precisa el resultat en relació amb els desarranjaments (que no és altre que el càlcul de $\scriptstyle \ \mathbb {P} \left(\,N=0\right)\$):

Proposició Per a tot enter k comprès entre 0 i n $\mathbb {P} \left(\,N=k\right)\ =\ {\frac {1}{k!}}\quad \sum _{\ell =0}^{n-k}\ {\frac {(-1)^{\ell }}{\ell !}}.$

En particular, la llei de N és molt propera a la llei de Poisson de paràmetre 1, per a n gran. Això il·lustra el paradigma de Poisson, segons el qual una suma d'un gran nombre de variables de Bernouilli de petit paràmetre, poc correlacionades, segueix aproximadament la Llei de Poisson: N pot ser vista com tal suma. L'escriptura de N com a suma de variables de Bernoulli permet un càlcul ràpid de l'esperança i de la variància de N, el que l'expressió explicita de la llei de N, donada damunt, no permet.

Demostració

L'espai de probabilitat $\scriptstyle \ (\Omega ,{\mathcal {A}},\mathbb {P} )\$ és aquí el conjunt finit $\scriptstyle \ \Omega ={\mathfrak {S}}_{n}\$ de les permutacions de $\scriptstyle \ [\![1,n]\!],\$ proveït de la Σ-àlgebra trivial i de la llei uniforme. L'esdeveniment A_k és el conjunt de les permutacions que deixen l'enter k invariant. Per a una part S de $\scriptstyle \ [\![1,n]\!],\$ es nota A_S el conjunt de les permutacions de Ω que deixen tots els elements de S invariants. Així $\bigcup _{i=1}^{n}A_{i}\,=\,\left\{N\geq 1\right\}\quad {\text{et}}\quad A_{S}=\bigcap _{i\in S}A_{i}.$

Via l'aplicació que, a una permutació ω de $\scriptstyle \ {\mathfrak {S}}_{n},\$ associa la seva restricció a la subclasse $\scriptstyle \ [\![1,n]\!]\backslash S,\$ A_S és en bijection amb el conjunt de les permutacions de $\scriptstyle \ [\![1,n]\!]\backslash S,\$ per tant el cardinal de A_S és (n-#S)!. Per tant, la probabilitat de A_S és (n-#S)!/(n!). La fórmula d'inclusió-exclusió, sota la seva forma probabilista, s'escriu llavors

$\mathbb {P} \left(\,N\geq 1\right)=\sum _{S\subset [\![1,n]\!],\,S\neq \varnothing }(-1)^{1+\#S}\ \mathbb {P} \left(A_{S}\right).$

Reagrupant les $\scriptstyle \ {n \choose k}\$ parts S d'igual cardinal k, ja que la probabilitat de A_S no depèn més que del cardinal de S, s'obté

$\mathbb {P} \left(\,N\geq 1\right)=\sum _{k=1}^{n}(-1)^{k+1}\ {n \choose k}{\frac {n-k!}{n!}}\ =\ \sum _{k=1}^{n}\ {\frac {(-1)^{k+1}}{k!}},$

després

$\mathbb {P} \left(\,N=0\right)\ =\ \sum _{k=0}^{n}\ {\frac {(-1)^{k}}{k!}}.$

Es nota d_n aquesta última probabilitat, que és la probabilitat que una permutació de $\scriptstyle \ {\mathfrak {S}}_{n}\$ sigui un desarranjament: d_n s'obté truncant el desenvolupament en sèrie de 1/e just després del terme d'índex n (el que, entre parèntesis, és una manera, entre altres, de justificar la convenció d₀ = 1). Per a una part S de $\scriptstyle \ [\![1,n]\!],\$ es nota B_S el conjunt de les permutacions de Ω el conjunt dels punts fixos del qual és exactament S: B_S és en bijecció amb el conjunt dels desarranjaments de $\scriptstyle \ [\![1,n]\!]\backslash S,\$ per tant el cardinal de B_S és (n-#S)! d_n-#S. Així

$\mathbb {P} \left(\,N=k\right)=\sum _{\#S=k}\mathbb {P} \left(\,B_{S}\right)\ =\ {n \choose k}\ {\frac {n-k!\,d_{n-k}}{n!}}\ =\ {\frac {d_{n-k}}{k!}}\ \simeq \ {\frac {e^{-1}}{k!}}.$

Ara bé, per definició, una variable aleatòria X segueix la llei de Poisson de paràmetre a, per a tot k enter positiu o nul,

$\mathbb {P} \left(\,X=k\right)={\frac {a^{k}\,e^{-a}}{k!}}.$ El nombre de desarranjaments de A és el nombre enter més proper a n!/e gràcies a una majorant (en valor absolut) de la resta d'una sèrie alternada pel primer terme d'aquesta resta, en el cas on els valors absoluts dels termes d'una sèrie alternada formen una successió decreixent