Vés al contingut

Pticografia

De la Viquipèdia, l'enciclopèdia lliure
Collection of a ptychographic imaging data set in the simplest single-aperture configuration.
Recollida d'un conjunt de dades d'imatges psicogràfiques en la configuració d'obertura única més senzilla. (a) L'incident d'il·luminació coherent des de l'esquerra es limita localment a una àrea de l'exemplar. Un detector aigües avall de la mostra registra un patró d'interferència. (b) L'exemplar es desplaça (en aquest cas, cap amunt) i es registra un segon patró. Tingueu en compte que les regions d'il·luminació s'han de solapar entre elles per facilitar la restricció de la invariància del canvi psicogràfic. (c) Tot un conjunt de dades psicogràfiques utilitza moltes regions d'il·luminació superposades. (d) Tot el conjunt de dades és de quatre dimensions: per a cada posició d'il·luminació 2D (x,y), hi ha un patró de difracció 2D (kx,ky).

Pticografia (/t(ʌ)ɪˈkogræfi/ t(ʌ)i-KO-graf-ee) és un mètode computacional d'imatges microscòpiques.[1] Genera imatges processant molts patrons d'interferència coherents que s'han dispersat des d'un objecte d'interès. La seva característica definitòria és la invariància translacional, que significa que els patrons d'interferència són generats per una funció constant (per exemple, un camp d'il·luminació o una parada d'obertura) que es mou lateralment en una quantitat coneguda respecte a una altra funció constant (l'espècimen en si o un camp d'ona). Els patrons d'interferència es produeixen a una certa distància d'aquests dos components, de manera que les ones disperses s'estenen i es "pleguen" (grec antic: πτύξ és 'plegar' [2]) l'un a l'altre tal com es mostra a la figura.

La pticografia es pot utilitzar amb llum visible, raigs X, ultraviolat extrem (EUV) o electrons. A diferència de les imatges de lents convencionals, la pticografia no es veu afectada per les aberracions induïdes per la lent o els efectes de difracció causats per una obertura numèrica limitada. Això és especialment important per a la imatge de longitud d'ona a escala atòmica, on és difícil i costós fer lents de bona qualitat amb una obertura numèrica alta. Un altre avantatge important de la tècnica és que permet veure amb molta claredat els objectes transparents. Això es deu al fet que és sensible a la fase de la radiació que ha travessat una mostra i, per tant, no es basa en el fet que l'objecte absorbeixi la radiació. En el cas de la microscòpia biològica de llum visible, això significa que les cèl·lules no s'han de tacar ni etiquetar per crear contrast.

Fase de recuperació

[modifica]

Tot i que els patrons d'interferència utilitzats en la pticografia només es poden mesurar en intensitat, les limitacions matemàtiques que ofereix la invariància translacional de les dues funcions (il·luminació i objecte), juntament amb els desplaçaments coneguts entre elles, fan que es pugui recuperar la fase del camp d'ona. mitjançant un càlcul invers. Per tant, la pticografia proporciona una solució integral a l'anomenat "problema de fase". Un cop aconseguit això, s'ha recuperat tota la informació relativa a l'ona dispersa (mòdul i fase), i així es poden obtenir imatges pràcticament perfectes de l'objecte. Hi ha diverses estratègies per realitzar aquest càlcul de recuperació de fase inversa, inclosa la deconvolució de distribució Wigner directa (WDD) [3] i mètodes iteratius.[4][5][6][7][8] L'algoritme de mapa de diferències desenvolupat per Thibault i col·laboradors [7] està disponible en un paquet descarregable anomenat PtyPy.[9]

Configuracions òptiques

[modifica]

Hi ha moltes configuracions òptiques per a la pticografia: matemàticament, requereix dues funcions invariants que es mouen una a través de l'altra mentre es mesura un patró d'interferència generat pel producte de les dues funcions. El patró d'interferència pot ser un patró de difracció, un patró de difracció de Fresnel o, en el cas de la pticografia de Fourier, una imatge. La convolució "ptycho" en una imatge psicogràfica de Fourier derivada de la funció de resposta a l'impuls de la lent.

L'obertura única

[modifica]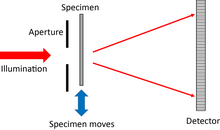
Diagram showing the optical configuration for ptychographu using a single aperture.
Configuració òptica per a la pticografia amb una sola obertura

Aquesta és conceptualment la disposició psicogràfica més senzilla.[10] El detector pot estar molt lluny de l'objecte (és a dir, en el pla de difracció de Fraunhofer), o més a prop, en el règim de Fresnel. Un avantatge del règim de Fresnel és que ja no hi ha un feix d'intensitat molt alta al centre del patró de difracció, que d'altra manera pot saturar els píxels del detector allà.

Pticografia de sonda focalitzada

[modifica]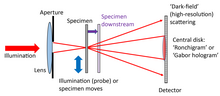
Diagram showing the optical configuration for ptychography using a focussed probe.
Configuració òptica per a la pticografia mitjançant una sonda focalitzada

S'utilitza una lent per formar un encreuament ajustat del feix d'il·luminació al pla de l'exemplar. La configuració s'utilitza en el microscopi electrònic de transmissió d'escaneig (STEM), [11][12] i sovint en la pticografia de raigs X d'alta resolució. De vegades, l'exemplar es desplaça cap amunt o aigües avall de l'encreuament de la sonda per permetre que s'augmenti la mida del pegat d'il·luminació, requerint així menys patrons de difracció per escanejar un camp de visió ampli.

Pticografia de camp proper

[modifica]
A diagram showing the optical configuration for near-field ptychography.
Configuració òptica per a la pticografia de camp proper

Això utilitza un ampli camp d'il·luminació. Per proporcionar un augment, un feix divergent incideix a l'espècimen. Una imatge desenfocada, que apareix com un patró d'interferència de Fresnel, es projecta al detector. La il·luminació ha de tenir distorsions de fase, sovint proporcionades per un difusor que agita la fase de l'ona incident abans d'arribar a l'exemplar, en cas contrari, la imatge es manté constant a mesura que es mou l'exemplar, de manera que no hi ha nova informació psicogràfica d'una posició a una altra. el següent.[13] Al microscopi electrònic, es pot utilitzar una lent per mapejar la imatge de Fresnel ampliada al detector.

Pticografia de Fourier

[modifica]
Diagram showing the optical configuration for Fourier ptychography.
Configuració òptica per a la pticografia de Fourier

S'utilitza un microscopi convencional amb una lent d'objectiu d'obertura numèrica relativament petita. L'exemplar s'il·lumina des d'una sèrie d'angles diferents. Els feixos paral·lels que surten de l'espècimen es focalitzen al pla focal posterior de la lent de l'objectiu, que és per tant un patró de difracció de Fraunhofer de l'ona de sortida de l'espècimen (teorema d'Abbe). La inclinació de la il·luminació té l'efecte de canviar el patró de difracció a través de l'obertura de l'objectiu (que també es troba al pla focal posterior). Ara s'aplica el principi d'invariància de desplaçament psicogràfic estàndard, excepte que el patró de difracció actua com a objecte i la parada del pla focal posterior actua com la funció d'il·luminació a la pticografia convencional. La imatge es troba en el pla de difracció de Fraunhofer d'aquestes dues funcions (una altra conseqüència del teorema d'Abbe), igual que en la pticografia convencional. L'única diferència és que el mètode reconstrueix el patró de difracció, que és molt més ampli que la limitació de parada d'obertura. S'ha de dur a terme una transformada de Fourier final per produir la imatge d'alta resolució. Tots els algorismes de reconstrucció utilitzats en la pticografia convencional s'apliquen a la pícografia de Fourier i, de fet, gairebé totes les extensions diverses de la pticografia convencional s'han utilitzat en la pícografia de Fourier.[14]

Pticografia d'imatge

[modifica]
Diagram showing the optical configuration for imaging ptychography.
Configuració òptica per a la pticografia d'imatges

Una lent s'utilitza per fer una imatge convencional. Una obertura en el pla d'imatge actua de manera equivalent a la il·luminació en la pticografia convencional, mentre que la imatge correspon a l'exemplar. El detector es troba al pla de difracció de Fraunhofer o Fresnel aigües avall de la imatge i l'obertura.[15]

Pticografia de Bragg o de reflexió

[modifica]
Diagram showing the optical configuration for reflection or Bragg ptychography.
Configuració òptica per reflexió o pticografia de Bragg

Aquesta geometria es pot utilitzar per mapejar característiques superficials o per mesurar la tensió en espècimens cristal·lins. Els desplaçaments a la superfície de la mostra, o els plans de Bragg atòmics perpendiculars a la superfície, apareixen en la fase de la imatge psicogràfica.[16][17][18]

Pticografia vectorial

[modifica]

La pticografia vectorial s'ha d'invocar quan el model multiplicatiu de la interacció entre la sonda i l'exemplar no es pot descriure per quantitats escalars.[19] Això passa normalment quan la llum polaritzada sondeja una mostra anisòtropa i quan aquesta interacció modifica l'estat de polarització de la llum. En aquest cas, la interacció ha de ser descrita pel formalisme de Jones, [20] on el camp i l'objecte es descriuen mitjançant un vector complex de dos components i una matriu complexa de 2×2, respectivament. La configuració òptica per a la pticografia vectorial és similar a la de la pticografia clàssica (escalar), encara que s'ha d'implementar un control de la polarització de la llum (abans i després de la mostra) a la configuració. Els mapes de Jones dels exemplars es poden recuperar, permetent la quantificació d'un ampli ventall de propietats òptiques (fase, birrefringència, orientació dels eixos neutres, diatenuació, etc.).[21] De manera similar a la pticografia escalar, les sondes utilitzades per a la mesura es poden estimar conjuntament amb la mostra.[22] Com a conseqüència, la pticografia vectorial també és un enfocament elegant per a la imatge quantitativa de feixos de llum vectorials coherents (mescla de front d'ona i característiques de polarització).[23]

Aplicacions

[modifica]

Les aplicacions de la pticografia són diverses perquè es pot utilitzar amb qualsevol tipus de radiació que es pugui preparar com una ona de propagació quasi monocromàtica.

Les imatges psicogràfiques, juntament amb els avenços en detectors i informàtica, han donat lloc al desenvolupament de microscopis de raigs X.[24][25] Es necessiten feixos coherents per obtenir patrons de difracció de camp llunyà amb patrons de taques. Els feixos de raigs X coherents es poden produir amb fonts modernes de radiació de sincrotró, làsers d'electrons lliures i fonts d'alta harmònica. Pel que fa a l'anàlisi rutinària, la ptotomografia de raigs X [26] és avui la tècnica més utilitzada. S'ha aplicat a molts problemes de materials incloent, per exemple, l'estudi de la pintura, [27] imatges de la química de les bateries, [28] capes apilades d'imatges de cèl·lules solars en tàndem, [29] i la dinàmica de la fractura.[30] En el règim de raigs X, també s'ha utilitzat la pticografia per obtenir un mapeig 3D de l'estructura desordenada de l'escarabat Cyphochilus blanc, [31] i una imatge en 2D de l'estructura del domini en una heterounió massiva per a cèl·lules solars de polímer.[32]

La pticografia de llum visible s'ha utilitzat per obtenir imatges de cèl·lules biològiques vives i estudiar-ne el creixement, la reproducció i la motilitat.[33] En la seva versió vectorial, també es pot utilitzar per mapejar propietats òptiques quantitatives de materials anisotròpics com els biominerals [34] o les metasuperfícies [35]

La pticografia electrònica és única (entre altres modes d'imatge d'electrons) sensible tant a àtoms pesats com lleugers simultàniament. S'ha utilitzat, per exemple, en l'estudi dels mecanismes de lliurament de fàrmacs de nanoestructura observant molècules de fàrmacs tacades per àtoms pesats dins de gàbies de nanotubs de carboni lleugers.[36] Amb els feixos d'electrons, els electrons de longitud d'ona més curta i d'energia més alta utilitzats per a imatges de major resolució poden causar danys a la mostra ionitzant-la i trencant enllaços, però la pticografia de feix d'electrons ara ha produït imatges rècord de bisulfur de molibdè amb una resolució de 0,039 nm utilitzant un feix d'electrons de menor energia i detectors que són capaços de detectar electrons individuals, de manera que els àtoms es poden localitzar amb més precisió.[37][38]

La pticografia té diverses aplicacions a la indústria dels semiconductors, inclosa la imatge de les seves superfícies utilitzant EUV, [39] la seva estructura a granel 3D mitjançant raigs X, [40] i el mapeig de camps de tensió mitjançant la pticografia de Bragg, per exemple, en nanofils.[41]

  • Patró de difracció d'un feix de raigs X que travessa un cristall estacionari. Els punts són àrees d'interferència constructiva; l'estructura atòmica del cristall es pot elaborar a partir del patró. A la pticografia, una mostra (que no necessita ser cristal·lina) es mou seqüencialment a través del feix, creant una sèrie de patrons de difracció.
    Patró de difracció d'un feix de raigs X que travessa un cristall estacionari. Els punts són àrees d'interferència constructiva; l'estructura atòmica del cristall es pot elaborar a partir del patró. A la pticografia, una mostra (que no necessita ser cristal·lina) es mou seqüencialment a través del feix, creant una sèrie de patrons de difracció.
  • Un picògraf de llum visible d'un objectiu de resolució òptica USAF, fet amb una obertura estenopeica en un tros de cartró. En els gràfics, la tonalitat representa la fase i el mòdul representa la luminància. (a) mostra una imatge única amb detalls de difracció complexos. (b) mostra la versió processada per ordinador de (a). (c) mostra el resultat de les dades combinades de difracció processades per ordinador després d'escanejar tota la mostra.
    Un picògraf de llum visible d'un objectiu de resolució òptica USAF, fet amb una obertura estenopeica en un tros de cartró. En els gràfics, la tonalitat representa la fase i el mòdul representa la luminància. (a) mostra una imatge única amb detalls de difracció complexos. (b) mostra la versió processada per ordinador de (a). (c) mostra el resultat de les dades combinades de difracció processades per ordinador després d'escanejar tota la mostra.
  • Pticografia de raigs X a una línia de llum de dispersió d'angle petit d'un sincrotró. Aquest picògraf de raigs X d'una placa de zona mostra les dades de lluminositat a la imatge (a) i les dades de fase a la imatge (b). Els requadres I, II i III de (b) es mostren a (i), (j) i (k) respectivament tal com es van processar l'any 2015; mostren una clara millora en la resolució respecte als algorismes utilitzats el 2008 mostrats a (l), (m) i (n).
    Pticografia de raigs X a una línia de llum de dispersió d'angle petit d'un sincrotró. Aquest picògraf de raigs X d'una placa de zona mostra les dades de lluminositat a la imatge (a) i les dades de fase a la imatge (b). Els requadres I, II i III de (b) es mostren a (i), (j) i (k) respectivament tal com es van processar l'any 2015; mostren una clara millora en la resolució respecte als algorismes utilitzats el 2008 mostrats a (l), (m) i (n).

Referències

[modifica]
  1. ↑ «Ptychography». A: Springer Handbook of Microscopy (en anglès). Springer International Publishing, 2019, p. 819–904 (Springer Handbooks). DOI 10.1007/978-3-030-00069-1_17. ISBN 978-3-030-00068-4. 
  2. ↑ (en alemany) Berichte der Bunsengesellschaft für physikalische Chemie, 74, 11, 1970, pàg. 1148–1154. DOI: 10.1002/bbpc.19700741112.
  3. ↑ Phil. Trans. R. Soc. Lond. A, 339, 1655, 15-06-1992, pàg. 521–553. Bibcode: 1992RSPTA.339..521R. DOI: 10.1098/rsta.1992.0050.
  4. ↑ Applied Physics Letters, 85, 20, 15-11-2004, pàg. 4795–4797. Bibcode: 2004ApPhL..85.4795R. DOI: 10.1063/1.1823034.
  5. ↑ Optics Express, 16, 10, 5-2008, pàg. 7264–78. Bibcode: 2008OExpr..16.7264G. DOI: 10.1364/OE.16.007264. PMID: 18545432 [Consulta: free].
  6. ↑ Science, 321, 5887, 7-2008, pàg. 379–82. Bibcode: 2008Sci...321..379T. DOI: 10.1126/science.1158573. PMID: 18635796.
  7. ↑ 7,0 7,1 Ultramicroscopy, 109, 4, 3-2009, pàg. 338–43. DOI: 10.1016/j.ultramic.2008.12.011. PMID: 19201540.
  8. ↑ Ultramicroscopy, 109, 10, 9-2009, pàg. 1256–62. DOI: 10.1016/j.ultramic.2009.05.012. PMID: 19541420.
  9. ↑ Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 472, 2196, 12-2016, pàg. 20160640. Bibcode: 2016RSPSA.47260640E. DOI: 10.1098/rspa.2016.0640. PMC: 5247528. PMID: 28119552.
  10. ↑ Ultramicroscopy, 107, 2–3, 2-2007, pàg. 227–231. DOI: 10.1016/j.ultramic.2006.07.007. PMID: 16959428.
  11. ↑ Ultramicroscopy, 48, 3, 3-1993, pàg. 304–314. DOI: 10.1016/0304-3991(93)90105-7. ISSN: 0304-3991.
  12. ↑ (en anglès) Nature Communications, 7, 8-2016, pàg. 12532. Bibcode: 2016NatCo...712532Y. DOI: 10.1038/ncomms12532. PMC: 5007440. PMID: 27561914.
  13. ↑ (en anglès) Scientific Reports, 3, 1, 31-05-2013, pàg. 1927. Bibcode: 2013NatSR...3E1927S. DOI: 10.1038/srep01927. PMC: 3668322. PMID: 23722622.
  14. ↑ (en anglès) Nature Photonics, 7, 9, 9-2013, pàg. 739–745. arXiv: 1405.0226. Bibcode: 2013NaPho...7..739Z. DOI: 10.1038/nphoton.2013.187. PMC: 4169052. PMID: 25243016.
  15. ↑ (en anglès) Scientific Reports, 5, 10-2015, pàg. 14690. Bibcode: 2015NatSR...514690M. DOI: 10.1038/srep14690. PMC: 4589788. PMID: 26423558.
  16. ↑ (en anglès) Nano Letters, 12, 10, 10-2012, pàg. 5148–5154. Bibcode: 2012NanoL..12.5148H. DOI: 10.1021/nl303201w. PMID: 22998744.
  17. ↑ (en anglès) Optica, 1, 1, 22-07-2014, pàg. 39–44. arXiv: 1312.2049. Bibcode: 2014Optic...1...39S. DOI: 10.1364/OPTICA.1.000039. ISSN: 2334-2536.
  18. ↑ Godard, P.; Carbone, G.; Allain, M.; Mastropietro, F.; Chen, G. (en anglès) Nature Communications, 2, 1, 2011, pàg. 568. DOI: 10.1038/ncomms1569. ISSN: 2041-1723. PMID: 22127064 [Consulta: free].
  19. ↑ (en anglès) Optics Letters, 40, 22, 11-2015, pàg. 5144–5147. Bibcode: 2015OptL...40.5144F. DOI: 10.1364/OL.40.005144. PMID: 26565820.
  20. ↑ (en anglès) JOSA, 31, 7, 01-07-1941, pàg. 488–493. DOI: 10.1364/JOSA.31.000488.
  21. ↑ (en anglès) Optics Letters, 43, 4, 2-2018, pàg. 763–766. arXiv: 1712.00260. Bibcode: 2018OptL...43..763F. DOI: 10.1364/OL.43.000763. PMID: 29443988.
  22. ↑ (en anglès) Optics Express, 27, 6, 3-2019, pàg. 8143–8152. Bibcode: 2019OExpr..27.8143B. DOI: 10.1364/OE.27.008143. PMID: 31052637 [Consulta: free].
  23. ↑ Optics Express, 28, 23, 11-2020, pàg. 35339–35349. Bibcode: 2020OExpr..2835339B. DOI: 10.1364/OE.408665. PMID: 33182982 [Consulta: free].
  24. ↑ Nature, 467, 7314, 9-2010, pàg. 409–410. Bibcode: 2010Natur.467..409C. DOI: 10.1038/467409a. PMID: 20864990.
  25. ↑ «Ptychography» (en anglès). www6.slac.stanford.edu. [Consulta: 29 juliol 2018].
  26. ↑ (en anglès) Nature, 467, 7314, 9-2010, pàg. 436–439. Bibcode: 2010Natur.467..436D. DOI: 10.1038/nature09419. PMID: 20864997.
  27. ↑ (en anglès) Scientific Reports, 3, 1, 31-01-2013, pàg. 1177. Bibcode: 2013NatSR...3E1177C. DOI: 10.1038/srep01177. PMC: 3558722. PMID: 23378910.
  28. ↑ Nature Photonics, 8, 10, 07-09-2014, pàg. 765–769. Bibcode: 2014NaPho...8..765S. DOI: 10.1038/nphoton.2014.207. ISSN: 1749-4885.
  29. ↑ Nanoscale, 7, 32, 8-2015, pàg. 13765–13774. Bibcode: 2015Nanos...713765P. DOI: 10.1039/C5NR02824H. PMID: 26220159.
  30. ↑ (en anglès) Advanced Engineering Materials, 17, 4, 10-02-2015, pàg. 545–553. DOI: 10.1002/adem.201400443. ISSN: 1438-1656.
  31. ↑ Advanced Materials, 30, 19, 5-2018, pàg. e1702057. DOI: 10.1002/adma.201702057. PMID: 28640543 [Consulta: free].
  32. ↑ PLOS ONE, 11, 7, 7-2016, pàg. e0158345. Bibcode: 2016PLoSO..1158345P. DOI: 10.1371/journal.pone.0158345. PMC: 4930208. PMID: 27367796 [Consulta: free].
  33. ↑ The International Journal of Biochemistry & Cell Biology, 84, 3-2017, pàg. 89–95. DOI: 10.1016/j.biocel.2017.01.004. PMID: 28111333 [Consulta: free].
  34. ↑ (en anglès) Optics Letters, 43, 4, 2-2018, pàg. 763–766. arXiv: 1712.00260. Bibcode: 2018OptL...43..763F. DOI: 10.1364/OL.43.000763. PMID: 29443988.
  35. ↑ Nature Communications, 11, 1, 5-2020, pàg. 2651. Bibcode: 2020NatCo..11.2651S. DOI: 10.1038/s41467-020-16437-9. PMC: 7253437. PMID: 32461637.
  36. ↑ (en anglès) Nature Communications, 7, 8-2016, pàg. 12532. Bibcode: 2016NatCo...712532Y. DOI: 10.1038/ncomms12532. PMC: 5007440. PMID: 27561914.
  37. ↑ Nature, 559, 7714, 7-2018, pàg. 343–349. arXiv: 1801.04630. Bibcode: 2018Natur.559..343J. DOI: 10.1038/s41586-018-0298-5. PMID: 30022131.
  38. ↑ Physics World, 31, 9, 26-07-2018, pàg. 5. Bibcode: 2018PhyW...31i...5W. DOI: 10.1088/2058-7058/31/9/8 [Consulta: 27 juliol 2018].
  39. ↑ Ultramicroscopy, 158, 11-2015, pàg. 98–104. DOI: 10.1016/j.ultramic.2015.07.006. PMID: 26233823 [Consulta: free].
  40. ↑ (en anglès) Nature, 543, 7645, 3-2017, pàg. 402–406. Bibcode: 2017Natur.543..402H. DOI: 10.1038/nature21698. PMID: 28300088.
  41. ↑ (en anglès) Nano Letters, 18, 2, 2-2018, pàg. 811–819. Bibcode: 2018NanoL..18..811H. DOI: 10.1021/acs.nanolett.7b04024. PMID: 29345956.
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Pticografia&oldid=34034215»