Segona forma fonamental

En geometria diferencial, la segona forma fonamental (o tensor de forma) és una forma quadràtica en el pla tangent d'una superfície suau en l'espai euclidià tridimensional, normalment denotat com $\mathrm {I\!I}$ (es llegeix "dos"). Juntament amb la primera forma fonamental, serveix per definir els invariants intrínsecs de la superfície, la seva curvatura principal. Més generalment, aquesta forma fonamental es defineix per a una subvarietat suau immersa en una varietat riemanniana.

Superfície en R³

Definició de la segona forma fonamental

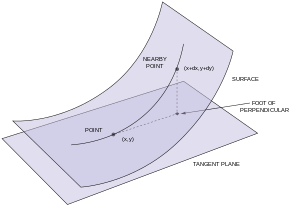
Motivació

La segona forma fonamental d'una superfície paramètrica S in R³ va ser introduïda i estudiada per Gauss. Primer, suposi's que la superfície és la gràfica d'una funció dues vegades contínuament diferenciable, z = f(x,y), i que el pla z = 0 és tangent a la superfície a l'origen. Llavors f i les seves derivades parcials respecte de x i y són zero en el punt (0,0). Per tant, l'expansió de Taylor de f en el punt (0,0) comença amb els termes quadràtics:

$z=L{\frac {x^{2}}{2}}+Mxy+N{\frac {y^{2}}{2}}+{\text{termes d'ordre major}}\,,$

i la segona forma fonamental a l'origen en les coordenades (x,y) és la forma quadràtica

$L\,dx^{2}+2M\,dx\,dy+N\,dy^{2}\,.$

Per a un punt suau P en S, es pot triar el sistema de coordenades talment que el pla z = 0 sigui tangent a S en P, i definir la segona forma fonamental de la mateixa manera.

Notació clàssica

La segona forma fonamental d'una superfície paramètrica és definida de la següent manera. Sigui r = r(u,v) una parametrització regular d'una superfície en R³, on r és una funció vectorial suau de dues variables. Se solen denotar les derivades parcials de r respecte u i v com r_u i r_v respectivament. La regularitat de la parametrització implica que r_u i r_v són linealment independents per tot (u,v) en el domini d'r, i per tant generen el pla tangent a S en cada punt. De forma equivalent, el producte escalar r_u × r_v és un vector no zero normal a la superfície. Per tant, la parametrització defineix un camp de vectors unitaris n:

$\mathbf {n} ={\frac {\mathbf {r} _{u}\times \mathbf {r} _{v}}{|\mathbf {r} _{u}\times \mathbf {r} _{v}|}}\,.$

Sovint s'escriu la segona forma fonamental com

$\mathrm {I\!I} =L\,du^{2}+2M\,du\,dv+N\,dv^{2}\,,$

la seva matriu en la base {r_u, r_v} del pla tangent és

${\begin{bmatrix}L&M\\M&N\end{bmatrix}}\,.$

Els coeficients L, M, N en un punt odnat en el pla paramètric uv són donats per les projeccions de les derivades parcials segones de r en tal punt en la línia normal a S i es poden calcular amb l'ajuda del producte escalar com:

$L=\mathbf {r} _{uu}\cdot \mathbf {n} \,,\quad M=\mathbf {r} _{uv}\cdot \mathbf {n} \,,\quad N=\mathbf {r} _{vv}\cdot \mathbf {n} \,.$

Per a un funció distància amb signe de la matriu hessiana H, es poden calcular els coeficients de la segona forma fonamental mitjançant:

$L=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{u}\,,\quad M=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,,\quad N=-\mathbf {r} _{v}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,.$

Notació en la física

En física, es defineix la segona forma fonamental d'una superfície paramètrica general S de la següent manera.

Sigui r = r(u¹,u²) una parametrització regular d'una superfície en R³, on r és una funció vectorial suau de dues variables. És habitual denotar les derivades parcials de r respecte u^α com r_α, α = 1, 2. La regularitat de la parametrització implica que r₁ i r₂ són linealment independents per tot (u¹,u²) en el domini de r, i per tant generen el pla tangent a S en cada punt. De forma equivalent, el producte vectorial r₁ × r₂ és un vector no zero normal a la superfície. Per tant, la parametrització defineix un camp de vectors unitaris n:

$\mathbf {n} ={\frac {\mathbf {r} _{1}\times \mathbf {r} _{2}}{|\mathbf {r} _{1}\times \mathbf {r} _{2}|}}\,.$

Sovint s'escriu la segona forma fonamental com

$\mathrm {I\!I} =b_{\alpha \beta }\,du^{\alpha }\,du^{\beta }\,.$

Aquesta equació utilitza el conveni de sumació d'Einstein.

Els coeficients b_αβ en un punt donat en el pla paramètric u¹u² venen donats per les projeccions de les derivades parcials segones de r en aquell punt a la línia normal a S i es poden calcular en termes del vector normal n com:

$b_{\alpha \beta }=r_{,\alpha \beta }^{\ \ \,\gamma }n_{\gamma }\,.$

Hipersuperfície en una varietat riemanniana

En l'espai euclidià, la segona forma fonamental ve donada per

$\mathrm {I\!I} (v,w)=-\langle d\nu (v),w\rangle \nu$

on $\nu$ és l'aplicació de Gauss (vector normal a la superfície), i $d\nu$ és l'aplicació progradient (pushforward) de $\nu$ tractat com una forma diferencial vectorial, i els parèntesis són el tensor mètric de l'espai euclidià.

Més generalment, en una varietat riemanniana, la segona forma fonamental és una manera equivalent de descriure l'operador de forma (denotat S) en una hipersuperfície,

$\mathrm {I} \!\mathrm {I} (v,w)=\langle S(v),w\rangle n=-\langle \nabla _{v}n,w\rangle n=\langle n,\nabla _{v}w\rangle n\,,$

on ∇_vw denota la derivada covariant de la varietat ambient i n un cos de vectors normals en la hipsersuperfície. (Si la connexió afí no té torsió, llavors la segona forma fonamental és simètrica.)

El signe de la segona forma fonamental depèn de la tria de la direcció de n (que s'anomena la co-orientació de la hipersuperfície - per a superfícies en l'espai euclidià, ve donada de forma equivalent per la tria de l'orientabilitat de la superfície).

Generalització a codimensió arbitrària

Es pot generalitzar la segona forma fonamental a codimensió arbitrària. En tal cas, es tracta d'una forma quadràtica en l'espai tangencial amb valors en el fibrat normal i es pot definir com

$\mathrm {I\!I} (v,w)=(\nabla _{v}w)^{\bot }\,,$

on $(\nabla _{v}w)^{\bot }$ denota la projecció ortogonal de la derivada covariant $\nabla _{v}w$ en el fibrat normal.

En l'espai euclidià, es pot descriure el tensor de curvatura d'una subvarietat amb la següent fórmula:

$\langle R(u,v)w,z\rangle =\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle .$

Aquesta expressió rep el nom d'equació de Gauss–Codazzi, ja que es pot veure com una generalització del teorema egregi de Gauss.

Per varietat riemannianes generals, s'ha de sumar la curvatura de l'espai ambient; si N és una varietat immersa en una varietat riemanniana (M,g) llavors es pot expressar el tensor de curvatura R_N de N amb la mètrica induïda utilitzant la segona forma fonamental i R_M, el tensor de cuvatura de M:

$\langle R_{N}(u,v)w,z\rangle =\langle R_{M}(u,v)w,z\rangle +\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle \,.$

Vegeu també

• Primera forma fonamental
• Curvatura gaussiana
• Tercera forma fonamental
• U-forma canònica

Bibliografia

• Guggenheimer, Heinrich. «Chapter 10. Surfaces». A: Differential Geometry. Dover, 1977. ISBN 0-486-63433-7. 
• Kobayashi, Shoshichi. Foundations of Differential Geometry, Vol. 2. New. Wiley-Interscience, 1996. ISBN 0-471-15732-5. 
• Spivak, Michael. A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish, 1999. ISBN 0-914098-72-1. 

Enllaços externs

• Steven Verpoort (2008) Geometry of the Second Fundamental Form: Curvature Properties and Variational Aspects from Katholieke Universiteit Leuven.