Tessel·lació regular
 Una tessel·lació regular té només un tipus de polígon regular |
 Una tessel·lació semirregular o uniforme té un tipus de vèrtex, però dos o més tipus de polígons regulars |
 Una tessel·lació k- uniforme té k tipus de vèrtexs i dos o més tipus de polígons regulars |
 Una tessel·lació que no és aresta amb aresta pot tenir polígons regulars de diferents mides |
Una tessel·lació regular o tessel·lació amb polígons regulars és un tesel·lació del pla que empra un sol tipus de polígons regulars.[1] Aquests patrons geomètrics han estat àmpliament utilitzats amb fins decoratius des de l'antiguitat. Només són possibles tesel·lacions regulars emprant triangles equilàters, quadrats i hexàgons regulars.
El primer tractament matemàtic sistemàtic del tema va ser el de Kepler en el seu llibre Harmonices Mundi (llatí: L’harmonia del món, 1619).
Tessel·lació regular o perfecta
[modifica]Segons Grünbaum i Shephard (secció 1.3), es diu que una tessel·lació és regular o perfecta si el grup de simetria del tessel·lat opera transitivament sobre els elements de la tessel·lació, on un element consisteix d'un vèrtex mútuament incident, una aresta i una tessel·la. Això vol dir que per cada parell d'elements hi ha una operació de simetria que els associa entre si.
Això és equivalent a una tesel·lació aresta amb aresta (aresta compartida) de polígons regulars congruents. Hi ha d'haver sis triangles equilàters, quatre quadrats o tres hexàgons regulars en cada vèrtex, produint les tres tessel·lacions regulars.
| p6m, *632 | p4m, *442 | |
|---|---|---|
 
|
 
|
 
|
 3⁶ (t=1, e=1) |
 63 (t=1, e=1) |
 44 (t=1, e=1) |
Tessel·lació semiregular, uniforme o d'Arquimedes
[modifica]La transitivitat de vèrtex vol dir que per cada parell de vèrtexs hi ha una operació de simetria que associa el primer vèrtex amb el segon.[2]
Si el requisit de la transitivitat d'element es relaxa a transitivitat de vèrtex, mentre que es manté la condició de la teselación aresta amb aresta, apareixen 8 teselacions addicionals possibles, conegudes com tessel·lacions semiregulars, tessel·lacions uniformes o tessel·lacions d'Arquimedes. Cal tenir en compte que hi ha dues formes especulars (enantiomorfes o quirals) de la tessel·lació 34.6 (hexagonal rom), les quals es mostren en la següent taula. Totes les altres tessel·lacions regulars i semiregulars són aquirals.
| p6m, *632 | |||||
|---|---|---|---|---|---|
   3.12² (t=2, e=2) t{6,3} |
   3.4.6.4 (t=3, e=2) rr{3,6} |
   4.6.12 (t=3, e=3) tr{3,6} |
   (3.6)² (t=2, e=1) r{6,3} | ||
   4.8² (t=2, e=2) t{4,4} |
   3².4.3.4 (t=2, e=2) s{4,4} |
   33.4² (t=2, e=3) {3,6}:e |
   34.6 (t=3, e=3) sr{3,6} | ||
Grünbaum i Shephard distingeixen la descripció d'aquestes tessel·lalcions com d'Arquimedes referint únicament a la propietat local que la disposició de les tessel·les al voltant de cada vèrtex és la mateixa, i el terme uniforme es refereix a la propietat global de la transitivitat de vèrtex. Encara que aquests produeixen el mateix conjunt de tessel·lats en el pla, en altres espais hi tessel·lats d'Arquimedes que no són uniformes.
Altres exemples de tessel·lació semiregular són:
-
3.7.42
-
3.8.24
-
3.9.18
-
3.10.15
-
4.5.20
-
5.5.10
-
6.6.6
-
3.3.4.12
-
3.4.3.12
-
3.3.6.6
-
4.4.4.4
-
3.4.4.6
Tessel·lació k-uniforme o k-isogonal
[modifica] per arestes, triangles grocs, quadrats vermells (per polígons) |
 per posicions 4-isoèdriques, 3 colors per ombrejar els triangles (per òrbites) |
Aquestes tessel·lacions periòdiques es poden classificar pel nombre d'òrbites de vèrtexs, arestes i tessel·les. Si hi ha k òrbites de vèrtexs, una tessel·lació es coneix com k-uniforme o k-isogonal; si hi ha t òrbites de tessel·les, com t-isoèdric; si hi ha e òrbites d'arestes, com e-isotoxal.
La tessel·lació k-uniforme amb les mateixes figures de vèrtex es poden identificar encara més per la seva simetria de grups de paper pintat.
La tessel·lació 1-uniforme inclouen 3 tessel·lacions regulars i 8 tessel·lacions semirregulars, amb dos o més tipus de polígons regulars. Hi ha 20 tessel·lacions 2-uniforme, 61 tessel·lacions 3-uniformes, 151 tessel·lacions 4-uniformes, 332 tessel·lacions 5-uniformes i 673 tessel·lacions 6-uniformes. Cadascuna es pot agrupar pel nombre m de figures de vèrtex diferents, que també s’anomenen tessel·lacions m- arquimedianes.[3]
Finalment, si el nombre de tipus de vèrtexs és el mateix que la uniformitat (m = k), es diu que la tessel·lació és Krotenheerdt. En general, la uniformitat és superior o igual al nombre de tipus de vèrtexs (m ≥ k), ja que els diferents tipus de vèrtexs necessàriament tenen òrbites diferents, però no al revés. Configurant m = n = k, hi ha 11 tessel·lacions d’aquest tipus per a n = 1; 20 tessel·lacions d'aquest tipus per a n = 2; 39 tessel·lacions per a n = 3; 33 tessel·lacions per a n = 4; 15 tessel·lacions per a n = 5; 10 tessel·lacions per a n = 6; i 7 tessel·lacions per a n = 7.
| m-arquimediana | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ≥ 15 | Total | ||
| k-uniforme | 1 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 2 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | |
| 3 | 0 | 22 | 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 61 | |
| 4 | 0 | 33 | 85 | 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 151 | |
| 5 | 0 | 74 | 149 | 94 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 332 | |
| 6 | 0 | 100 | 284 | 187 | 92 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 673 | |
| 7 | 0 | ? | ? | ? | ? | ? | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 8 | 0 | ? | ? | ? | ? | ? | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 9 | 0 | ? | ? | ? | ? | ? | ? | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 10 | 0 | ? | ? | ? | ? | ? | ? | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 11 | 0 | ? | ? | ? | ? | ? | ? | ? | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 12 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | 0 | 0 | 0 | 0 | 0 | ? | |
| 13 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | 0 | 0 | ? | |
| 14 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | 0 | ? | |
| ≥ 15 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ? | |
| Total | 11 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | ∞ | |
Polígons regulars disseccionats
[modifica]Algunes tessel·lacions k-uniformes es poden derivar mitjançant la dissecció simètrica dels polígons de la tessel·lació amb arestes interiors, per exemple (dissecció directa):
 |
 |
 |
| Hexàgon | Dodecàgon (cadascun té dues orientacions) | |
|---|---|---|
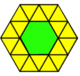
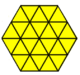
Algunes tessel·lacions k-uniformes es poden derivar mitjançant la dissecció de polígons regulars amb nous vèrtexs al llarg de les vores originals, per exemple (dissecció indirecta):

|

|

|

|

|

|
|
|
| Triangle | Quadrat | Hexàgon | |||||
|---|---|---|---|---|---|---|---|
Finalment, per veure molts tipus de configuracions de vèrtexs (vegeu planígon).
Tessel·lació 2-uniforme
[modifica]Hi ha 20 tessel·lacions 2-uniforme del pla euclidià (també anomenats tessel·lacions 2-isogonals o tessel·lacions demiregulars),[5][6][7] S'enumeren els tipus de vèrtex per a cadascuna. Si dues tessel·lacions comparteixen els mateixos dos tipus de vèrtex, se les afegeix els subíndex 1 o 2.
| p6m, *632 | p4m, *442 | |||||
|---|---|---|---|---|---|---|
 [3⁶; 3².4.3.4] (t=3, e=3) |
 [3.4.6.4; 3².4.3.4] (t=4, e=4) |
 [3.4.6.4; 33.4²] (t=4, e=4) |
 [3.4.6.4; 3.4².6] (t=5, e=5) |
 [4.6.12; 3.4.6.4] (t=4, e=4) |
 [3⁶; 3².4.12] (t=4, e=4) |
 [3.12.12; 3.4.3.12] (t=3, e=3) |
| p6m, *632 | p6, 632 | p6, 632 | cmm, 2*22 | pmm, *2222 | cmm, 2*22 | pmm, *2222 |
 [3⁶; 3².6]² (t=2, e=3) |
 [3⁶; 34.6]1 (t=3, e=3) |
 [3⁶; 34.6]₂ (t=5, e=7) |
 [3².6²; 34.6] (t=2, e=4) |
 [3.6.3.6; 3².6²] (t=2, e=3) |
 [3.4².6; 3.6.3.6]₂ (t=3, e=4) |
 [3.4².6; 3.6.3.6]1 (t=4, e=4) |
| p4g, 4*2 | pgg, 22× | cmm, 2*22 | cmm, 2*22 | pmm, *2222 | cmm, 2*22 | |
 [33.4²; 3².4.3.4]1 (t=4, e=5) |
 [33.4²; 3².4.3.4]₂ (t=3, e=6) |
 [44; 33.4²]1 (t=2, e=4) |
 [44; 33.4²]₂ (t=3, e=5) |
 [3⁶; 33.4²]1 (t=3, e=4) |
 [3⁶; 33.4²]₂ (t=4, e=5) | |
Tessel·lacions k-uniforme superiors
[modifica]S'han enumerat fins a k=6 tessel·lacions k-uniforme. Hi ha 673 tessel·lacions 6-uniforme del pla euclidià. La cerca de Brian Galebach va reproduir la llista de 10 tessel·lacions 6-uniforme de Krotenheerdt amb 6 tipus de vèrtex diferents, a més de trobar 92 d'elles amb 5 tipus de vèrtex, 187 d'elles amb 4 tipus de vèrtex, 284 d'elles amb 3 tipus de vèrtex i 100 amb 2 tipus de vèrtex.
Fractalització de tessel·lacions k-uniforme
[modifica]Hi ha moltes maneres de generar noves tessel·lacions k-uniforme a partir de les anteriors tessel·lacions k-uniforme. Per exemple, es pot observar que la tessel·lació 2-uniforme [3.12.12; 3.4.3.12] forma una xarxa quadrada, la tessel·lació 4(3-1)-uniforme [343.12; (3.12²)3] forma una xarxa quadrada xata, i la tessel·lació 5(3-1-1)-uniforme [334.12; 343.12; (3.12.12)3] forma una xarxa triangular allargada. Aquests tessel·lacions uniformes d’ordre superior utilitzen el mateix entramat però tenen una major complexitat.
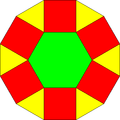
La base de la fractalització d’aquestes tessel·lacions és la següent:[8]
| Triangle | Quadrat | Hexàgon | Dodecàgon
disseccionat | |
|---|---|---|---|---|
| Figura |  |
 |
 |
 |
| Fractalització |  |
 |
 |
 |
Les longituds laterals es dilaten amb un factor de .
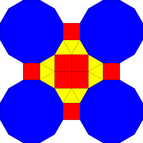
Això es pot fer de manera similar amb la tessel·lació trihexagonal truncada com a base, amb la corresponent dilatació de .
| Triangle | Quadrat | Hexàgon | Dodecàgon
disseccionat | |
|---|---|---|---|---|
| Figura |  |
 |
 |
 |
| Fractalizació |  |
 |
 |
 |
Exemples de fractalització
[modifica]| Tessel·lació hexagonal truncada | Tessel·lació trihexagonal truncada | |
|---|---|---|
| Fractalització |  |
 |
Tessel·lació que no és aresta amb aresta
[modifica]
Els polígons regulars convexos també poden formar tessel·lacions planes que no siguin d'aresta amb aresta. Aquests tessel·lacions es poden considerar d'aresta amb aresta de polígons no regulars amb arestes colineals adjacents.
Hi ha set famílies d'isogonals, cada família té un paràmetre de valor real que determina la superposició entre els costats de les tessel·les adjacents o la proporció entre les longituds de l'aresta de les tessel·les diferents. Es generen dues de les famílies a partir de posicions quadrades desplaçades, ja sigui progressives o en ziga-zaga. Grünbaum i Shephard anomenen aquestes tessel·lacions uniformes, tot i que contradiu la definició de Coxeter d’uniformitat que requereix polígons regulars d'aresta amb aresta. Aquestes tessel·lacions isogonals són en realitat topològicament idèntiques a les tessel·lacions uniformes, amb diferents proporcions geomètriques.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
 Fileres de quadrats amb desplaçaments horitzontals |
 Fileres de triangles amb desplaçaments horitzontals |
 Una tessel·lació per quadrats (tessel·lació pitagòrica) |
 Tres hexàgons que envolten cada triangle |
 Sis triangles que envolten cada hexàgon |
 Tres triangles que envolten un triangle | |
| cmm (2*22) | p2 (2222) | cmm (2*22) | p4m (*442) | p6 (632) | p3 (333) | |
Tessel·lació uniforme en el pla hiperbòlic
[modifica]Aquests tessel·lats estan també relacionats amb els políedres regulars i semiregulars i els tessel·lats del pla hiperbòlic. Els políedres semiregulars es fan a partir de cares que són polígons regulars, però els seus angles en un punt sumen menys de 360 graus. Els polígons regulars en la geometria hiperbòlica tenen angles més petits que el que posseeixen en el pla. En ambdós casos, que la disposició de polígons sigui la mateixa a cada vèrtex, no vol dir que el poliedre o la tessel·lació sigui vèrtex-transitiu.
Alguns tessel·lat regulars del pla hiperbòlic (usant la projecció del model de disc de Poincaré) són:
Referències
[modifica]- ↑ «9.3 Teselaciones regulares y semiregulares». A: Matemáticas. Profesores de Enseñanza Secundaria (en castellà). II. MAD-Eduforma, 2003, p. 361. ISBN 84-665-1263-2-X.
- ↑ Critchlow, 1970, p. 60-61.
- ↑ Lenngren, 2009.
- ↑ Galebach, Brian. «n-uniform tilings» (en anglès). Probability sports.
- ↑ Critchlow, 1970, p. 62-67.
- ↑ Grünbaum i Shephard, 1986, p. 65-67.
- ↑ «In Search of Demiregular Tilings» (
 PDF) (en anglès). Arxivat de l'original el 2016-05-07. [Consulta: 7 febrer 2021].
PDF) (en anglès). Arxivat de l'original el 2016-05-07. [Consulta: 7 febrer 2021].
- ↑ Chavey, 2014, p. 193-210.
- ↑ Nelsen, Roger B «Paintings, plane tilings, and proofs» (
 PDF) (en anglès). Math Horizons, 11(2), 11-2003, pàg. 5–8. DOI: 10.1080/10724117.2003.12021741.. Reimprès en Haunsperger, Deanna; Kennedy, Stephen «The Edge of the Universe: Celebrating Ten Years of Math Horizons» (en anglès). Mathematical Association of America, 2007, pàg. 295–298.
PDF) (en anglès). Math Horizons, 11(2), 11-2003, pàg. 5–8. DOI: 10.1080/10724117.2003.12021741.. Reimprès en Haunsperger, Deanna; Kennedy, Stephen «The Edge of the Universe: Celebrating Ten Years of Math Horizons» (en anglès). Mathematical Association of America, 2007, pàg. 295–298.
Bibliografia
[modifica]- Chavey, D «Tilings by Regular Polygons - II: A Catalog of Tilings» (en anglès). Computers & Mathematics with Applications, 1989, pàg. vol. 17, 147-165. DOI: 10.1016/0898-1221(89)90156-9.
- Chavey, Darrah «Tilling by regular polygons III: Dodecagon-dense tillings» (en anglès). Symmetry-Culture and Science, 25(3), 2014.
- Critchlow, Keith. Order in Space: A design source book (en anglès), 1970. ISBN 978-0-670-52830-1.
- Debroey, I; Landuyt, F «Equitransitive edge-to-edge tilings» (en anglès). Geometriae Dedicata, 11(1), 1981, pàg. 47–60. DOI: 10.1007/BF00183189.
- Ding, Ren; Reay, John R «The boundary characteristic and Pick's theorem in the Archimedean planar tilings» (en anglès). J. Combinat. Theory A, 44(1), 1987, pàg. 110–119. DOI: 10.1016/0097-3165(87)90063-X.
- Dutch, Steve. «Uniform Tilings» (en anglès). University of Wisconsin - Green Bay. Arxivat de l'original el 2006-09-09. [Consulta: 7 febrer 2021].
- Grünbaum, Branko; Shephard, Geoffrey C «Tilings by regular polygons» (en anglès). Math. Mag., 50(5), 1977, pàg. 227–247. DOI: 10.2307/2689529. JSTOR: 2689529.
- Grünbaum, Branko; Shephard, Geoffrey C «The ninety-one types of isogonal tilings in the plane» (en anglès). Trans. Am. Math. Soc., 252, 1978, pàg. 335–353. DOI: 10.1090/S0002-9947-1978-0496813-3.
- Grünbaum, Branko; Shephard, Geoffrey C. Tilings and Patterns (en anglès). W. H. Freeman and Company, 1987. ISBN 0-7167-1193-1.
- Kovic, Jurij «Symmetry-type graphs of Platonic and Archimedean solids» (en anglès). Math. Commun., 16(2), 2011, pàg. 491–507.
- Lenngren, Nils «k-uniform tilings by regular polygons» (
 PDF) (en anglès). Uppsala Universitet (Department of Mathematics), 2009. Arxivat de l'original el 2015-06-30 [Consulta: 7 febrer 2021].
PDF) (en anglès). Uppsala Universitet (Department of Mathematics), 2009. Arxivat de l'original el 2015-06-30 [Consulta: 7 febrer 2021]. - Mitchell, K. «Semi-Regular Tilings» (en anglès). Hobart and William Smith Collleges.
- Pellicer, Daniel; Williams, Gordon «Minimal Covers of the Archimedean Tilings, Part 1» (en anglès). The Electronic Journal of Combinatorics, 19(3), 2012, pàg. #P6. DOI: 10.37236/2512.
- Préa, P «Distance sequences and percolation thresholds in Archimedean Tilings» (en anglès). Mathl. Comput. Modelling, 26(8)-26(10), 1997, pàg. 317–320. DOI: 10.1016/S0895-7177(97)00216-1.
- Seymour, Dale; Britton, Jill. Introduction to Tessellations (en anglès), 1989, p. 50–57. ISBN 978-0866514613.
- Sommerville, Duncan MacLaren Young. «cap. X: The Regular Polytopes». A: An Introduction to the Geometry of n Dimensions (en anglès). Dover Publications, 1958.
Vegeu també
[modifica]- Geometria hiperbòlica
- Políedres regulars (els sòlids platònics)
- Poliedres semiregulars (inclosos els Políedres arquimedians)
- Símbol de Wythoff
- Tessel·lació amb rectangles
- Tessel·lació aperiòdica
- Tessel·lació de Penrose
Enllaços externs
[modifica]- Weisstein, Eric W., «Tessellation» a MathWorld (en anglès).
- Weisstein, Eric W., «Semiregular tessellation» a MathWorld (en anglès).
- Weisstein, Eric W., «Demiregular tessellation» a MathWorld (en anglès).
























