Usuari:Jaumellecha/proves3

En física i matemàtiques, una corba braquistòcrona (del grec βράχιστος χρόνος (brákhistos khrónos); «temps més curt»), o «corba de descens més ràpid», és la que es troba en el pla entre un punt A i un punt inferior B, on B no és directament sota A, sobre la qual una bola llisca sense fricció sota la influència d'un camp gravitatori uniforme fins a un punt final determinat en el temps més curt. El problema va ser plantejat per Johann Bernoulli el 1696.

• 
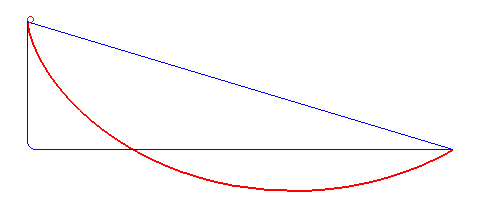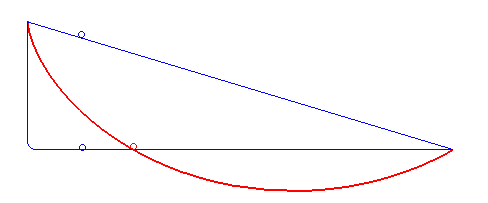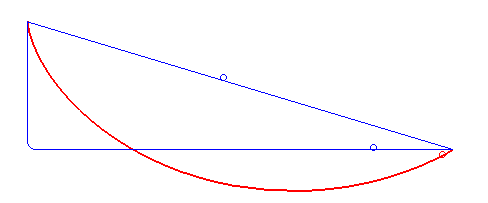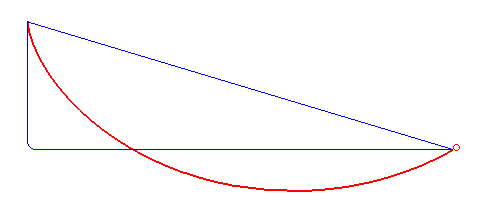
  La corba de descens més ràpid no és una línia recta o poligonal (blava) sinó una cicloide (vermell)

La corba braquistòcrona té la mateixa forma que la corba tautòcrona; tots dos són cicloides. Tanmateix, la porció de la cicloide utilitzada per a cadascun dels dos varia. Més concretament, la braquistòcrona pot utilitzar fins a una rotació completa de la cicloide (al límit quan A i B estan al mateix nivell), però sempre comença en una cúspide. En canvi, el problema tautòcrona només pot utilitzar fins a la primera meitat de rotació, i sempre acaba a l'horitzontal. El problema es pot resoldre mitjançant eines del càlcul de variacions i control òptim.

La corba és independent tant de la massa del cos de prova com de la força de gravetat local. Només s'escull un paràmetre perquè la corba s'ajusti al punt inicial A i al punt final B. Si al cos se li dóna una velocitat inicial en A, o si es té en compte la fricció, aleshores la corba que minimitza el temps difereix de la corba tautòcrona.

Història

Johann Bernoulli va plantejar el problema de la braquistòcrona als lectors d'Acta Eruditorum el juny de 1696.

Va dir:

«	Jo, Johann Bernoulli, em dirigeixo als matemàtics més brillants del món. Res és més atractiu per a les persones intel·ligents que un problema honest i desafiant, la possible solució del qual atorgarà fama i es mantindrà com un monument durador. Seguint l'exemple donat per Pascal, Fermat, etc., espero obtenir l'agraïment de tota la comunitat científica posant davant els millors matemàtics del nostre temps un problema que posarà a prova els seus mètodes i la força del seu intel·lecte. Si algú em comunica la solució del problema proposat, el declararé públicament digne de lloança.	»
— Johann Bernoulli

Bernoulli va escriure l'enunciat del problema de la següent manera:

«

Donats dos punts A i B en un pla vertical, quina és la corba traçada per un punt sobre el qual només actua la gravetat, que comença a A i arriba a B en el menor temps?

»

Johann i el seu germà Jakob Bernoulli van derivar la mateixa solució, però la derivació de Johann era incorrecta, i va intentar fer passar la solució de Jakob com la seva. Johann va publicar la solució a la revista el maig de l'any següent i va assenyalar que la solució és la mateixa corba que la corba tautòcrona de Huygens. Després de derivar l'equació diferencial per a la corba pel mètode que es mostra a continuació, va continuar demostrant que produeix un cicloide. Tanmateix, la seva prova es veu afectada per l'ús d'una sola constant en lloc de les tres constants, v_m, 2g i D, a continuació.

Bernoulli va permetre sis mesos per a les solucions, però no es va rebre cap durant aquest període. A petició de Leibniz, el temps es va prorrogar públicament durant un any i mig. A les 16.00 h. del 29 de gener de 1697, quan va arribar a casa des de la Royal Mint, Isaac Newton va trobar el repte en una carta de Johann Bernoulli. Newton es va quedar despert tota la nit per resoldre'l i va enviar la solució de forma anònima al següent missatge. En llegir la solució, Bernoulli va reconèixer immediatament el seu autor, exclamant que «reconec un lleó per la seva marca de les urpes». Aquesta història dóna una idea del poder de Newton, ja que Johann Bernoulli va trigar dues setmanes a resoldre'l. Newton també va escriure: «No m'encanta que els estrangers em burlin de coses matemàtiques...», i Newton ja havia resolt el problema de resistència mínima de Newton, que es considera el primer d'aquest tipus en càlcul de variacions.

Al final, cinc matemàtics van respondre amb solucions: Isaac Newton, Jakob Bernoulli, Gottfried Leibniz, Ehrenfried Walther von Tschirnhaus i Guillaume de l'Hôpital. Quatre de les solucions (excloent la de l'Hôpital) es van publicar a la mateixa edició de la revista que la de Johann Bernoulli. En el seu article, Jakob Bernoulli va donar una prova de la condició durant menys temps similar a la següent abans de demostrar que la seva solució és una cicloide. Segons l'estudiós newtonià Tom Whiteside, en un intent de superar al seu germà, Jakob Bernoulli va crear una versió més difícil del problema de la braquistòcrona. Per resoldre-ho, va desenvolupar nous mètodes que van ser refinats per Leonhard Euler en el que aquest últim va anomenar (el 1766) el càlcul de variacions. Joseph-Louis Lagrange va fer més treballs que van donar lloc al càlcul infinitesimal modern.

Abans, l'any 1638, Galileu havia intentat resoldre un problema similar per al camí del descens més ràpid d'un punt a una paret a les seves Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze. Treu la conclusió que l'arc de cercle és més ràpid que qualsevol nombre de les seves cordes:

«

De l'anterior es pot inferir que el camí més ràpid de tots [lationem omnium velocissimam], d'un punt a un altre, no és el camí més curt, és a dir, una recta, sinó l'arc del cercle. (...) En conseqüència, com més s'acosta el polígon inscrit a una circumferència, més curt és el temps necessari per baixar d'A a C. El que s'ha demostrat per al quadrant és cert també per als arcs més petits; el raonament és el mateix.

»

Just després del Teorema 6 de Due Nuove Scienze, Galileu adverteix de possibles fal·làcies i de la necessitat d'una «ciència superior». En aquest diàleg Galileu repassa la seva pròpia obra. Galileu va estudiar la cicloide i li va donar nom, però la connexió entre aquesta i el seu problema va haver d'esperar als avenços de les matemàtiques.

• 
  Diagrames sobre la conjectura de Galileu

La conjectura de Galileu és que «El temps més curt de tots [per a un cos mòbil] serà el de la seva caiguda al llarg de l'arc ADB [d'un quart de cercle] i propietats similars s'han d'entendre com una retenció per a tots els arcs menors agafats cap amunt des del límit més baix B».

En conseqüència, a la figura 1, del Diàleg sobre els dos sistemes mundials principals, Galileu afirma que el cos lliscant al llarg de l'arc circular d'un quart de cercle, d'A a B, arribarà a B en menys temps que si prengués qualsevol altre camí d'A a B. De la mateixa manera, a la figura 2, des de qualsevol punt E de l'arc AB, afirma que el temps al llarg de l'arc menor EB serà menor que per a qualsevol altre camí d'E a B. De fet, el camí més ràpid d'A a B o d'E a B, la braquistòcrona, és un arc cicloïdal, que es mostra a la figura 3 per al camí d'E a B. Les dues corbes es superposen a la figura 4. Nota: la conjectura de Galileu té la tangent de la corba horitzontal al punt final, B, mentre que la braquistòcrona té la tangent vertical al punt inicial, E. Com a conseqüència, l'arc circular i l'arc cicloïdal de la figura 4 s'han de tallar en algun punt entre E i B.

La solució de Johann Bernoulli

Introducció

En una carta a L'Hôpital, (21/12/1696), Bernoulli va afirmar que quan es plantejava el problema de la corba de descens més ràpid, després de només dos dies va notar una curiosa afinitat o connexió amb un altre problema no menys notable que portava a un «mètode indirecte» de solució. Poc després va descobrir un «mètode directe».

El mètode directe

En una carta a Henri Basnage, conservada a la Biblioteca Pública de la Universitat de Basilea, datada el 30 de març de 1697, Johann Bernoulli va declarar que havia trobat dos mètodes (sempre anomenats «directe» i «indirecte») per demostrar que la braquistòcrona era la «cicloide comuna», també anomenada «ruleta». Seguint el consell de Leibniz, va incloure només el «mètode indirecte» a l'Acta Eruditorum Lipsidae de maig de 1697. Va escriure que això era en part perquè creia que era suficient per convèncer qualsevol que dubtés de la conclusió, en part perquè també va resoldre dos famosos problemes d'òptica que «el difunt senyor Huygens» havia plantejat en el seu tractat de la llum. En la mateixa carta va criticar a Newton per amagar el seu mètode.

A més del seu mètode indirecte, també va publicar les altres cinc respostes al problema que va rebre.

El «mètode directe» de Johann Bernoulli és històricament important com a prova que la braquistòcrona és el cicloide. El mètode consisteix a determinar la curvatura de la corba en cada punt. Totes les altres proves, inclosa la de Newton (que no es va revelar en aquell moment) es basen en trobar el gradient en cada punt.

El 1718, Bernoulli va explicar com va resoldre el problema de la braquistòcrona pel seu mètode directe.

Va explicar que no l'havia publicat el 1697, per raons que ja no s'aplicaven el 1718. Aquest article va ser ignorat en gran mesura fins al 1904, quan Constantin Carathéodory va apreciar per primera vegada la profunditat del mètode, que va afirmar que demostra que la cicloide és el única corba possible de baixada més ràpida. Segons ell, les altres solucions simplement implicaven que el temps de descens és estacionari per a la cicloide, però no necessàriament el mínim possible.

La solució analítica

Brachistochrone Bernoulli Direct Method

46- A body is regarded as sliding along any small circular arc Ce between the radii KC and Ke, with centre K fixed. The first stage of the proof involves finding the particular circular arc, Mm, which the body traverses in the minimum time.

45- The line KNC intersects AL at N, and line Kne intersects it at n, and they make a small angle CKe at K. Let NK = a, and define a variable point, C on KN extended. Of all the possible circular arcs Ce, it is required to find the arc Mm, which requires the minimum time to slide between the 2 radii, KM and Km. To find Mm Bernoulli argues as follows.

44- Let MN = x. He defines m so that MD = mx, and n so that Mm = nx + na and notes that x is the only variable and that m is finite and n is infinitely small. The small time to travel along arc Mm is ${\frac {Mm}{MD^{\frac {1}{2}}}}={\frac {n(x+a)}{(mx)^{\frac {1}{2}}}}$, which has to be a minimum (‘un plus petit’). He does not explain that because Mm is so small the speed along it can be assumed to be the speed at M, which is as the square root of MD, the vertical distance of M below the horizontal line AL.

It follows that, when differentiated this must give

${\frac {(x-a)dx}{2x^{\frac {3}{2}}}}=0$ so that x = a.

43- This condition defines the curve that the body slides along in the shortest time possible. For each point, M on the curve, the radius of curvature, MK is cut in 2 equal parts by its axis AL. This property, which Bernoulli says had been known for a long time, is unique to the cycloid.

42- Finally, he considers the more general case where the speed is an arbitrary function X(x), so the time to be minimised is ${\frac {(x+a)}{X}}$. The minimum condition then becomes

$X={\frac {(x+a)dX}{dx}}$

which he writes as :$X=(x+a)\Delta x$ 41- and which gives MN (=x) as a function of NK (= a). From this the equation of the curve could be obtained from the integral calculus, though he does not demonstrate this.

La solució sintètica

40- He then proceeds with what he called his Synthetic Solution, which was a classical, geometrical proof, that there is only a single curve that a body can slide down in the minimum time, and that curve is the cycloid.

39- The reason for the synthetic demonstration, in the manner of the ancients, is to convince Mr de la Hire. He has little time for our new analysis, describing it as false (He claims he has found 3 ways to prove that the curve is a cubic parabola) – Letter from Johan Bernoulli to Pierre Varignon dated 27 Jul 1697.

38- Assume AMmB is the part of the cycloid joining A to B, which the body slides down in the minimum time. Let ICcJ be part of a different curve joining A to B, which can be closer to AL than AMmB. If the arc Mm subtends the angle MKm at its centre of curvature, K, let the arc on IJ that subtends the same angle be Cc. The circular arc through C with centre K is Ce. Point D on AL is vertically above M. Join K to D and point H is where CG intersects KD, extended if necessary.

Let $\tau$ and t be the times the body takes to fall along Mm and Ce respectively.

$\tau \propto {\frac {Mm}{MD^{\frac {1}{2}}}}$, $t\propto {\frac {Ce}{CG^{\frac {1}{2}}}}$,

Extend CG to point F where, $CF={\frac {CH^{2}}{MD}}$ and since ${\frac {Mm}{Ce}}={\frac {MD}{CH}}$, it follows that

${\frac {\tau }{t}}={\frac {Mm}{Ce}}.\left({\frac {CG}{MD}}\right)^{\frac {1}{2}}=\left({\frac {CG}{CF}}\right)^{\frac {1}{2}}$

Since MN = NK, for the cycloid:

$GH={\frac {MD.HD}{DK}}={\frac {MD.CM}{MK}}$, $CH={\frac {MD.CK}{MK}}={\frac {MD.(MK+CM)}{MK}}$, and $CG=CH+GH={\frac {MD.(MK+2CM)}{MK}}$

If Ce is closer to K than Mm then

$CH={\frac {MD.(MK-CM)}{MK}}$ and $CG=CH-GH={\frac {MD.(MK-2CM)}{MK}}$

In either case,

$CF={\frac {CH^{2}}{MD}}>CG$, and it follows that $\tau <t$

37- If the arc, Cc subtended by the angle infinitesimal angle MKm on IJ is not circular, it must be greater than Ce, since Cec becomes a right-triangle in the limit as angle MKm approaches zero.

36- Note, Bernoulli proves that CF > CG by a similar but different argument.

35- From this he concludes that a body traverses the cycloid AMB in less time than any other curve ACB.

Mètode indirecte

34- According to Fermat’s principle, the actual path between two points taken by a beam of light is one that takes the least time. In 1697 Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).

33- By the conservation of energy, the instantaneous speed of a body v after falling a height y in a uniform gravitational field is given by:

$v={\sqrt {2gy}}$,

32- The speed of motion of the body along an arbitrary curve does not depend on the horizontal displacement.

31- Bernoulli noted that the law of refraction gives a constant of the motion for a beam of light in a medium of variable density:

${\frac {\sin {\theta }}{v}}={\frac {1}{v}}{\frac {dx}{ds}}={\frac {1}{v_{m}}}$,

30- where v_m is the constant and $\theta$ represents the angle of the trajectory with respect to the vertical.

29- The equations above lead to two conclusions: 28- # At the onset, the angle must be zero when the particle speed is zero. Hence, the brachistochrone curve is tangent to the vertical at the origin. 27- # The speed reaches a maximum value when the trajectory becomes horizontal and the angle θ = 90°.

26- Assuming for simplicity that the particle (or the beam) with coordinates (x,y) departs from the point (0,0) and reaches maximum speed after falling a vertical distance D:

$v_{m}={\sqrt {2gD}}$.

Rearranging terms in the law of refraction and squaring gives:

$v_{m}^{2}dx^{2}=v^{2}ds^{2}=v^{2}(dx^{2}+dy^{2})$

which can be solved for dx in terms of dy:

$dx={\frac {v\,dy}{\sqrt {v_{m}^{2}-v^{2}}}}$.

Substituting from the expressions for v and v_m above gives:

$dx={\sqrt {\frac {y}{D-y}}}\,dy\,,$

25- which is the differential equation of an inverted cycloid generated by a circle of diameter D=2r, whose parametric equation is:

${\begin{aligned}x&=r(\varphi -\sin \varphi )\\y&=r(1-\cos \varphi ).\end{aligned}}$

24- where φ is a real parameter, corresponding to the angle through which the rolling circle has rotated. For given φ, the circle's centre lies at (x, y) = (rφ, r).

23- In the brachistochrone problem, the motion of the body is given by the time evolution of the parameter:

$\varphi (t)=\omega t\,,\omega ={\sqrt {\frac {g}{r}}}$

where t is the time since the release of the body from the point (0,0).

La solució de Jakob Bernoulli

22- Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time, then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,

$ds^{2}=dx^{2}+dy^{2}$.

On differentiation with dy fixed we get,

$2ds\ d^{2}s=2dx\ d^{2}x$.

And finally rearranging terms gives,

${\frac {dx}{ds}}d^{2}x=d^{2}s=v\ d^{2}t$

21- where the last part is the displacement for given change in time for 2nd differentials. Now consider the changes along the two neighboring paths in the figure below for which the horizontal separation between paths along the central line is d²x (the same for both the upper and lower differential triangles). Along the old and new paths, the parts that differ are,

Path function

$d^{2}t_{1}={\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}d^{2}x$

$d^{2}t_{2}={\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}d^{2}x$

For the path of least times these times are equal so for their difference we get,

$d^{2}t_{2}-d^{2}t_{1}=0={\bigg (}{\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}-{\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}{\bigg )}d^{2}x$

And the condition for least time is,

${\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}={\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}$

which agrees with Johann's assumption based on the law of refraction.

La solució de Newton

Introducció

20- In June 1696, Johann Bernoulli had used the pages of the Acta Eruditorum Lipsidae to pose a challenge to the international mathematical community: to find the form of the curve joining two fixed points so that a mass will slide down along it, under the influence of gravity alone, in the minimum amount of time. The solution was originally to be submitted within six months. At the suggestion of Leibniz, Bernoulli extended the challenge until Easter 1697, by means of a printed text called "Programma", published in Groningen, in the Netherlands.

19- The Programma is dated 1 January 1697, in the Gregorian Calendar. This was 22 December 1696 in the Julian Calendar, in use in Britain. 18- According to Newton's niece, Catherine Conduitt, Newton learned of the challenge at 4 pm on 29 January and had solved it by 4 am the following morning. His solution, communicated to the Royal Society, is dated 30 January. This solution, later published anonymously in the Philosophical Transactions, is correct but does not indicate the method by which Newton arrived at his conclusion. Bernoulli, writing to Henri Basnage in March 1697, indicated that even though its author, "by an excess of modesty", had not revealed his name, yet even from the scant details supplied it could be recognised as Newton's work, "as the lion by its claw" (in Latin, ex ungue Leonem).

17- D. T. Whiteside characteristically explains the origin of the Latin expression, originally from Greek, in considerable detail. The letter in French has ‘ex ungue Leonem’ preceded by the French word ‘comme’. The much quoted version ‘tanquam ex ungue Leonem’ is due to David Brewster’s book on the life and works of Newton in 1855. Bernoulli's intention was simply that he could tell the anonymous solution was Newton’s, just as it was possible to tell that an animal was a lion given its claw. It was not meant to suggest that Bernoulli considered Newton to be the lion among mathematicians, as it has since come to be interpreted.

16- John Wallis, who was 80 years old at the time, had learned of the problem in September 1696 from Johann Bernoulli's youngest brother Hieronymus, and had spent three months attempting a solution before passing it in December to David Gregory, who also failed to solve it. After Newton had submitted his solution, Gregory asked him for the details and made notes from their conversation. These can be found in the University of Edinburgh Library, manuscript A $78^{1}$, dated 7 March 1697. Either Gregory did not understand Newton's argument, or Newton's explanation was very brief. However, it is possible, with a high degree of confidence, to construct Newton's proof from Gregory's notes, by analogy with his method to determine the solid of minimum resistance (Principia, Book 2, Proposition 34, Scholium 2). A detailed description of his solution of this latter problem is included in the draft of a letter in 1694, also to David Gregory. In addition to the minimum time curve problem, there was a second problem that Newton also solved at the same time. Both solutions appeared anonymously in Philosophical Transactions of the Royal Society, for January 1697.

El problema de la braquistòcrona

Bernoulli Challenge to Newton 1

15- Fig. 1, shows Gregory’s diagram (except the additional line IF is absent from it, and Z, the start point has been added). The curve ZVA is a cycloid and CHV is its generating circle. Since it appears that the body is moving upward from e to E, it must be assumed that a small body is released from Z and slides along the curve to A, without friction, under the action of gravity.

14- Consider a small arc eE, which the body is ascending. Assume that it traverses the straight line eL to point L, horizontally displaced from E by a small distance, o, instead of the arc eE. Note, that eL is not the tangent at e, and that o is negative when L is between B and E. Draw the line through E parallel to CH, cutting eL at n. From a property of the cycloid, En is the normal to the tangent at E, and similarly the tangent at E is parallel to VH.

13- Since the displacement, EL is small it differs little in direction from the tangent at E so that the angle EnL is close to a right-angle. In the limit as the arc eE approaches zero, eL becomes parallel to VH, provided o is small compared to eE making the triangles EnL and CHV similar.

12- Also en approaches the length of chord eE, and the increase in length, $eL-eE=nL={\frac {o.CH}{CV}}$, ignoring terms in $o^{2}$ and higher, which represent the error due to the approximation that eL and VH are parallel.

The speed along eE or eL can be taken as that at E, proportional to ${\sqrt {CB}}$, which is as CH, since $CH={\sqrt {CB.CV}}$

This appears to be all that Gregory’s note contains.

Let t be the additional time to reach L,

$t\propto {\frac {nL}{\sqrt {CB}}}={\frac {o.CH}{CV.{\sqrt {CB}}}}={\frac {o}{\sqrt {CV}}}$

11- Therefore, the increase in time to traverse a small arc displaced at one endpoint depends only on the displacement at the endpoint and is independent of the position of the arc. However, by Newton’s method, this is just the condition required for the curve to be traversed in the minimum time possible. Therefore, he concludes that the minimum curve must be the cycloid.

Ell argumenta el següent:

10- Assuming now that Fig. 1 is the minimum curve not yet determined, with vertical axis CV, and the circle CHV removed, and Fig. 2 shows part of the curve between the infinitesimal arc eE and a further infinitesimal arc Ff a finite distance along the curve. The extra time, t, to traverse eL (rather than eE) is nL divided by the speed at E (proportional to ${\sqrt {CB}}$), ignoring terms in $o^{2}$ and higher:

$t\propto {\frac {o.DE}{eE.{\sqrt {CB}}}}$,

9- At L the particle continues along a path LM, parallel to the original EF, to some arbitrary point M. As it has the same speed at L as at E, the time to traverse LM is the same as it would have been along the original curve EF. At M it returns to the original path at point f. By the same reasoning, the reduction in time, T, to reach f from M rather than from F is

$T\propto {\frac {o.FG}{Ff.{\sqrt {CI}}}}$

8- The difference (t – T) is the extra time it takes along the path eLMf compared to the original eEFf :

$(t-T)\propto \left({\frac {DE}{eE{\sqrt {CB}}}}-{\frac {FG}{Ff{\sqrt {CI}}}}\right).o$ plus terms in $o^{2}$ and higher (1)

7- Because eEFf is the minimum curve, (t – T) is must be greater than zero, whether o is positive or negative. It follows that the coefficient of o in (1) must be zero:

6- ${\frac {DE}{eE{\sqrt {CB}}}}={\frac {FG}{Ff{\sqrt {CI}}}}$ (2) in the limit as eE and fF approach zero. Note since eEFf is the minimum curve it has to be assumed that the coefficient of $o^{2}$ is greater than zero.

5- Clearly there has to be 2 equal and opposite displacements, or the body would not return to the endpoint, A, of the curve.

4- If e is fixed, and if f is considered a variable point higher up the curve, then for all such points, f, ${\frac {FG}{Ff{\sqrt {CI}}}}$ is constant (equal to ${\frac {DE}{eE{\sqrt {CB}}}}$). By keeping f fixed and making e variable it is clear that ${\frac {DE}{eE{\sqrt {CB}}}}$ is also constant.

3- But, since points, e and f are arbitrary, equation (2) can be true only if ${\frac {DE}{eE{\sqrt {CB}}}}={\text{constant}}$, everywhere, and this condition characterises the curve that is sought. This is the same technique he uses to find the form of the Solid of Least Resistance.

2- For the cycloid, ${\frac {DE}{eE}}={\frac {BH}{VH}}={\frac {CH}{CV}}$ , so that ${\frac {DE}{eE{\sqrt {CB}}}}={\frac {CH}{CV.{\sqrt {CB}}}}$, which was shown above to be constant, and the Brachistochrone is the cycloid.

1- Newton gives no indication of how he discovered that the cycloid satisfied this last relation. It may have been by trial and error, or he may have recognised immediately that it implied the curve was the cycloid.

Bibliografia

• Babb, Jeff; Currie, James «The Brachistochrone Problem: Mathematics for a Broad Audience via a Large Context Problem» ( PDF) (en anglès). The Montana Mathematics Enthusiast, 5(2), 5(3), juliol 2008.
• Bernoulli, Johann «Problema novum ad cujus solutionem Mathematici invitantur" (A new problem to whose solution mathematicians are invited)» (en llatí). Acta Eruditorum, 18, juny 1696.
• Bernoulli, Johann. Mémoires de l'Académie des Sciences (en francès). 3. Acadèmia Francesa de les Ciencies, 1718. 
• Costabel, Pierre; Peiffer, Jeanne. Der Briefwechsel von Johann I Bernoulli (en alemany). Vol. II: Der Briefwechsel mit Pierre Varignon, Erster Teil: 1692-1702. Springer Basel Aktiengesellschaft, 1988. ISBN 978-3-0348-5068-1. 
• Dubois, Jacques «Chute d'une bille le long d'une gouttière cycloïdale; Tautochrone et brachistochrone; Propriétés et historique» ( PDF) (en francès). Bulletin de l'Union des Physiciens, 85(737), 1991.
• Erlichson, Herman «Johann Bernoulli's brachistochrone solution using Fermat's principle of least time» (en anglès). Eur. J. Phys., 20(5), 1999. DOI: 10.1088/0143-0807/20/5/301.
• Freguglia, P.; Giaquinta, M. The Early Period of the Calculus of Variations (en anglès), 2016. ISBN 978-3-319-38945-5. 
• Galilei, Galileo. «Third Day, Theorem 22, Prop. 36». A: Discourses regarding two new sciences, 1638.  Aquesta conclusió havia aparegut sis anys abans al Diàleg sobre els dos sistemes mundials principals de Galileu (dia 4)
• Galilei, Galileo. Dialogue Concerning the Two Chief World Systems. Ptolemaic and Copernican translated by Stillman Drake, foreword by Albert Einstein (en anglès). University of California Press Berkeley; Los Angeles, 1967. 
• Hand, Louis N.; Janet, D. «cap. 2: Variational Calculus and Its Application to Mechanics». A: Analytical Mechanics (en anglès). Cambridge: Cambridge University Press, 1998. 
• Katz, Victor J. A History of Mathematics: An Introduction (en anglès). Addison Wesley Longman, 1998. ISBN 978-0-321-01618-8. 
• Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (en anglès). Ciutat de Nova York: Broadway Books, 2003. 
• Ross, I. «The Brachistochrone Paradigm». A: Primer on Pontryagin's Principle in Optimal Control (en anglès). Collegiate Publishers, 2009. ISBN 978-0-9843571-0-9. 
• Sagan, Carl. Cosmos (en anglès). Random House Publishing Group, 2011. ISBN 9780307800985. 
• Stewart, James. «Section 10.1 - Curves Defined by Parametric Equations». A: Calculus: Early Transcendentals (en anglès). Belmont, CA: Thomson Brooks/Cole, 2012. 
• Struik, J. D.. A Source Book in Mathematics, 1200-1800 (en anglès). Harvard University Press, 1969. 
• Whiteside, Derek Thomas. The Mathematical Papers of Isaac Newton (en anglès). 8. Cambridge University Press, 2008. ISBN 978-0-521-20103-2. 

Vegeu també

• Aristotle's wheel paradox
• Identitat de Beltrami
• Càlcul de variacions
• Catenària
• Cicloide
• Newton's minimal resistance problem
• Tautochrone curve
• Trochoid

Enllaços externs

• «Brachistochrone» (en anglès). MathCurve. Amb excelents exemples animats.
• «The Brachistochrone» (en anglès). Whistler Alley Mathematics.
• «Table IV from Bernoulli's». Acta Eruditorum, 1697.
• Trott, Michael. «Brachistochrones» (en anglès). Wolfram Demonstrations Project.
• Arik, Okay. «Brachistochrone Problem» (en anglès). Wolfram Demonstrations Project.
• «The Brachistochrone problem» (en anglès). MacTutor.
• «Geodesics Revisited» ( PDF) (en anglès). Introduction to geodesics including two ways of derivation of the equation of geodesic with brachistochrone as a special case of a geodesic.
• «Brachistochrone problem in Python» (en anglès). Optimal control solution.
• «The straight line, the catenary, the brachistochrone, the circle, and Fermat» (en anglès). Unified approach to some geodesics.