Figura isogonal
 Octògon isogonal (Simetria D₄) Els eixos de simetria estan pintats en blau i vermell | |
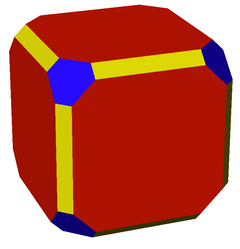 Un Cuboctàedre truncat isogonal, vist com un cub amb les seves arestes rebaixades i els seus vèrtexs truncats. (Simetria Oh) | |
En geometria, un polítop (per exemple, un polígon o un políedre, o bé una tessel·lació) és isogonal o vèrtex-transitiu si, en llenguatge planer, tots els seus vèrtexs són iguals. Això implica que cada vèrtex estigui envoltat pel mateix tipus de cares en el mateix ordre o ordre invers, i amb els mateixos angles entre les cares corresponents. D'una manera més tècnica, un polígon és isogonal quan per qualssevol dos vèrtexs existeix una simetria del polítop que fa correspondre el primer al segon de manera isomètrica. Una altra manera de dir-ho és que el grup d'automorfismes del polítop és transitiu als seus vèrtexs, o que els vèrtexs estan en una única òrbita de simetria.
El terme "isogonal" ha estat usat a bastament pels políedres, mentre que "vèrtex-transitiu" és un sinònim manllevat d'idees modernes dels camps dels grups de simetria i teoria de grafs.
2 dimensions: polígons isogonals
[modifica]Tots els polígons regulars i polígons estrellats regulars són isogonals. Alguns polígons de nombre parell de costat que alternen dos longituds de costats (com un rectangle) també ho són. Tots aquests 2n-gons tenen simetria dièdrica (Dn, n=2,3…) amb eixos de simetria que travessen els punts mitjans dels costats.
3 dimensions: políedres isogonals
[modifica]Es poden classificar els políedres isogonals:
- Regulars si també són isoèdrics (cara-transitius) i isotoxals (costat-transitius). Això implca que cada cara és el mateix tipus de polígon regular.
- Quasi-regulars si també són isotoxals (costat-transitius) però no isoèdrics (cara-transitius).
- Semiregulars si tota cara és un polígon regular però no són isoèdrics (cara-transitius) o isotoxals (costat-transitius).
- Uniformes si totes les cares són un polígon regular.
- Nobles si també són isoèdrics (cara-transitius).
N dimensions: polítops isogonals i tessel·lacions
[modifica]Les definicions anteriors es poden estendre a dimensions superiors (polítops i enrajolats). De manera més general, tots els polítops uniformes són isogonals, com, per exemple, el 4-polítop uniforme i l'enrajolat de l'espai uniforme convex.
El dual d'un polítop isogonal s'anomena isòtop, que és transitiu en les seves facetes.
Referències
[modifica]- Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 052-15-5432-2 Plantilla:Please check ISBN, p. 369 Transitivity
- Grünbaum, Branko; Shephard, G. C.. Tilings and Patterns. W. H. Freeman and Company, 1987. ISBN 0-7167-1193-1. (p. 33 k-isogonal tiling, p. 65 k-uniform tilings)
Vegeu també
[modifica]- Figura isotoxal (aresta-transitiva)
- Figura isoèdrica (cara-transitiva)
Enllaços externs
[modifica]- Weisstein, Eric W., «Vertex-transitive graph» a MathWorld (en anglès).
- Isogonal Kaleidoscopical Polyhedra Vladimir L. Bulatov, Physics Department, Oregon State University, Corvallis, Presented at Mosaic2000, Millennial Open Symposium on the Arts and Interdisciplinary Computing, 21–24 August 2000, Seattle, WA
- List of n-uniform tilings
- Weisstein, Eric W., «Demiregular tessellations» a MathWorld (en anglès). (Also uses term k-uniform for k-isogonal)
