Velocitat pròpia

Gràfic log-log de γ (blau), v/c (cian) i η (groc) en funció de la velocitat adequada w/c (és a dir, el moment p/mc). Tingueu en compte que w/c es segueix per v/c a velocitats baixes i per γ a velocitats altes. La corba vermella discontinua és γ-1 (energia cinètica K/mc²), mentre que la corba magenta discontinua és el factor Doppler relativista.

En relativitat, la velocitat pròpia (també coneguda com a celeritat) w d'un objecte en relació amb un observador és la relació entre el vector de desplaçament mesurat per l'observador ${\textbf {x}}$ i el temps adequat τ transcorregut en els rellotges de l'objecte que viatja:

${\textbf {w}}={\frac {d{\textbf {x}}}{d\tau }}$

És una alternativa a la velocitat ordinària, la distància per unitat de temps on tant la distància com el temps són mesurats per l'observador.

Els dos tipus de velocitat, ordinària i pròpia, són gairebé iguals a velocitats baixes. Tanmateix, a altes velocitats, la velocitat adequada conserva moltes de les propietats que la velocitat perd en relativitat en comparació amb la teoria newtoniana. Per exemple, la velocitat adequada és igual al moment per unitat de massa a qualsevol velocitat i, per tant, no té límit superior. A altes velocitats, com es mostra a la figura de la dreta, també és proporcional a l'energia d'un objecte.

La velocitat pròpia w es pot relacionar amb la velocitat ordinària v mitjançant el factor de Lorentz γ :

${\textbf {w}}={\frac {d{\textbf {x}}}{dt}}{\frac {dt}{d\tau }}={\textbf {v}}\,\gamma (v)$

on t és el temps de coordenades o "temps del mapa". Per al moviment unidireccional, cadascun d'ells també està relacionat simplement amb l'angle de velocitat hiperbòlica o la rapidesa η d'un objecte que es desplaça.

$\eta =\sinh ^{-1}{\frac {w}{c}}=\tanh ^{-1}{\frac {v}{c}}=\pm \cosh ^{-1}\gamma$

Introducció

Un creuer surt de l'hiperespai...

En l'espai-temps pla, la velocitat pròpia és la relació entre la distància recorreguda en relació amb un marc de mapa de referència (utilitzat per definir la simultaneïtat) i el temps propi τ transcorregut en els rellotges de l'objecte que es desplaça. És igual al moment p de l'objecte dividit per la seva massa en repòs m, i està format per les components espacials de la velocitat de quatre vectors de l'objecte. La monografia de William Shurcliff esmentava el seu ús primerenc al text de Sears i Brehme. Fraundorf ha explorat el seu valor pedagògic mentre que Ungar, Baylis i Hestenes n'han examinat la rellevància des de la teoria de grups i les perspectives de l'àlgebra geomètrica. La velocitat adequada de vegades es coneix com a celeritat.

A diferència de la velocitat de coordenades més coneguda v, la velocitat adequada és lliure de sincronia (no requereix rellotges sincronitzats) i és útil per descriure tant el moviment superrelativista com el subrelativista. Igual que la velocitat de coordenades i a diferència de la velocitat de quatre vectors, resideix en la porció tridimensional de l'espai-temps definida pel marc del mapa. Com es mostra a continuació i a la figura d'exemple de la dreta, les velocitats adequades fins i tot s'afegeixen com a tres vectors amb la reescalada del component fora del marc. Això els fa més útils per a aplicacions basades en mapes (p. ex. enginyeria) i menys útils per obtenir una visió sense coordenades. La velocitat pròpia dividida per la velocitat de la llum c és el sinus hiperbòlic de la rapidesa η, de la mateixa manera que el factor de Lorentz γ és el cosinus hiperbòlic de la rapidesa, i la velocitat de coordenades v sobre la velocitat de la llum és la tangent hiperbòlica de la rapidesa.

Imagineu un objecte que viatja per una regió de l'espai-temps descrita localment per l'equació mètrica d'espai pla d'Hermann Minkowski (cdτ)² = (cdt)² − (dx)². Aquí un marc de referència del mapa de criteris i rellotges sincronitzats defineixen la posició del mapa x i el temps del mapa t respectivament, i la d que precedeix una coordenada significa un canvi infinitesimal. Una mica de manipulació permet mostrar que la velocitat adequada w = dx/dτ = γv on com és habitual la velocitat de coordenades v = dx/dt. Així, w finit assegura que v sigui menor que la velocitat de la llum c. En agrupar γ amb v en l'expressió del moment relativista p, la velocitat pròpia també amplia la forma newtoniana del moment com a massa multiplicada per la velocitat a altes velocitats sense necessitat de massa relativista.

Fórmula adequada d'addició de velocitat

La fórmula adequada d'addició de velocitat:

$\mathbf {u} \oplus \mathbf {v} =\mathbf {u} +\mathbf {v} +\left\{{\frac {\beta _{\mathbf {u} }}{1+\beta _{\mathbf {u} }}}{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}+{\frac {1-\beta _{\mathbf {v} }}{\beta _{\mathbf {v} }}}\right\}\mathbf {u}$

on $\beta _{\mathbf {w} }$ és el factor beta donat per $\beta _{\mathbf {w} }={\frac {1}{\sqrt {1+{\frac {|\mathbf {w} |^{2}}{c^{2}}}}}}$.

Aquesta fórmula proporciona un model d'espai girovector de velocitat adequat de geometria hiperbòlica que utilitza un espai sencer en comparació amb altres models de geometria hiperbòlica que utilitzen discos o semiplans.

En el cas unidireccional, això esdevé commutatiu i es simplifica a un producte del factor de Lorentz multiplicat per una suma de velocitats de coordenades, p. ex. a w_AC = γ_ABγ_BC(v_AB + v_BC), tal com s'explica a la secció d'aplicació següent.

Aplicacions

Comparació de velocitats a alta velocitat

Suma de velocitat unidireccional: la suma adequada es corba cap amunt.

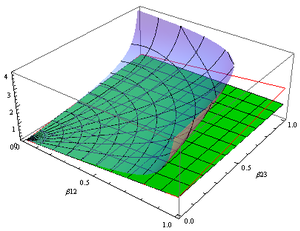
La velocitat adequada és útil per comparar la velocitat dels objectes amb el moment per unitat de massa en repòs (w) superior a la velocitat de la llum c. La velocitat de coordenades d'aquests objectes és generalment propera a la velocitat de la llum, mentre que la velocitat adequada indica la rapidesa amb què estan cobrint el terreny en els rellotges d'objectes que viatgen. Això és important, per exemple, si, com algunes partícules de raigs còsmics, els objectes que viatgen tenen una vida útil finita. La velocitat adequada també ens indica l'impuls de l'objecte, que no té límit superior.

Per exemple, un electró de 45 GeV accelerat pel Large Electron-Positron Collider (LEP) a Cern el 1989 hauria tingut un factor de Lorentz γ d'uns 88.000 (45 GeV dividit per la massa d'electrons en repòs de 511 keV). La seva velocitat de coordenades v hauria estat d'uns seixanta-quatre bilions de milions de la velocitat de la llum c a 1 segon llum per segon de mapa. D'altra banda, la seva velocitat adequada hauria estat w = γv ~ 88.000 segons de llum per segon de viatger. En comparació, la velocitat de coordenades d'un electró 250GeV al col·lisionador lineal internacional (ILC) proposat es mantindrà prop de c, mentre que la seva velocitat adequada augmentarà significativament fins a ~489.000 segons de llum per segon de viatger.

La velocitat adequada també és útil per comparar velocitats relatives al llarg d'una línia a gran velocitat. En aquest cas

${\frac {p_{AC}}{m_{1}}}=w_{AC}=\gamma _{AC}v_{AC}=\gamma _{AB}\gamma _{BC}\left(v_{AB}+v_{BC}\right)=\gamma _{AB}w_{BC}+w_{AB}\gamma _{BC}\,$

on A, B i C es refereixen a diferents objectes o marcs de referència. Per exemple, w_AC es refereix a la velocitat pròpia de l'objecte A respecte a l'objecte C. Així, en calcular la velocitat pròpia relativa, els factors de Lorentz es multipliquen quan les velocitats de coordenades sumen.

Per tant, cadascun dels dos electrons (A i C) en una col·lisió frontal a 45 GeV al marc del laboratori (B) veuria l'altre avançar cap a ells a v_AC ~ c i w_AC = 88.000² (1 + 1) ~ 1,55 × 10¹⁰ segons de llum per segon de viatger. Així, des del punt de vista de l'objectiu, els col·lisionadors poden explorar col·lisions amb una energia de projectil i un impuls per unitat de massa molt més alts.