Biàlgebra
En matemàtiques, una biàlgebra sobre un camp K és un espai vectorial sobre K que és alhora una àlgebra associativa unital i una coàlgebra coassociativa counital. [1] :46 Les estructures algebraiques i coalgebraiques es fan compatibles amb uns quants axiomes més. Concretament, la multiplicació i la unitat són tots dos homomorfismes d'àlgebra unital, o, de manera equivalent, la multiplicació i la unitat de l'àlgebra són tots dos morfismes d'àlgebra. [1] :46 (Aquests enunciats són equivalents ja que s'expressen mitjançant els mateixos diagrames commutatius.) [1] :46 [2]
Biàlgebres similars estan relacionades per homomorfismes de biàlgebra. Un homomorfisme de biàlgebra és un mapa lineal que és alhora un homomorfisme àlgebra i un homomorfisme de carbó. [3] :45
Tal com es reflecteix en la simetria dels diagrames commutatius, la definició de bialgebra és autodual, de manera que si es pot definir un dual de B (que sempre és possible si B és de dimensions finites), llavors és automàticament una bialgebra.[4]
Definició formal
[modifica](B, ∇, η, Δ, ε) és una biàlgebra sobre K si té les propietats següents: [5]
- B és un espai vectorial sobre K ;
- hi ha K-mapes lineals (multiplicació) ∇: B ⊗ B → B (equivalent a K-mapa multilineal ∇: B × B → B) i (unitat) η: K → B, tal que (B, ∇, η) és una àlgebra associativa unitària ;
- hi ha K mapes lineals (comultiplicació) Δ: B → B ⊗ B i (counitat) ε: B → K, tal que (B, Δ, ε) és una coàlgebra (coassociativa counital);
- condicions de compatibilitat expressades pels diagrames commutatius següents:
- Multiplicació ∇ i multiplicació Δ
- on τ: B ⊗ B → B ⊗ B és el mapa lineal definit per τ(x ⊗ y) = y ⊗ x per a tot x i y en B ,
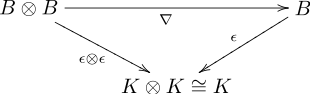
- 2.Multiplicació ∇ i counitat ε [6] :148
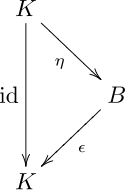
3. Multiplicació Δ i unitat η [6] :148
4. Unitat η i counitat ε [6] :148
Exemples
[modifica]Biàlgebra grupal
[modifica]Un exemple de bialgebra és el conjunt de funcions d'un grup finit G (o, de manera més general, qualsevol monoide finit) a , que podem representar com un espai vectorial que consisteix en combinacions lineals de vectors de base estàndard eg per a cada g ∈ G, que pot representar una distribució de probabilitat sobre G en el cas de vectors els coeficients dels quals són tots no negatius i sumen 1.
Altres exemples
[modifica]Altres exemples de biàlgebra inclouen l'àlgebra tensor, que es pot convertir en una biàlgebra afegint la multiplicació i la unitat apropiades; aquests es treballen amb detall en aquest article.
Bialgebras can often be extended to Hopf algebras, if an appropriate antipode can be found; thus, all Hopf algebras are examples of bialgebras.[7] Similar structures with different compatibility between the product and comultiplication, or different types of multiplication and comultiplication, include Lie bialgebras and Frobenius algebras. Additional examples are given in the article on coalgebras.[8]
Referències
[modifica]- ↑ 1,0 1,1 1,2 Kassel, 2012, p. [Biàlgebra, p. 46, a Google Books 46].
- ↑ «[https://people.math.wisc.edu/~passman/balgebra.pdf ELEMENTARY BIALGEBRA PROPERTIES OF GROUP RINGS AND ENVELOPING RINGS: AN INTRODUCTION TO HOPF ALGEBRAS]» (en anglès). [Consulta: 27 juliol 2024].
- ↑ Kassel, 2012, p. [Biàlgebra, p. 45, a Google Books 45].
- ↑ «Bialgebras and Hopf algebras» (en anglès). [Consulta: 27 juliol 2024].
- ↑ «bialgebra in nLab» (en anglès). [Consulta: 27 juliol 2024].
- ↑ 6,0 6,1 6,2 Dăscălescu, Năstăsescu i Raianu, 2001, p. [Biàlgebra, p. 148, a Google Books 148].
- ↑ Dăscălescu, Năstăsescu i Raianu, 2001, p. [Biàlgebra, p. 151, a Google Books 151].
- ↑ «Bialgebras, Frobenius algebras and associative Yang-Baxter equations for Rota-Baxter algebras» (en anglès). [Consulta: 27 juliol 2024].