Figura isoèdrica
En geometria, un polítop de dimensió 3 (un políedre) o més és isoèdric o cara-transitiu quan totes les seves cares són iguals. Més específicament, totes les cares no han de ser solament congruents sinó que han de ser transitives, és a dir, han d'estar dins de la mateixa òrbita de simetria. En altres paraules, per qualssevol cares A i B, hi ha d'haver una simetria del sòlid sencer per rotacions i reflexions que mapegi A sobre B. Per aquesta raó, els políedres isoèdrics convexos són aquelles figures que poden constituir un dau just.[1]
Els políedres isoèdrics s'anomenen isòedres (o isoedres). Poden ser descrits per la seva configuració de cares. Una figura isoèdrica amb vèrtexs regulars també és aresta-transitiva (isotoxal) i es diu que és un políedre dual quasiregular: alguns teòrics veuen aquestes figures com a verament quasiregulars perquè comparteixen les mateixes simetries, però això generalment no és acceptat.
Un políedre que és isoèdric té un dual polièdric que és vèrtex-transitiu (isogonal). Els sòlids de Catalan, les bipiràmides i els trapezòedres són tots isoèdrics. Són els duals dels sòlids arquimedians isogonals, prismes i antiprismes, respectivament. Els sòlids platònics, que són o bé auto-duals o duals amb un altre sòlid platònic, són vèrtex-, aresta- i cara-transitius (isogonals, isotoxals i isoèdrics). Un políedre que és a la vegada isoèdric i isogonal es diu que és un políedre noble.
Exemples
[modifica]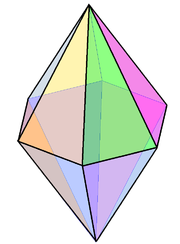 La bipiràmide hexagonal, V4.4.6, és un exemple no-regular de políedre isoèdric. |
 La tessel·lació pentagonal del Caire isoèdrica, V3.3.4.3.4 |
 L'enrajolat dodecaèdric ròmbic és un exemple d'un enrajolat isoèdric (i isocòric) que emplena l'espai |
Referències
[modifica]- ↑ McLean, K. Robin «Dungeons, dragons, and dice». The Mathematical Gazette, 74, 469, 1990, p. 243–256.
Bibliografia
[modifica]- Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 367 Transitivity
Vegeu també
[modifica]- Figura isogonal (vèrtex-transitiva)
- Figura isotoxal (aresta-transitiva)
Enllaços externs
[modifica]- Weisstein, Eric W., «Isohedron» a MathWorld (en anglès).
