Distribució normal esbiaixada

Distribució normal esbiaixada

Funció de densitat de probabilitat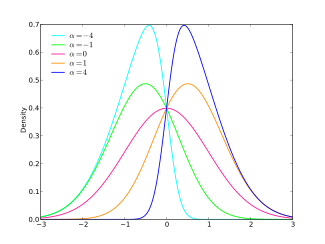
Funció de distribució de probabilitat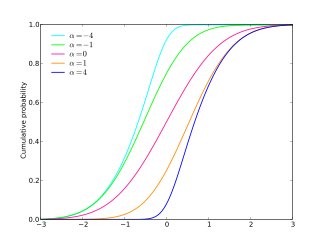
Tipus	distribució univariant i distribució de probabilitat contínua
Paràmetres	$\xi \,$ lloc (real) $\omega \,$ scale (positive, real) $\alpha \,$ forma (real)
Suport	$x\in (-\infty ;+\infty )\!$
FD	$\Phi \left({\frac {x-\xi }{\omega }}\right)-2T\left({\frac {x-\xi }{\omega }},\alpha \right)$ $T(h,a)$ is Owen's T function
Moda	$\xi +\omega m_{o}(\alpha )$
Variància	$\omega ^{2}\left(1-{\frac {2\delta ^{2}}{\pi }}\right)$
Curtosi	$2(\pi -3){\frac {\left(\delta {\sqrt {2/\pi }}\right)^{4}}{\left(1-2\delta ^{2}/\pi \right)^{2}}}$
FGM	$M_{X}\left(t\right)=2\exp \left(\xi t+{\frac {\omega ^{2}t^{2}}{2}}\right)\Phi \left(\omega \delta t\right)$

En teoria i estadística de probabilitats, la distribució normal esbiaixada és una distribució de probabilitat contínua que generalitza la distribució normal per permetre una asimetria diferent de zero.

Definició

Deixar $\phi (x)$ denoteu la funció de densitat de probabilitat normal estàndard

$\phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}$

amb la funció de distribució acumulada donada per

$\Phi (x)=\int _{-\infty }^{x}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$

on "erf" és la funció d'error. A continuació, la funció de densitat de probabilitat (pdf) de la distribució asiàtica amb el paràmetre $\alpha$ està donat per

$f(x)=2\phi (x)\Phi (\alpha x).\,$

Aquesta distribució va ser introduïda per primera vegada per O'Hagan i Leonard (1976). Les formes alternatives a aquesta distribució, amb la corresponent funció quantil, han estat donades per Ashour i Abdel-Hamid i per Mudholkar i Hutson.

Un procés estocàstic que sustenta la distribució va ser descrit per Andel, Netuka i Zvara (1984). Tant la distribució com els fonaments del seu procés estocàstic eren conseqüències de l'argument de la simetria desenvolupat a Chan i Tong (1986), que s'aplica a casos multivariants més enllà de la normalitat, per exemple, la distribució t multivariada sesgada i altres. La distribució és un cas particular d'una classe general de distribucions amb funcions de densitat de probabilitat de la forma $f(x)=2\phi (x)\Phi (x)$ on $\phi (\cdot )$ és qualsevol PDF simètric sobre zero i $\Phi (\cdot )$ és qualsevol CDF el PDF del qual és simètric sobre zero.