Efecte Hall quàntic
L’efecte Hall quàntic (o efecte Hall quàntic enter) és una versió quantificada de l’efecte Hall que s'observa en sistemes electrònics bidimensionals sotmesos a baixes temperatures i camps magnètics forts, en els quals la resistència Hall Rxy presenta passos que prenen el valors quantificats
on e és la càrrega elemental i h la constant de Planck. L'efecte Hall quàntum es refereix a la part entera o fraccionària de l'efecte Hall quàntic. El factor conegut com el factor d'ompliment, pot prendre valors enters () o fraccionaris () i d'aquesta forma es parla de l'efecte Hall quàntic enter o fraccionari.
La característica sorprenent de l'efecte Hall quàntic enter és la persistència de la quantificació (és a dir, l'altiplà de Hall) a mesura que varia la densitat d'electrons. Com que la densitat electrònica es manté constant quan el nivell de Fermi es troba en un buit espectral net, aquesta situació correspon a una en què el nivell de Fermi és una energia amb una densitat finita d'estats, tot i que aquests estats estan localitzats.[1]
L’efecte Hall quàntic fraccionari és més complicat i encara es considera un problema de recerca obert.[2] La seva existència es basa fonamentalment en les interaccions electró-electró. El 1988, es va proposar que hi havia un efecte Hall quàntic sense nivells de Landau. Aquest efecte Hall quàntic s'anomena efecte Hall anòmal quàntic (QAH). També hi ha un nou concepte de l’efecte Hall d'espín quàntic que és un anàleg de l'efecte Hall quàntic, on els corrents d'espín flueixen en lloc de corrents de càrrega.[3]
La quantificació de la conductància Hall té la important propietat de ser extremadament precisa. Els mesuraments de la conductància Hall s'ha trobat que se situen com múltiples enters o fraccions d’e²/h de gairebé una part per mil milions. Aquest fenomen rep el nom de "quantització exacta", que va ser descoberta per Klaus von Klitzing, i permet una nova definició estàndard de la resistència elèctrica basada en la resistència quàntica.[4] Des de 1990, un valor convencional fix de RK-90 es fa servir, a tot el món, en el calibratge de les resistències elèctriques.[5] L'efecte Hall quàntum també permet una determinació extremadament precisa de la constant d'estructura fina una quantitat d'importància fonamental en l'electrodinàmica quàntica.
Aplicacions
[modifica]La quantificació de la conductància de Hall () té la propietat important de ser extremadament precís. S'ha trobat que les mesures reals de la conductància de Hall són múltiples enters o fraccionaris d'e2/h a gairebé una part en mil milions. Ha permès la definició d'un nou estàndard pràctic per a la resistència elèctrica, basat en el quàntic de resistència donat per la constant de von Klitzing RK. Això rep el nom de Klaus von Klitzing, el descobridor de la quantització exacta. L'efecte Hall quàntic també proporciona una determinació independent extremadament precisa de la constant d'estructura fina, una quantitat d'importància fonamental en l'electrodinàmica quàntica.
El 1990, un valor convencional fix {{Math|RK-90 = 25.812,807 Ω. Es va definir RK-90 = 25.812,80745 Ω per al seu ús en calibracions de resistència a tot el món. [5] El 16 de novembre de 2018, la 26a reunió de la Conferència General de Peses i Mesures va decidir fixar els valors exactes de h (la constant de Planck) i e (la càrrega elemental),[6] substituint el valor de 1990 amb un valor permanent exacte.
Estat de la investigació
[modifica]La sala quàntica enter es considera part de la quantificació exacta.[7] La quantificació exacta en general no s'entén completament, però s'ha explicat com una manifestació molt subtil de la combinació del principi d’invariància de gauge juntament amb una altra simetria (vegeu Anomalies). En canvi, la sala quàntica entera es considera un problema de recerca resolt[8] i s'entén en l'àmbit de la fórmula TKNN i els Lagrangians de Chern-Simons..
L’efecte Hall quàntic fraccionari encara es considera un problema de recerca obert.[2] L'efecte Hall quàntic fraccionari també es pot entendre com un efecte Hall quàntic enter, encara que no d'electrons sinó de compostos de flux de càrrega coneguts com a fermions compostos.[9] També existeixen altres models per explicar l'efecte Hall quàntic fraccionari.[10] Actualment es considera un problema d'investigació obert perquè no existeix una llista única, confirmada i consensuada de nombres quàntics fraccionaris, ni un únic model acordat per explicar-los tots, tot i que hi ha aquestes afirmacions en l'àmbit dels fermions compostos i dels Chern-Simons no abelians. Lagrangians.
Efecte Hall quàntic enter
[modifica]Nivells de Landau
[modifica]En dues dimensions, quan els electrons clàssics estan sotmesos a un camp magnètic segueixen òrbites circulars de ciclotró. Quan el sistema es tracta de manera mecànica quàntica, aquestes òrbites es quantifiquen. Per determinar els valors dels nivells d'energia s'ha de resoldre l'equació de Schrödinger.'
Com que el sistema està sotmès a un camp magnètic, s'ha d'introduir com un potencial vectorial electromagnètic a l’equació de Schrödinger. El sistema considerat és un gas d'electrons que és lliure de moure's en les direccions x i y, però està estretament confinat en la direcció z. Aleshores, s'aplica un camp magnètic en la direcció z i, segons el calibre de Landau, el potencial del vector electromagnètic és i el potencial escalar és . Així l'equació de Schrödinger per a una partícula de càrrega i massa efectiva en aquest sistema és:
on és el moment canònic, que és substituït per l'operador i és l'energia total.
Per resoldre aquesta equació és possible separar-la en dues equacions ja que el camp magnètic només afecta el moviment al llarg dels eixos x i y. L'energia total es converteix llavors en la suma de dues contribucions . Les equacions corresponents a l'eix z són:
Per simplificar les coses, la solució es considera un pou infinit. Així, les solucions per a la direcció z són les energies , i les funcions d'ona són sinusoïdals. Per al i direccions, la solució de l'equació de Schrödinger es pot triar com el producte d'una ona plana en -direcció amb alguna funció desconeguda de , és a dir, . Això es deu al fet que el potencial vectorial no depèn de i l'operador d'impuls per tant commuta amb l'hammiltonià. Substituint aquest Ansatz a l'equació de Schrödinger s'obté l'equació de l'oscil·lador harmònic unidimensional centrada a .
on es defineix com la freqüència del ciclotró i la longitud magnètica. Les energies són:
- ,
I les funcions d'ona per al moviment en el pla estan donades pel producte d'una ona plana en i polinomis d'Hermite atenuats per la funció gaussiana en , que són les funcions d'ona d'un oscil·lador harmònic.
A partir de l'expressió dels nivells de Landau s'adona que l'energia només depèn de , no encès . Estats amb el mateix però diferent són degenerats.
Densitat d'estats
[modifica]A camp zero, la densitat d'estats per unitat de superfície per al gas d'electrons bidimensional tenint en compte la degeneració a causa de l'espin és independent de l'energia.
- .
A mesura que el camp s'encén, la densitat d'estats s'enfonsa de la constant a una pinta de Dirac, una sèrie de Dirac. funcions, corresponents als nivells de Landau separats . A temperatura finita, però, els nivells de Landau adquireixen una amplada ser el temps entre esdeveniments de dispersió. Normalment s'assumeix que la forma precisa dels nivells de Landau és un perfil gaussià o lorentzian.
Una altra característica és que les funcions d'ona formen tires paral·leles al -direcció espaiada igualment al llarg de la -eix, al llarg de les línies de . Com que no hi ha res especial en cap direcció en el -pla si el potencial vectorial s'ha escollit de manera diferent s'hauria de trobar simetria circular.
Donada una mostra de dimensions i aplicant les condicions de contorn periòdiques a la -direcció ser un nombre enter, s'obté que cada potencial parabòlic es col·loca en un valor .
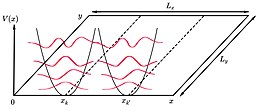
El nombre d'estats per a cada nivell de Landau i es pot calcular a partir de la relació entre el flux magnètic total que travessa la mostra i el flux magnètic corresponent a un estat.
Així, la densitat d'estats per unitat de superfície és
- .
Observeu la dependència de la densitat d'estats amb el camp magnètic. Com més gran és el camp magnètic, més estats hi ha a cada nivell de Landau. Com a conseqüència, hi ha més confinament al sistema ja que s'ocupen menys nivells d'energia.
Reescrivint l'última expressió com és evident que cada nivell de Landau conté tants estats com en un 2DEG en a .
Tenint en compte que els electrons són fermions, per a cada estat disponible en els nivells de Landau corresponen dos electrons, un electró amb cada valor del spin. . Tanmateix, si s'aplica un camp magnètic gran, les energies es divideixen en dos nivells a causa del moment magnètic associat a l'alineació del gir amb el camp magnètic. La diferència en les energies és ser un factor que depèn del material ( per als electrons lliures) i el magnetó de Bohr. La senyal es pren quan el gir és paral·lel al camp i quan és antiparal·lel. Aquest fet anomenat divisió de spin implica que la densitat d'estats per a cada nivell es redueix a la meitat. Tingues en compte que és proporcional al camp magnètic, per tant, com més gran sigui el camp magnètic, més rellevant és la divisió.

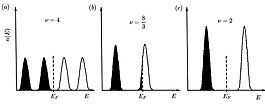
Per tal d'obtenir el nombre de nivells Landau ocupats, es defineix l'anomenat factor d'ompliment com la relació entre la densitat d'estats en un 2DEG i la densitat d'estats als nivells de Landau.
En general el factor d'ompliment no és un nombre enter. Passa a ser un nombre enter quan hi ha un nombre exacte de nivells Landau omplerts. En canvi, es converteix en un nombre no enter quan el nivell superior no està completament ocupat. En experiments reals, es fa variar el camp magnètic i es fixa la densitat electrònica (i no l'energia de Fermi!) o es varia la densitat electrònica i es fixa el camp magnètic. Tots dos casos corresponen a una variació contínua del factor d'ompliment i no es pot esperar ser un nombre enter. Des que , en augmentar el camp magnètic, els nivells de Landau augmenten en energia i el nombre d'estats de cada nivell creix, de manera que menys electrons ocupen el nivell superior fins que esdevé buit. Si el camp magnètic continua augmentant, finalment, tots els electrons estaran al nivell Landau més baix () i això s'anomena límit quàntic magnètic.
Referències
[modifica]- ↑ Editorial (en anglès) Nature, 583, 7818, 29-07-2020, pàg. 659. Bibcode: 2020Natur.583..659.. DOI: 10.1038/d41586-020-02230-7. PMID: 32728252 [Consulta: free].
- ↑ 2,0 2,1 Hansson, T.H. Reviews of Modern Physics, 89, 25005, 4-2017, pàg. 025005. arXiv: 1601.01697. Bibcode: 2017RvMP...89b5005H. DOI: 10.1103/RevModPhys.89.025005.
- ↑ Ezawa, Zyun F. Quantum Hall Effects: Recent Theoretical and Experimental Developments. 3rd. World Scientific, 2013. ISBN 978-981-4360-75-3.
- ↑ Tzalenchuk, Alexander; Lara-Avila, Samuel; Kalaboukhov, Alexei; Paolillo, Sara; Syväjärvi, Mikael; Yakimova, Rositza; Kazakova, Olga; Janssen, T. J. B. M.; Fal'Ko, Vladimir «Towards a quantum resistance standard based on epitaxial graphene». Nature Nanotechnology, 5, 3, 2010, pàg. 186–189. Bibcode: 2010NatNa...5..186T. DOI: 10.1038/nnano.2009.474. PMID: 20081845.
- ↑ «conventional value of von Klitzing constant». NIST.
- ↑ «26th CGPM Resolutions». BIPM. Arxivat de l'original el 2018-11-19. [Consulta: 19 novembre 2018].
- ↑ Franz, Marcel Science, 329, 5992, 2010, pàg. 639–640. DOI: 10.1126/science.1194123. PMID: 20689008.
- ↑ «Haldane nobel prize Lecture».
- ↑ Jainendra, Jain. Composite Fermions. Cambridge University Press, 19 abril 2012. ISBN 978-1107404250.
- ↑ Tong, David. «Quantum Hall Effect».
Bibliografia
[modifica]- Ando, Tsuneya; Matsumoto, Yukio; Uemura, Yasutada «Theory of Hall Effect in a Two-Dimensional Electron System». J. Phys. Soc. Jpn., 39, 2, 1975, pàg. 279–288. Bibcode: 1975JPSJ...39..279A. DOI: 10.1143/JPSJ.39.279.
- Klitzing, K.; Dorda, G.; Pepper, M. «New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance». Phys. Rev. Lett., 45, 6, 1980, pàg. 494–497. Bibcode: 1980PhRvL..45..494K. DOI: 10.1103/PhysRevLett.45.494.
- Laughlin, R. B. «Quantized Hall conductivity in two dimensions». Phys. Rev. B., 23, 10, 1981, pàg. 5632–5633. Bibcode: 1981PhRvB..23.5632L. DOI: 10.1103/PhysRevB.23.5632.
- Yennie, D. R. «Integral quantum Hall effect for nonspecialists». Rev. Mod. Phys., 59, 3, 1987, pàg. 781–824. Bibcode: 1987RvMP...59..781Y. DOI: 10.1103/RevModPhys.59.781.
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y. S.; Cava, R. J.; Hasan, M. Z. «A topological Dirac insulator in a quantum spin Hall phase». Nature, 452, 7190, 2008, pàg. 970–974. Bibcode: 2008Natur.452..970H. DOI: 10.1038/nature06843. PMID: 18432240.
- 25 years of Quantum Hall Effect, K. von Klitzing, Poincaré Seminar (Paris-2004). Postscript Arxivat 2007-08-24 a Wayback Machine.. Pdf Arxivat 2011-07-07 a Wayback Machine..
- Magnet Lab Press Release Quantum Hall Effect Observed at Room Temperature Arxivat 2007-12-22 a Wayback Machine.
- J. E. Avron, D. Osacdhy and R. Seiler, Physics Today, August (2003)
- Zyun F. Ezawa: Quantum Hall Effects - Field Theoretical Approach and Related Topics. World Scientific, Singapore 2008, ISBN 978-981-270-032-2
- Sankar D. Sarma, Aron Pinczuk: Perspectives in Quantum Hall Effects. Wiley-VCH, Weinheim 2004, ISBN 978-0-471-11216-7
- Baumgartner, A.; Ihn, T.; Ensslin, K.; Maranowski, K.; Gossard, A. «Quantum Hall effect transition in scanning gate experiments». Physical Review B, 76, 8, 2007. DOI: 10.1103/PhysRevB.76.085316.










![{\displaystyle \left\{{\frac {1}{2m^{*}}}\left[\mathbf {p} -q\mathbf {A} \right]^{2}+V(z)\right\}\psi (x,y,z)=\varepsilon \psi (x,y,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e35220a1ebb9bed3d0c8127c74b3467d8afdea6)




![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial z^{2}}+V(z)\right]u(z)=\varepsilon _{z}u(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69b298c0ff7c211851461c359f2e20ccb8940135)








![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m^{*}}}{\partial ^{2} \over \partial x^{2}}+{\frac {1}{2}}m^{*}\omega _{\rm {c}}^{2}(x-l_{B}^{2}k_{y})^{2}\right]u(x)=\varepsilon _{xy}u(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd0eac24c186b988302c8fd3cf4165677022af32)










































