Triangle equilàter

Triangle equilàter

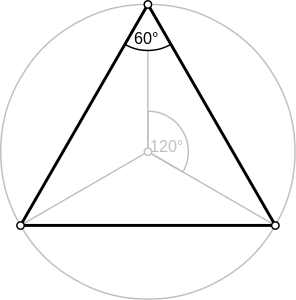Angles del triangle equilàter
Tipus	polígon regular convex, triangle isòsceles, símplex, polígon construïble, polígon equilàter, polígon equiangular i acutangle
Forma de les cares	aresta (3)
Símbol de Schläfli	{3}
Més informació
MathWorld	EquilateralTriangle

Un triangle equilàter és una figura geomètrica plana limitada per tres segments rectes d'igual longitud. És el més simple dels polígons regulars. Els seus tres angles interiors fan una mida de 60° (clar la suma dels tres ha de fer 180°), pel que els triangles equilàters són acutangles; i els exteriors fan una mida de 120°.

Un triangle equilàter pot ser dividit per una de les seves altures amb dos triangles rectangles, on els dos angles més petits fan 30°, i 60°. Si els costats de l'equilàter fan una mida d'1 unitat, l'altura fa ${\sqrt {3}}/2$, i la meitat d'un costat fa 1/2, per a la qual cosa el sinus de 30° és 1/2, i el de 60° és ${\sqrt {3}}/2$.

Els seus tres costats són iguals.

Altura

L'altura d'un triangle equilàter és

$h=L\cdot {\frac {\sqrt {3}}{2}}$

Apotema

L'apotema d'un triangle equilàter és

$a_{p}=L\cdot {\frac {\sqrt {3}}{6}}$

Perímetre

El perímetre d'un triangle equilàter de costat $L$ és

$P=3\cdot L$

Àrea

L'àrea d'un triángle equilàter és

$A={\frac {L^{2}{\sqrt {3}}}{4}}={\frac {h^{2}{\sqrt {3}}}{3}}={\frac {3R^{2}{\sqrt {3}}}{4}}=3r^{2}{\sqrt {3}}$

on $L$ és el costat; $h$, l'altura; $R$, el circumradi; $r$, l'inradi.

Altres mesures

Sigui el triangle equilàter de costat $L$, aleshores

• El radi de la circumferència circumscrita és

$R=L\cdot {\frac {\sqrt {3}}{3}}$

• El radi de la circumferència inscrita és

$r=L\cdot {\frac {\sqrt {3}}{6}}$

• El radi de la circumferència exinscrita és

$R_{e}=L\cdot {\frac {\sqrt {3}}{2}}$

• La relació entre els tres radis citats anteriorment és

$R=2\cdot r={\frac {2}{3}}\cdot R_{e}$

• També, es té la següent relació amb el costat $L$

${\frac {3}{L}}={\frac {\sqrt {25Rr-2r^{2}}}{4Rr}}$

• El semiperímetre és

$s=2R+(3{\sqrt {3}}-4)r$

Vegeu també

• Teorema de Napoleó