Quadrat (polígon)
 | |
 Model 3D | |
| Tipus | rectangle, rombe, polígon regular convex, deltoide recte, hipercub, hiperoctàedre, polígon construïble, trapezi bicèntric, trapezi tangencial recte, trapezoide mig quadrat i estel equidiagonal |
|---|---|
| Forma de les cares | aresta (4) |
| Símbol de Schläfli | {4} |
| Dual | quadrat |
| Més informació | |
| MathWorld | Square |

Un quadrat és un polígon regular de quatre costats iguals amb angles rectes (de 90°), és a dir, els seus quatre costats tenen la mateixa longitud i els seus quatre angles la mateixa mesura. Un quadrat és alhora un rombe. El fet d'imposar que, a més de tenir els quatre costats iguals i els quatre angles iguals, els angles hagin de ser de 90°, fa que només puguin existir quadrats en geometria euclidiana. Per poder estendre el concepte de quadrat a geometries no euclidianes cal relaxar la condició que els angles siguin de 90° i imposar només que siguin tots iguals.
El quadrat posseeix nombroses propietats de simetria i de regularitat. Tot quadrat té quatre eixos de simetria i és invariant per rotacions d'angles múltiples del recte. Dos costats consecutius d'un quadrat són perpendiculars, igual com les seves diagonals. Aquestes propietats són conegudes des de l'antiguitat; de fet, les primeres representacions del quadrat daten de la prehistòria. És, juntament amb la circumferència i el triangle, una de les figures geomètriques més estudiades des de l'antiguitat. El problema de la quadratura del cercle ha ocupat nombrosos matemàtics durant dos mil·lennis. El quadrat forma part de la figura descrita per Ramon Llull a La quadratura del cercle.
El «quadrat d'un nombre» designa també el producte d'aquest nombre per ell mateix. Es denota a × a = a² i es llegeix «al quadrat» o «a quadrat». Aquesta expressió s'ha imposat durant el període on l'àlgebra geomètrica era omnipresent: el quadrat d'un nombre era vist com la superfície d'un quadrat de costat el nombre inicial.
Història
[modifica]
S'han documentat atuells decorats amb quadrats datats del mil·lenni VI aC a Mesopotàmia.[1]
Hi ha tauletes que demostren el coneixement de les simetries i rotacions del quadrat cap al segle XVIII aC. La tauleta BM 15285 conté una quarantena de problemes matemàtics en relació amb àrees de figures vinculades a quadrats.[1]
El Talmud recomana construir ciutats de forma quadrada, sigui quina sigui la forma del seu recinte.[2]
Propietats
[modifica]Propietats genèriques
[modifica]- És el polígon regular de quatre costats.
- Les cares oposades d'un quadrat són paral·leles entre si.
- Un quadrat és un cas particular de rectangle, rombe, paral·lelogram, trapezi i quadrilàter.
- Les dues diagonals que el creuen són iguals i es troben al mig de la figura, propietat que s'acompleix també en determinats rombes.
- Les dues diagonals són les bisectrius dels seus angles.
- La longitud d'una diagonal és vegades la longitud d'un costat. Aquest valor, conegut com la constant de Pitàgores, va ser el primer nombre irracional que es va conèixer.
- Si un quadrilàter és alhora un rombe i un rectangle, llavors és un quadrat.
- El quadrat té l'àrea més gran que qualsevol altre quadrilàter amb el mateix perímetre.
Regular vol dir que els quatre costats són iguals i els quatre angles també. Per tant només cal demostrar que en geometria euclidiana els angles han de ser de 90 °.
Traçant una diagonal s'obtenen dos triangles. Com que la suma dels angles de cada triangle és 180 ° (vegeu Suma dels angles d'un triangle), la suma dels angles interns de qualsevol quadrilàter ha de ser 180 ° + 180 ° = 360 ° i com que en el quadrilàter regular tots quatre han de ser iguals, cada un ha de mesurar 360 °/4 = 90 °. Per tant el polígon regular de quatre costats és el quadrat.
Les cares oposades són paral·leles entre si.
Com que tots els angles són de 90 graus, les cares oposades tallen a qualsevol de les altres cares formant els mateixos angles, per tant són paral·leles.
El quadrat és un cas particular de:
- Rectangle. Quan les cares tenen la mateixa mida.
- Rombe. Quan els angles són de 90 °
- Paral·lalogram. Quan les cares tenen la mateixa mida i els angles són de 90 °
- Trapeci. Quan les cares tenen la mateixa mida i els angles són de 90 °
- Quadrilater. Quan les cares tenen la mateixa mida i els angles són de 90 °
Les diagonals són iguals i es troben al mig.
- Són iguals. Cada diagonal forma amb dos costats un triangle rectangle isòsceles del qual n'és la hipotenusa, per tant els dos angles que forma la diagonal amb cada un dels costats han de ser iguals a (180 °-90 °)/2 = 45 °. En conseqüència les dues diagonals formen triangles semblants (tenen els mateixos angles) i un dels seus costats té la mateixa longitud (costat comú). El que permet concloure que els altres costats també han de ser iguals i per tant les diagonals han de ser iguals.
- Es troben al mig. Les dues diagonals i un costat formen un triangle, cada diagonal forma un angle de 45 ° amb el costat, per tant és un triangle isòsceles, com que això passa amb els quatre triangles que es formen entre les diagonals i cada un dels quatre costats, la distància entre qualsevol vèrtex i el punt on es creuen les diagonals ha de ser sempre la mateixa.
Les diagonals són bisectrius dels seus angles. Ja s'ha vist abans que les diagonals formen angles de 45 °, com que els angles que tallen són de 90 °, en són les bisectrius (45 ° = 90 °/2).

La longitud d'una diagonal és vegades la longitud d'un costat Es pot veure pel teorema de Pitàgores, que Euclides demostra directament. Però pel cas del quadrat hi ha una demostració més senzilla que presenta el matemàtic català Savasorda en el seu Llibre de geometria abans de demostrar el teorema de Pitàgores pel cas general.
N'hi ha prou amb dibuixar el quadrat de la diagonal i observar que el triangle que forma la diagonal amb dos costats és una quarta part del quadrat de la diagonal, per tant el quadrat original (vermell) és la meitat del quadrat de la diagonal (blau) o, cosa que és el mateix el quadrat de la diagonal és el doble que el quadrat. Per tant la longitud de la diagonal és la longitud del costat.
Si un quadrilàter és alhora un rombe i un rectangle llavors és un quadrat.
Si és un rombe té els quatre costats iguals, si és un rectangle els quatre angles són angles rectes i el quadrilàter de quatre costats iguals i quatre angles rectes és per definició el quadrat.
El quadrat té l'àrea més gran que qualsevol altre quadrilàter amb el mateix perímetre.
Aquesta afirmació és fàcil d'acceptar intuïtivament però la seva demostració matemàtica no és trivial. Una demostració es pot fer seguint tres passos:
- Es demostra que prenent una diagonal i dos costats, de tots els triangles limitats per la diagonal i dos costats que mantenen constant la suma de les longituds dels dos costats el que té àrea màxima és el que té els dos costats de la mateixa longitud.
- Aplicant aquest principi a les dues diagonals és evident que donat un quadrilàter no isòsceles sempre es pot trobar un altre quadrilàter isòsceles que tingui el mateix perímetre que el primer quadrilàter i una àrea més gran.
- Llavors només cal veure que de tots els quadrilàters isòsceles el quadrat és el que té l'àrea més gran.

A la figura de la dreta s'ha representat el triangle que resulta de tallar un quadrilàter qualsevol per una de les seves diagonals. L'àrea d'aquest quadrilàter serà la meitat del producte de la base per l'altura, per tant de tots els triangles possibles que conservin constant la suma de les longituds d'aquests dos costats, el que tindrà major àrea serà el que tingui major altura. Llavors n'hi ha prou amb trobar quin és el que té una altura màxima.
Aplicant les fórmules de resolució de triangles pel cas en què es coneixen els tres constats es troba que el cosinus de l'angle α és:
i operant resulta:
per tant:
Com que l'altura és sempre un nombre positiu, trobar en quen cas l'altura és màxima és el mateix que trobar en qun cas l'altura al quadrat és màxima, i l'altura al quadrat és:
Derivant h² respecte de l s'obté:
I igualant a zero la derivada, per tal de trobar el valor de l que fa que h² sigui màxim resulta:
Per tant l'àrea és màxima quan els dos costats tenen la mateixa longitud.
Si en un quadrilàter qualsevol, es manté constant una diagonal, es pot obtenir un altre quadrilàter amb major àrea i igual perímetre si a cada cantó de la diagonal es modifiquen les longituds dels costats de forma que la suma de longituds es mantingui constant i que els dos costats tinguin la mateixa longitud. Si un cop fet això es repeteix el mateix procediment amb l'altra diagonal del quadrilàter resultant, llavors s'obté un quadrilàter isòsceles: que té tots quatre costats de la mateixa longitud.
Només cal veure que de tots els quadrilàters isòsceles el de màxima àrea és el quadrat. Com que l'àrea d'un quadrilàter isòsceles és el producte d'una base per l'altura. La base és la longitud del costat i l'altura és la longitud del costat pel sinus de l'angle. Per tant l'àrea serà màxima quan l'altura sigui màxima i l'altura serà màxima quant el sinus de l'angle sigui màxim. El sinus màxim és 1 i correspon al l'angle de 90 °. Per tant, amb un perímetre donat, el quadrilàter que tanca la màxima àrea és el quadrat.Simetries
[modifica]Sia O el punt on es creuen les dues diagonals del quadrat.
El quadrat és invariant respecte les rotacions de centre O i d'angles π/4, π/2 o π3/4; la rotació d'angle π/2 equival a una simetria central: el quadrat té per tant O com a centre de simetria. És invariant per simetria axial respecte de les bisectrius dels costats i respecte de les diagonals. El seu grup de simetria és el grup dièdric D₄.
Tota recta que passa per O divideix el quadrat en dues parts que es poden superposar.
Aquest grup es pot representar amb les següents vuit matrius:
Propietats relatives a mesures de longituds i àrees
[modifica]
A la taula de més avall es presenta el resum de les fórmules pel quadrat de costat de longitud a, aquestes fórmules resulten de les següents observacions:
- La fórmula de l'àrea s'explica observant la figura de la dreta. L'àrea de qualsevol rectangle és el producte de la base per l'altura, com que en el cas del quadrat tots els costats són iguals, l'àrea és el producte de la longitud del costat per si mateix, és a dir elevat a la segona potència. Per aquest motiu, elevar a la segona potència, s'anomena elevar al quadrat.
- La fórmula del perímetre és immediata per definició de quadrat, té quatre costats i tots quatres són d'igual longitud.
- La fórmula de la diagonal és conseqüència del teorema de Pitàgores aplicat al triangle que forma la diagonal amb dos dels costats.
- El radi de la circumferència circumscrita resulta de què el seu diàmetre és igual a la diagonal del quadrat.
- El radi de la circumferència inscrita resulta de què el seu diàmetre és igual a la longitud del costat del quadrat.

• Color blau: Circumferència circumscrita;
• Color marró: Circumferència inscrita
Fórmules del quadrat Àrea Perímetre Diagonal Radi de la circumferència circumscrita Radi de la circumferència inscrita
Construcció del quadrat
[modifica]Demostració constructiva de l'existència del quadrat
[modifica]
Euclides dona una demostració constructiva de l'existència del quadrat a la proposició 46 del llibre I dels Elements,[3] just abans de fer servir els quadrats per demostrar el teorema de Pitàgores. En la tradició didàctica moderna l'existència dels quadrats, generalment, es dona per suposada.
La demostració d'Euclides es basa en traçar les perpendiculars a un segment en els seus extrems (vegeu imatge de la dreta). Donat el segment AB, es perllonga pels dos cantons i es tracen les circumferències amb centre a A i B i radi AB per tal de trobar els punts C i D. Llavors es tracen l'arc amb centre a B i radi BC i l'arc amb centre a C i radi BC. On s'intersequen aquests dos arcs es troba el punt E que permet traçar una perpendicular a AB que passa pel punt A. Seguint el mateix procediment es troba el punt F que permet traçar la perpendicular a AB que passa pel punt B La intersecció d'aquestes perpendiculars amb les circumferències amb radi AB i centre a A i B respectivament, permet trobar els punts G i H.
Per construcció, el quadrilàter ABGH construït seguint aquest procediment compleix les següents propietats: Les distàncies AB, AG i AH són iguals i els angles GAB i ABH són de 90 °. Però per acceptar que la distància entre els dos punts nous G i H és igual a la del segment original i que els angles AGH i GHB també són de 90 °, cal admetre el cinquè postulat. Per tant l'existència de quadrats no està pas garantida en la geometria no euclidiana.
Construcció del quadrat amb compàs
[modifica]La construcció del quadrat amb compàs consisteix en trobar els seus quatre vèrtex sense fer servir el regle.

Es desitja construir el quadrat de vèrtex ABCD coneixent només els punts A i B. Sia R la distància entre A i B; llavors, es procedeix com segueix:
- Es traça C1, la circumferència de centre A i de radi R (que, per tant, conté B)
es té un tercer punt del quadrat sobre aquesta corba.
- Es traça C₂ la circumferència de centre B i de radi R (que, per tant, conté A)
el quart punt del quadrat es troba sobre aquesta corba.
- Sia G el punt d'intersecció de C1 amb C₂; es construeix llavors C₃ centrat a G i de radi R. Aquest circumferència intersecta C1 a B i en un altre punt H.
- C₄, de centre H i de radi R, interseca C1 a G i en un nou punt I.
- Sia S la distància entre G i I; es construeix llavors C₅ de centre I i de radi S (conté per força G).
- C₆ s'obté prenent per centre B i per a radi S (conté per força H). Es determina J com el punt d'intersecció entre C₆ i C₅ que està al mateix costat que G respecte a la recta AB.
- Si T és la distància entra A i J, es construeix C₇, la circumferència de centre A i de radi T (conté per força J).
El punt C s'obté per intersecció entre C₇ i C₂.
- Llavors es construeix C₈ de centre C i de radi R.
La intersecció de C₈ i C1 és el punt D.
Equacions d'un quadrat en el pla cartesià
[modifica]La superfície delimitada per un quadrat de costat 2 i centre a l'origen es pot descriure de diverses maneres. Per exemple:
El quadrat pròpiament dit és
Això també es pot escriure com
En matemàtiques, aquest quadrat representa la bola de radi unitari en el pla respecte de la p-norma quan p → ∞.
Teoremes relacionats amb el quadrat
[modifica]Teorema de Pitàgores
[modifica]
El teorema de Pitàgores estableix que en un triangle rectangle la suma dels quadrats dels catets (els costats que formen l'angle recte) és igual al quadrat de la hipotenusa (l'altre costat).
Expressat matemàticament;
- a² + b² = c²
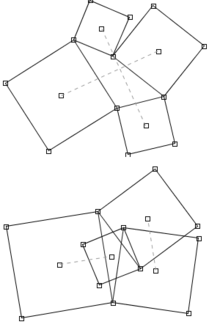

Teorema de Van Aubel
[modifica]El teorema de Van Aubel estableix que donat un quadrilàter qualsevol, si es dibuixen quatre quadrats adjacents cada un a una de les cares del quadrilàter, els segments que uneixen els centres del quadrats adjacents als costats oposats tenen la mateixa longitud i són perpendiculars entre si.
Teorema de Thébault
[modifica]El problema I del teorema de Thébault estableix que donat un paral·lelogram qualsevol si es dibuixen quatres quadrats adjacents cada d'un a un dels costats del paral·lelogram, els centres dels quadrats formen un quadrat.
Teorema de Browkin
[modifica]El teorema de Browkin estableix que per cada enter positiu n existeix un quadrat que conté exactament n punts en el seu interior d'una graella quadriculada de punts.[4]
Problema de Haberdasher
[modifica]El problema de Haberdasher consisteix en tallar un quadrat en tres talls rectes per obtenir quatre bocins que es poden tornar a compondre formant un triangle equilàter.
La solució consisteix en unir els punts mitjans de dos costats i llavors unir el punt mig d'aquest tall amb els punts mitjos dels altres dos costats, els quatre bocins es poden compondre tal com sindica a la figura.[5]

Quadratura del quadrat
[modifica]
El problema de la quadratura del quadrat consisteix en enrajolar un quadrat tal que la seva aresta mesura un nombre enter d'unitats amb quadrats que també tenen aresta de mida un nombre enter. Si no s'imposen condicions addicionals, el problema és trivial, la restricció més estudiada és la quadratura del quadrat "perfecte". Aquesta restricció consisteix en el fet que tots el quadrats han de ser de mida diferent.
El primer quadrat perfectament quadrat el va trobar Roland Sprague el 1939
El quadrat d'aresta més petita que es pot quadrar perfectament és un quadrat d'aresta 112. Observeu figura de la dreta.
Políedres amb cares quadrades
[modifica]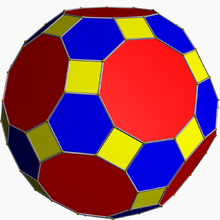
Hi ha nombrosos políedres amb cares quadrades. Els més éstudiats són els que presenten un alt grau de simetria.
Els políedres que presenten més simetries són els sòlids platònics, l'únic sòlid platònic amb cares quadrades és el cub.
Els políedres arquimedians o semiregulars són poliedres convexos les cares del qual estan formades per dos o més tipus de polígons regulars tals que els seus vèrtexs siguin homogenis. També es requereix que el políedre no sigui ni un prisma ni un antiprisma. Dels 13 políedres aquimedians que hi ha 8 tenen alguna cara quadrada: el cuboctàedre,el octàedre truncat,el petit rombicuboctàedre, el cuboctàedre truncat, el cub xato, el petit rombi-cosidodecàedre i el gran rombi-cosidodecàedre.
Hi ha infinits prismes regulars amb cares quadrades que es construeixen emprant dos polígons regulars iguals, paral·lels com a bases, separats una distància igual a la longitud de l'aresta i amb tants quadrats com arestes tenen les bases.
Els sòlids de Johnson són políedres estrictament convexos tals que totes les seves cares són polígons regulars però que no són ni un sòlids platònics, ni sòlids arquimedians, ni un prismes ni un antiprismes. Dels 92 sòlids de Johnson 74 tenen cares quadrades, per exemple la piràmide quadrada, la cúpula triangular, la piràmide triangular allargada, la piràmide quadrada giroallargada, la bipiràmide triangular allargada, la rotonda pentagonal allargada, la ortobicúpula triangular, la cúpulorotonda pentagonal giroallargada, el prisma triangular augmentat, el prisma triangular biaugmentat, el prisma hexagonal metabiaugmantat o el romboicosidodecàedre girat.
Generalitzacions
[modifica]El concepte de quadrat es pot generalitzar relaxant els axiomes de l'espai i eliminant la condició que els angles hagin de ser de 90 °, això porta als conceptes de quadrilàters regulars en geometries no euclidianes. Una altra forma de generalització és acceptar dimensions de l'espai diferents de 2.
Geometria no euclidiana
[modifica]En geometria no euclidiana, cal relaxar la condició que els angles hagin de ser necessàriament de 90 °, altrament no és possible l'existència de quadrats. Llavors els quadrats es defineixen com els polígons amb 4 costats iguals i quatre angles iguals. En geometria esfèrica, emprant aquesta definició resulta que els quadrats, a diferència dels de geometria plana tenen angles són més grans que l'angle recte.
En geometria hiperbòlica, els angles dels quadrats són més petits que l'angle recte. Com més gran és el quadrat més petits són els angles.
Exemples:
 Sis quadrats poden enrajolar l'esfera amb tres quadrats concurrents a cada vèrtex i angles interns de 120 graus. Aquesta figura s'anomena el cub esfèric. |
 Els quadrats poden enrajolar el pla euclidià amb quatre quadrats concurrents a cada vèrtex, on cada quadrat té angles interns de 90 graus. |
 Els quadrats poden enrajolar el pla hiperbòlic amb 5 quadrats concurrents a cada vèrtex, cada quadrat té angles interns de 72 graus. |
Dimensions superiors
[modifica]El quadrat és el representant en dues dimensions de dues famílies de politops: l'hipercub i el politop de creu.
L'hipercub és un politop regular amb cares mútuament perpendiculars.

|

|

| ||
| 2 dimensions Quadrat |
3 dimensions Cub |
4 dimensions Hipercub |
El politop de creu és l'embolcall convex dels vèrtexs de la forma: (±1, 0, 0, …, 0), (0, ±1, 0, …, 0), (0, 0, ±1, …, 0)..., (0, 0, 0, …, ±1).

|

|

| ||
| 2 dimensions Quadrat |
3 dimensions Octàedre |
4 dimensions 16-cel·la |
Simbologia
[modifica]Al cristianisme és una figura central. Representa la Terra i per tant també a l'home. L'origen d'aquesta associació està a una descripció del món que es troba al Gènesi.
A la figura plena de Ramon Llull que està composta per una circumferència, un quadrat i un triangle concèntrics i tots tres de la mateixa àrea. És per Ramon Llull la metàfora més acabada que representa la totalitat del ésser en totes les seves manifestacions, la divina, representada per la circumferència, la intel·lectual, representada pel triangle, i la material, representada pel quadrat. Aquí el quadrat representa la dimensió material en al·legoria als quatre elements.
Quadrat és el sobrenom que s'aplica al deu Mercuri potser, degut a la forma d'algunes de les seves estàtues primitives, o potser, perquè li estava consagrat el nombre quatre.[6]
Vegeu també
[modifica]Notes
[modifica]- ↑ 1,0 1,1 Eleanor Robson 2008
- ↑ La Bible: traduction nouvelle, 1833.
- ↑ Construcció d'un quadrat sobre un segment donat Arxivat 2011-07-09 a Wayback Machine. Els elements. Euclides. Proposició 46. Llibre I
- ↑ BrowkinsTheorem Teorema de Browkins a MathWorld
- ↑ Haberdasher's Problem El problema de Haberdasher a MathWorld
- ↑ Enciclopèdia Espasa, tomo 16, pàgina 707
Bibliografia
[modifica]- Quadrat a MathWorld (anglès)
- Eleanor Robson, Mathematics in Ancient Iraq: a Social History, Princeton University Press, 2008, 442 p. (anglès) ISBN 978-0-691-09182-2

















![{\displaystyle {\begin{matrix}R_{0}={\bigl (}{\begin{smallmatrix}1&0\\[0.2em]0&1\end{smallmatrix}}{\bigr )},&R_{1}={\bigl (}{\begin{smallmatrix}0&-1\\[0.2em]1&0\end{smallmatrix}}{\bigr )},&R_{2}={\bigl (}{\begin{smallmatrix}-1&0\\[0.2em]0&-1\end{smallmatrix}}{\bigr )},&R_{3}={\bigl (}{\begin{smallmatrix}0&1\\[0.2em]-1&0\end{smallmatrix}}{\bigr )},\\[1em]S_{0}={\bigl (}{\begin{smallmatrix}1&0\\[0.2em]0&-1\end{smallmatrix}}{\bigr )},&S_{1}={\bigl (}{\begin{smallmatrix}0&1\\[0.2em]1&0\end{smallmatrix}}{\bigr )},&S_{2}={\bigl (}{\begin{smallmatrix}-1&0\\[0.2em]0&1\end{smallmatrix}}{\bigr )},&S_{3}={\bigl (}{\begin{smallmatrix}0&-1\\[0.2em]-1&0\end{smallmatrix}}{\bigr )}.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e351df86ab2ae8858bdbaffed27c64baa6a42f)










