Teorema de Stewart

Teorema de Stewart

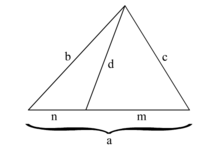
En geometria euclidiana, el teorema de Stewart estableix la relació entre la longitud dels costats d'un triangle i la longitud d'una ceviana que interseca amb el costat oposat, o amb la seva prolongació, en un punt conegut. Una ceviana és un segment del triangle que uneix un dels tres vèrtexs amb el costat oposat o la seva prolongació. El teorema afirma que, si tenim un triangle ABC i una ceviana que va des del vèrtex A fins a un punt de tall amb la recta que forma el costat a, tal que anomenem m el segment entre B i el punt de tall i n, el segment entre C i el punt de tall, llavors:

$b^{2}m+c^{2}n=a(d^{2}+mn).\,$

Tanmateix, s'ha de tenir en compte que els segments prenen valor negatiu quan no se superposen al triangle. Per aquesta raó, es pot dir que apareixerà un segment amb valor negatiu quan la ceviana intersequi la prolongació d'un costat.

El teorema de Stewart deu el seu nom al matemàtic escocès Matthew Stewart; es creu que va ser ell la primera persona que el va enunciar, l'any 1746. Tanmateix, sembla que ja fou descobert per Arquimedes de Siracusa en el segle iii aC. De totes maneres, la primera demostració matemàtica de la qual es té coneixement és la de Robert Simson, de l'any 1751.

Demostració

Construcció de la demostració

Es traça una altura h del triangle des del mateix vèrtex d'on surt la ceviana. Sense pèrdua de generalitat, assumim que el peu de l'altura cau sobre el costat de la ceviana anomenat m, tal com s'il·lustra a la dreta.

Aplicant el teorema de Pitàgores s'obtenen les equacions:

(m - z)² + h² = c² i (n+z)² + h² = b²

Desenvolupant les identitats notables:

m² - 2mz + z² + h² = c² i n² + 2nz + z² + h² = b²

Multiplicant l'equació de l'esquerra per n i la de la dreta per m:

nm² - 2mnz + nz² + nh² = nc² i mn² + 2mnz + mz² + mh² = mb²

Sumant les dues equacions:

m²n + n²m + 2mnz - 2mnz + nz² + mz² + nh² + mh² = nc² + mb²

Per procediments d'àlgebra:

(m + n)mn + (m + n)(x² + h²) = c²n + b²m

Substituint a = m + n, x² + h² = d², i per àlgebra:

amn + ad² = c²n + b²m

b²m + c²n = a(d² + mn)

I aquesta última ja és l'expressió que buscàvem.