Geometria algebraica

La geometria algebraica és una branca de les matemàtiques que combina l'àlgebra abstracta, especialment l'àlgebra commutativa, amb la geometria.

La geometria algebraica es pot comprendre com l'estudi dels conjunts de solucions dels sistemes d'equacions algebraiques. Quan hi ha més d'una variable, les consideracions geomètriques es tornen importants per entendre el fenomen. Podem dir que la matèria en comença quan abandonem la simple solució d'equacions i la qüestió de comprendre el conjunt de totes les solucions del sistema es torna tan important com trobar alguna solució. Això duu a aspectes molt sofisticats de les matemàtiques, tant conceptualment com tècnicament. En termes més tècnics, s'ocupa de l'estudi de les varietats definides per equacions polinòmiques.

Els objectes d'estudi fonamental de la geometria algebraica són les varietats algebraiques, que són manifestacions geomètriques de les solucions de sistemes d'equacions polinòmiques. Exemples de les classes més estudiades de varietats algebraiques són: corbes algebraiques, que inclouen rectes, circumferències, paràboles, el·lipses, hipèrboles, corbes cúbiques planes com ara les corbes el·líptiques, i corbes quàrtiques com la lemniscata de Bernoulli i els ovals de Cassini. Un punt del pla pertany a una corba algebraica si les coordenades satisfan una certa equació algebraica. Les qüestions més bàsiques de la geometria algebraica inclouen l'estudi de punts d'especial interès com els punts singulars d'una corba, els punts d'inflexió i els punts de l'infinit. Qüestions més avançades impliquen la topologia de la corba i les relacions entre les corbes obtingudes a partir de les diferents equacions.

La geometria algebraica ocupa un lloc central en les matemàtiques modernes i té moltes connexions conceptuals amb camps tan diversos com l'anàlisi complexa, la topologia i la teoria de nombres. Inicialment un estudi dels sistemes d'equacions polinòmiques de diferents variables, el tema de la geometria algebraica comença s'acaba la resolució d'equacions, i esdevé fins i tot més important entendre les propietat intrínseques de la totalitat de les solucions d'un sistema d'equacions que trobar una solució en particular; això porta a una de les àrees més profundes de totes les matemàtiques, tant conceptualment com tècnica.

En el segle xx, la geometria algebraica es va dividir en diverses subàrees.

El corrent principal de la geometria algebraica es dedica a l'estudi dels punts complexos de les varietat algebraiques i més en general dels punts amb coordenades en un cos algebraicament tancat.
La geometria algebraica real és l'estudi dels punts reals en una varietat algebraica.
La geometria diofàntica i, més generalment, la geometria aritmètica és l'estudi de punts d'una varietat algebraica amb coordenades en cossos que no són algebraicament tancat i que es donen en teoria de nombres algebraics, com són els cossos dels nombres racionals, dels nombres algebraics, els cossos finits, de funcions algebraiques, i el de nombres p-àdics.
Gran part de la teoria de la singularitat es dedica a l'estudi de les singularitats de les varietats algebraiques.
La geometria algebraica computacional és una àrea que va sorgir en la intersecció entre la geometria algebraica i la computació algebraica, amb l'auge de la computació. Consisteix principalment en el disseny d'algorismes i el desenvolupament de software per a l'estudi de les propietats de varietats algebraiques explícitament donades.

Gran part del desenvolupament del principal corrent de la geometria algebraica en el segle XX es va donar en el marc de l'àlgebra abstracta, amb un èmfasi creixentment centrat en les propietats "intrínseques" de les varietats algebraiques independentment de cap forma particular d'embedding de la varietat en les coordenades de l'espai ambient; sempre en paral·lel als desenvolupaments de la topologia, de la geometria diferencial i complexa. Una fita clau d'aquesta geometria algebraica abstracta és la teoria d'esquemes de Grothendieck que va permetre usar la teoria de feixos en l'estudi de varietats algebraiques de forma molt similar al seu ús en l'estudi de varietats diferenciables i analítiques. Aquest resultat s'obté estenent la noció d'un punt: en geometria algebraica clàssica, es pot identificar un punt d'una varietat afí, a través del teorema dels zeros de Hilbert, amb un ideal maximal de l'anell de coordenades, mentre que els punts de l'esquema afí corresponent són tots ideals primers de l'anell. Això significa que un punt d'aquest esquema pot ser o bé un punt usual o una subvarietat. Aquest plantejament també permet una unificació del llenguatge i de les eines de la geometria algebraica clàssica, principalment centrats en punts complexos i en la teoria de nombres algebraics. La demostració de Wiles del llargament no resolt darrer teorema de Fermat és un exemple del potencial d'aquest plantejament.

Nocions bàsiques

Zeros de polinomis simultanis of simultaneous polynomials

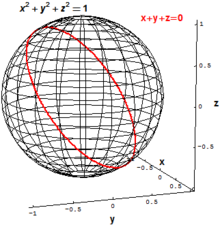
En la geometeria algebraica clàssica, el principals objectes d'interès són els conjunts de col·leccions en què polinomis desapareixen, en el sentit de tots aquells punts que satisfan simultàniament una o més equacions polinòmiques. Per exemple, l'esfera de dues dimensions de radi 1 en l'espai euclidià $\mathbb {R} ^{3}$ pot ser definit com el conjunt de tots els punts (x,y,z) tals que

x^{2}+y^{2}+z^{2}-1=0.\,

Es pot definir un cercle "inclinat" en $\mathbb {R} ^{3}$ com el conjunt de punts (x,y,z) que satisfan les equacions de dos polinomis

x^{2}+y^{2}+z^{2}-1=0,\,

x+y+z=0.\,

Varietats afins

Es parteix d'un cos k, que en geometria algebraica clàssica és sempre el dels nombres complexos $\mathbb {C}$ , tot i que gran part dels resultats a què s'arribaran també apliquen simplement assumint que k és algebraicament tancat. Es considera l'espai afí de dimensió n sobre k, anotat Aⁿ(k) (o més simplement Aⁿ, quan k és clar pel context). Quan es fixa un sistema de coordenades, es pot identificar Aⁿ(k) amb kⁿ. L'objectiu de no treballar amb kⁿ és el d'emfasitzar que hom "s'oblida" de l'estructura d'espai vectorial de kⁿ.

S'anomena a una funció f : Aⁿ → A¹ polinòmica (o regular) si pot ser escrita en forma de polinomi, és a dir, si hi ha un polinomi p en k[x₁,...,x_n] tal que f(M) = p(t₁,...,t_n) en tot punt M amb coordenades (t₁,...,t_n) en Aⁿ. La propietat que una funció sigui o no polinòmica (o regular) no depèn de la tria del sistema de coordenades en Aⁿ.

Quan es tria un cert sistema de coordenades, es poden identificar les funcions regulars de l'espai n-afí amb l'anell de les funcions polinòmiques en n variables sobre k. Per tant, el conjunt de les funcions regulars en Aⁿ és un anell, denotat com k[Aⁿ].

Es diu que un polinomi esvaneix en un punt si en avaluar-se en aquest punt dona zero. Sigui S el conjunt de polinomis en k[Aⁿ]. El conjunt d'esvaniment de S (en anglès vanishing set of S o zero set) és el conjunt V(S) de tots els punts en Aⁿ on tots els polinomis en S esvaneixen. Simbòlicament,

V(S)=\{(t_{1},\dots ,t_{n})\mid p(t_{1},\dots ,t_{n})=0{\text{ per tot }}p\in S\}.\,

Un subconjunt de Aⁿ que és V(S), per un cert S, és anomenat un conjunt algebraic. La V denota varietat (un tipus específic de conjunt algebraic que es definirà més endavant).

Donat un subconjunt U de Aⁿ, una bona pregunta és si es pot recuperar el conjunt de polinomis que el generen. Si U és qualsevol subconjunt de Aⁿ, es defineix I(U) com el conjunt de tots els polinomis el conjunt d'esvaniment dels quals conté U. La I denota l'ideal: si dos polinomis f i g tots dos s'esvaneixen en U, llavors f+g s'esvaneix en U, i si h és un polinomi qualsevol, llavors hf s'esvaneix en U, llavors I(U) és sempre un ideal de l'anell de polinomis k[Aⁿ].

Dues preguntes naturals que sorgeixen són

Donat un subconjunt U de Aⁿ, quan és U = V(I(U))?
Donat un conjunt de polinomis S, quan és S = I(V(S))?

S'obté resposta a la primera pregunta introduint la topologia de Zariski, una topologia en Aⁿ els conjunts tancats del qual són conjunts algebraics, i que reflecteix directament l'esctructura algebraica de k[Aⁿ]. Llavors U = V(I(U)) si i només si U és un conjunt algebraic o, equivalentment, un conjunt tancat de Zariski. La resposta a la segona pregunta ve donada pel teorema dels zeros de Hilbert. En una de les seves formes, diu que I(V(S)) és el radical de l'ideal generat per S. En llenguatge més abstracte, hi ha una connexió de Galois, que dona lloc a dos operadors de cloenda; poden ser identificats, i naturalment tenen un paper important en la teoria; vegeu l'example.

Per diferents raons, pot ser que no sempre es vulgui treballar amb l'idela complet que correspon a un conjunt algebraic U. El teorema de la base de Hilbert implica que els ideals en k[Aⁿ] sempre són generats finitament.

Un conjunt algebraic és irreductible si no pot ser escrit com la unió de dos conjunts algebraics més petits. Tot conjunt algebraic és una unió finita de conjunts algebraics irreductibles amb un descomposició única. Així doncs, els seus elements són anomenats els components irreductibles del conjunt algebraic. Un conjunt algebraic irreductible és també anomenat varietat. Resulta que un conjunt algebraic és una varietat si i només si pot ser definit com el conjunt d'esvaniment d'un ideal primer d'un anell polinòmic.

Alguns autors no distingeixen de forma clara entre conjunts algebraics i varietat i utilitzen el terme varietat irreductible per fer-ne la distinció quan cal.

Història

Abans del segle XVI

Algunes de les arrels de la geometria algebraica daten del treball dels grecs hel·lènics del segle V a.C. El problema delià, per exemple, consistia a construir una longitud x tal que el cub de costat x contingui el mateix volum que el paral·lelepípede a²b donats els costats a i b. Menecme (circa 350 a.C.) va considerar el problema geomètricament fent intersecar la parella de plans cònics ay = x² i xy = ab.^[1] Al segle iii aC, Arquimedes i Apol·loni van estudiar sistemàticament problemes addicionals sobre seccions còniques usant coordenades.^[1]^[2] Matemàtics àrabs medievals, com ara Ibn al-Hàytham en el segle x,^[3] van solucionar algunes equacions cúbiques per mitjans purament algebraics i posteriorment van interpretar els resultats geomètricament. El matemàtic persa Omar Khayyam (nascut l'any 1048) va descobrir un mètode per solucionar equacions de tercer grau fent intersecar un paràbola amb un cercle^[4] i sembla que va ser el primer a concebre una teoria general d'equacions cúbiques.^[5] Uns anys després d'Omar Khayyam, el Tractat sobre equacions de Xàraf-ad-Din at-Tussí va ser descrit per Roshdi Rashed com la "inauguració dels inicis de la geometria algebraica".^[6] Això va ser disputat per Jeffrey Oaks, que defensa que l'estudi de corbes a partir d'equacions va originar-se amb Descartes al segle xvii.^[7]

Renaixement

Aquestes tècniques d'aplicaar construccions geomètriques als problemes algebraics també van ser adoptades per un cert nombre de matemàtics del Renaixement com ara Girolamo Cardano i Niccolo Fontana Tartaglia en els seus estudis de l'equació cúbica. La majoria dels matemàtics (notablement Blaise Pascal, que estava en contra de l'ús de mètodes algebraics i analítics en geometria) dels segles xvi i xvii van preferir el plantejament geomètric en problemes de construcció, en detriment de l'algebraic.^[8] El matemàtic francès François Viète i posteriorment René Descartes i Pierre de Fermat van revolucionar la forma convencional d'entendre la construcció de problemes a partir de la introducció de la geometria de coordenades. Es van centrar principalment en les propietats de les corbes algebraiques, com ara les definides per equacions diofàntiques (en el cas de Fermat), i en la reformulació algebraica dels treballs del grecs clàssics sobre còniques i cúbiques (en el cas de Descartes).

Durant el mateix període, Blaise Pascal i Girard Desargues van plantejar la geometria des d'una perspectiva diferent, desenvolupant les nocions sintètiques de la geometria projectiva. Pascal i Desargues també van estudiar les corbes, però des d'un punt de vista purament geomètric: l'anàleg de la construcció amb regla i compàs dels grecs. Finalment, la geometria analítica de Descartes i Fermat va prevaldre, ja que proporcionava als matemàtics del segle xviii eines quantitatives concretes que necessitaven per estudiar els problemes físics usant el càlcul, inventat recentment per Newton i Leibniz. Tanmateix, a finals del segle xviii, gran part del caràcter algebraic de la geometria analítica va ser subsumida pel càlcul infinitesimal de Lagrange i d'Euler.

Aplications

Actualment, la geometria algebraica té aplicacions en l'estadística,^[9] en la teoria de control,^[10]^[11] en la robòtica,^[12] en els codis de correcció d'errors,^[13] en la filogenètica^[14] i en el modelatge geomètric.^[15] També té connexions amb la teoria de cordes,^[16] la teoria dels jocs,^[17] l'aparellament de grafs,^[18] els solitons^[19] i la programació lineal entera.^[20]

Referències

↑ ^1,0 ^1,1 Dieudonné, Jean «The Historical Development of Algebraic Geometry». The American Mathematical Monthly, 79, 8, 1972, pàg. 827-866. DOI: 10.2307/2317664. ISSN: 0002-9890. JSTOR: 2317664. Wikidata: Q55886951.
↑ Kline, 1972, p. 108, 90.
↑ Kline, 1972, p. 193.
↑ Kline, 1972, p. 193–195.
↑ ; Robertson, E. F.«Omar Khayyam». School of Mathematics and Statistics, University of St Andrews. Arxivat de l'original el 12 novembre 2017. «Khayyam himself seems to have been the first to conceive a general theory of cubic equations.»
↑ Rashed, Roshdi. The Development Of Arabic Mathematics Between Arithmetic And Algebra. Springer, 1994, p. 102–103.
↑ Oaks, Jeffrey. «Excavating the errors in the "Mathematics" chapter of 1001 Inventions».
↑ Kline, 1972, p. 279.
↑ Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth. Lectures on Algebraic Statistics. Springer, 2009. ISBN 978-3-7643-8904-8.
↑ Falb, Peter. Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry. Springer, 1990. ISBN 978-0-8176-4113-9.
↑ Tannenbaum, Allen. Invariance and Systems Theory: Algebraic and Geometric Aspects. Volume 845. Springer-Verlag, 1982. ISBN 9783540105657.
↑ Selig, J. M.. Geometric Fundamentals of Robotics. Springer, 2005. ISBN 978-0-387-20874-9.
↑ Tsfasman, Michael A.; Vlăduț, Serge G.; Nogin, Dmitry. Algebraic Geometric Codes Basic Notions. American Mathematical Soc., 1990. ISBN 978-0-8218-7520-9.
↑ Cipra, Barry Arthur «Algebraic Geometers See Ideal Approach to Biology». SIAM News, 40, 6, 2007. Arxivat de l'original el 3 març 2016. Arxivat 2016-03-03 a Wayback Machine.
↑ Jüttler, Bert; Piene, Ragni. Geometric Modeling and Algebraic Geometry. Springer, 2007. ISBN 978-3-540-72185-7.
↑ Cox, David A.; Katz, Sheldon. Mirror Symmetry and Algebraic Geometry. American Mathematical Soc., 1999. ISBN 978-0-8218-2127-5.
↑ Blume, L. E.; Zame, W. R. «The algebraic geometry of perfect and sequential equilibrium». Econometrica, 62, 4, 1994, pàg. 783–794. DOI: 10.2307/2951732. JSTOR: 2951732.
↑ Dimers and Amoebae, 2003.
↑ Fordy, Allan P. Soliton Theory A Survey of Results. Manchester University Press, 1990. ISBN 978-0-7190-1491-8.
↑ Cox, David A.; Sturmfels, Bernd. Applications of Computational Algebraic Geometry. American Mathematical Soc.. ISBN 978-0-8218-6758-7.

Fonts

Kline, M. Mathematical Thought from Ancient to Modern Times. Volume 1. Oxford University Press, 1972. ISBN 0195061357.
Dieudonné, Jean. A Panoroma of Pure Mathematics. Nova York: Academic Press, 1982.

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Geometria algebraica

[Dieudonné-1] 1,0 ^1,1 Dieudonné, Jean «The Historical Development of Algebraic Geometry». The American Mathematical Monthly, 79, 8, 1972, pàg. 827-866. DOI: 10.2307/2317664. ISSN: 0002-9890. JSTOR: 2317664. Wikidata: Q55886951.

[FOOTNOTEKline1972108,_90-2] Kline, 1972, p. 108, 90.

[FOOTNOTEKline1972193-3] Kline, 1972, p. 193.

[FOOTNOTEKline1972193–195-4] Kline, 1972, p. 193–195.

[5] ; Robertson, E. F.«Omar Khayyam». School of Mathematics and Statistics, University of St Andrews. Arxivat de l'original el 12 novembre 2017. «Khayyam himself seems to have been the first to conceive a general theory of cubic equations.»

[6] Rashed, Roshdi. The Development Of Arabic Mathematics Between Arithmetic And Algebra. Springer, 1994, p. 102–103.

[7] Oaks, Jeffrey. «Excavating the errors in the "Mathematics" chapter of 1001 Inventions».

[FOOTNOTEKline1972279-8] Kline, 1972, p. 279.

[9] Drton, Mathias; Sturmfels, Bernd; Sullivant, Seth. Lectures on Algebraic Statistics. Springer, 2009. ISBN 978-3-7643-8904-8.

[10] Falb, Peter. Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry. Springer, 1990. ISBN 978-0-8176-4113-9.

[11] Tannenbaum, Allen. Invariance and Systems Theory: Algebraic and Geometric Aspects. Volume 845. Springer-Verlag, 1982. ISBN 9783540105657.

[12] Selig, J. M.. Geometric Fundamentals of Robotics. Springer, 2005. ISBN 978-0-387-20874-9.

[13] Tsfasman, Michael A.; Vlăduț, Serge G.; Nogin, Dmitry. Algebraic Geometric Codes Basic Notions. American Mathematical Soc., 1990. ISBN 978-0-8218-7520-9.

[14] Cipra, Barry Arthur «Algebraic Geometers See Ideal Approach to Biology». SIAM News, 40, 6, 2007. Arxivat de l'original el 3 març 2016. Arxivat 2016-03-03 a Wayback Machine.

[15] Jüttler, Bert; Piene, Ragni. Geometric Modeling and Algebraic Geometry. Springer, 2007. ISBN 978-3-540-72185-7.

[16] Cox, David A.; Katz, Sheldon. Mirror Symmetry and Algebraic Geometry. American Mathematical Soc., 1999. ISBN 978-0-8218-2127-5.

[17] Blume, L. E.; Zame, W. R. «The algebraic geometry of perfect and sequential equilibrium». Econometrica, 62, 4, 1994, pàg. 783–794. DOI: 10.2307/2951732. JSTOR: 2951732.

[18] Dimers and Amoebae, 2003.

[19] Fordy, Allan P. Soliton Theory A Survey of Results. Manchester University Press, 1990. ISBN 978-0-7190-1491-8.

[20] Cox, David A.; Sturmfels, Bernd. Applications of Computational Algebraic Geometry. American Mathematical Soc.. ISBN 978-0-8218-6758-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]