Modelatge sòlid

El modelatge de sòlids (o modelatge de sòlids) és un conjunt coherent de principis per al modelatge matemàtic i informàtic de formes tridimensionals (sòlids). El modelatge sòlid es distingeix dins de les àrees més àmplies relacionades amb el modelatge geomètric i els gràfics per ordinador, com ara el modelatge 3D, pel seu èmfasi en la fidelitat física.[1] En conjunt, els principis del modelatge geomètric i sòlid formen la base del disseny assistit per ordinador en 3D i, en general, donen suport a la creació, intercanvi, visualització, animació, interrogació i anotació de models digitals d'objectes físics.
Visió general
[modifica]L'ús de tècniques de modelatge sòlid permet el procés d'automatització de diversos càlculs d'enginyeria difícils que es realitzen com a part del procés de disseny. La simulació, la planificació i la verificació de processos com el mecanitzat i el muntatge van ser un dels principals catalitzadors per al desenvolupament del modelatge de sòlids. Més recentment, la gamma d'aplicacions de fabricació compatibles s'ha ampliat molt per incloure la fabricació de xapa, modelat per injecció, soldadura, encaminament de canonades, etc. Més enllà de la fabricació tradicional, les tècniques de modelatge sòlid serveixen com a base per a la creació de prototips ràpids, l'arxiu de dades digitals i l'enginyeria inversa. mitjançant la reconstrucció de sòlids a partir de punts mostrejats en objectes físics, anàlisi mecànica utilitzant elements finits, planificació del moviment i verificació del recorregut NC, anàlisi cinemàtica i dinàmica de mecanismes, etc. Un problema central en totes aquestes aplicacions és la capacitat de representar i manipular eficaçment la geometria tridimensional d'una manera coherent amb el comportament físic dels artefactes reals. La investigació i el desenvolupament de models sòlids han abordat eficaçment molts d'aquests problemes i continua sent un focus central de l'enginyeria assistida per ordinador.
Fonaments matemàtics
[modifica]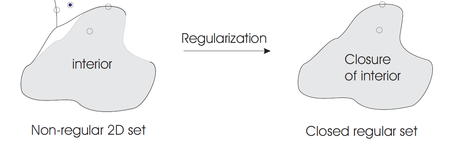
La noció de modelatge sòlid tal com es practica avui en dia es basa en la necessitat específica de completesa informativa en els sistemes de modelatge geomètric mecànic, en el sentit que qualsevol model informàtic hauria de suportar totes les consultes geomètriques que es puguin demanar al seu objecte físic corresponent. El requisit reconeix implícitament la possibilitat de diverses representacions informàtiques del mateix objecte físic sempre que dues d'aquestes representacions siguin coherents. És impossible verificar computacionalment la integritat informativa d'una representació tret que la noció d'objecte físic es defineixi en termes de propietats matemàtiques computables i independentment de qualsevol representació particular. Aquest raonament va portar al desenvolupament del paradigma de modelització que ha donat forma al camp del modelatge sòlid tal com el coneixem avui.[2]
Tots els components fabricats tenen una mida finita i uns límits ben comportats, de manera que inicialment es va centrar en el modelatge matemàtic de peces rígides fetes de material isotròpic homogeni que es podien afegir o eliminar. Aquestes propietats postulades es poden traduir en propietats de regions, subconjunts de l'espai euclidià tridimensional. Els dos enfocaments comuns per definir la "solidesa" es basen en la topologia de conjunt de punts i la topologia algebraica, respectivament. Tots dos models especifiquen com es poden construir sòlids a partir de peces o cel·les simples.
Segons el model de solidesa de conjunt de punts continu, tots els punts de qualsevol X ⊂ ℝ3 es poden classificar segons els seus entorns respecte a X com a punts interiors, exteriors o límit. Suposant que ℝ3 està dotat de la mètrica euclidiana típica, un veïnatge d'un punt p ∈ X pren la forma d'una bola oberta. Perquè X es consideri sòlid, cada veïnatge de qualsevol p ∈ X ha de ser consistentment tridimensional; punts amb barris de dimensions inferiors indiquen manca de solidesa. Es garanteix l'homogeneïtat dimensional dels barris per a la classe dels conjunts regulars tancats, definits com els conjunts iguals al tancament del seu interior. Qualsevol X ⊂ ℝ3 es pot convertir en un conjunt regular tancat o "regularitzat" prenent el tancament del seu interior i, per tant, l'espai de modelització dels sòlids es defineix matemàticament com l'espai dels subconjunts regulars tancats de ℝ3 (per Heine -Teorema de Borel s'implica que tots els sòlids són conjunts compactes). A més, cal tancar els sòlids sota les operacions booleanes d'unió conjunta, intersecció i diferència (per garantir la solidesa després de l'addició i eliminació de material). L'aplicació de les operacions booleanes estàndard a conjunts regulars tancats pot no produir un conjunt regular tancat, però aquest problema es pot resoldre regularitzant el resultat de l'aplicació de les operacions booleanes estàndard. Les operacions de conjunts regularitzats es denoten ∪ ∗, ∩ ∗ i − ∗.
La caracterització combinatòria d'un conjunt X ⊂ ℝ3 com a sòlid implica representar X com un complex cel·lular orientable de manera que les cel·les proporcionin adreces espacials finites per a punts en un continu d'altra manera innombrable.[3] La classe de subconjunts acotats semianalítics de l'espai euclidià es tanca sota operacions booleanes (estàndards i regularitzades) i presenta la propietat addicional que cada conjunt semianalític es pot estratificar en una col·lecció de cel·les disjuntives de dimensions 0,1,2,3.. Una triangulació d'un conjunt semianalític en una col·lecció de punts, segments de línia, cares triangulars i elements tetraèdrics és un exemple d'estratificació que s'utilitza habitualment. El model combinatori de solidesa es resumeix llavors dient que, a més de ser subconjunts acotats semianalítics, els sòlids són poliedres topològics tridimensionals, concretament varietats orientables tridimensionals amb límit.[4] En particular, això implica que la característica d'Euler de la frontera combinatòria [5] del poliedre és 2. El model de la varietat combinatòria de solidesa també garanteix que el límit d'un sòlid separa l'espai exactament en dos components com a conseqüència del teorema de Jordan-Brouwer, eliminant així conjunts amb barris no múltiples que es consideren impossibles de fabricar.
El conjunt de punts i els models combinatoris de sòlids són totalment coherents entre si, es poden utilitzar de manera intercanviable, basant-se en propietats contínues o combinatòries segons sigui necessari, i es poden estendre a n dimensions. La propietat clau que facilita aquesta consistència és que la classe de subconjunts regulars tancats de ℝn coincideix precisament amb poliedres topològics n-dimensionals homogenis. Per tant, cada sòlid n-dimensional pot ser representat sense ambigüitats pel seu límit i el límit té l'estructura combinatòria d'un poliedre n-1-dimensional que té veïnatges n-1-dimensionals de manera homogènia.
Referències
[modifica]- ↑ Shapiro, Vadim. Solid Modeling (en anglès). Elsevier, 2001.
- ↑ Requicha, A.A.G; Voelcker, H. IEEE Computer Graphics and Applications, 3, 7, 1983, pàg. 25–37. DOI: 10.1109/MCG.1983.263271.
- ↑ Shapiro, Vadim. Solid Modeling (en anglès). Elsevier, 2001.
- ↑ Requicha, A.A.G. ACM Computing Surveys, 12, 4, 1980, pàg. 437–464. DOI: 10.1145/356827.356833.
- ↑ Hatcher, A.. Algebraic Topology (en anglès). Cambridge University Press, 2002.
