Vés al contingut

Test de planaritat

De la Viquipèdia, l'enciclopèdia lliure

En teoria de grafs, el test de planaritat és un problema que consisteix en demostrar si un graf és pla, és a dir, si pot ser dibuixat a un pla sense que hi hagi interseccions entre les arestes. Es tracta d'un problema molt estudiat en ciències computacionals i per això té molts de possibles algorismes i optimitzacions, sovint relacionades amb la implementació de nous tipus d'estructures de dades. La majoria d'aquests mètodes operen en O(n) (temps lineal), on n és el nombre d'arestes o bé de vèrtexs del graf. En lloc d'un simple valor booleà (cert/fals), és preferible que el resultat de l'algorisme sigui una distribució planar del graf sempre que aquesta sigui possible, o bé una identificació dels obstacles de la planaritat, és a dir els subgrafs no planars. Tot i això, si un algorisme troba un subgraf no planar pot estar segur de que el resultat final no és planar i retornar-ho sense computacions addicionals.

Criteris de planaritat

[modifica]

Els tests de planaritat utilitzen teoremes i criteris que caracteritzen la planaritat d'un graf.

Teorema de Kuratowski

[modifica]
Subdivisió de K3,3 al graf de Petersen generalitzat G(9,2). Per tant segons el teorema de Kuratowski, és un graf no planar.

Un graf és planar si i només si no conté un subgraf isomorf a una subdivisió de K₅ (el graf complet de cinc vèrtexs) o K3,3 (el graf bipartit complet de sis vèrtexs).[1]

Una subdivisió del graf és un graf format al subdividir les arestes a rutes d'una o més arestes. El teorema de Kuratowski estipula que un graf G és pla si no és possible subdividir les arestes de K₅ o K3,3 i després possiblement afegir arestes i vèrtexs addicionals, per obtenir un graf isomòrfic a G. De la mateixa manera, un graf G és pla si i només si no conté un subgraf H homeomòrfic a K₅ o K3,3. A aquest subgraf H se l'anomena subgraf de Kuratowski.[2] Kuratowski també va demostrar que subdividir o escurçar un graf no en canvia la planaritat.[3] La fórmula d'Euler permet demostrar que K₅ i K3,3 no són planars, per tant qualsevol graf que els inclou no és planar.[4] Habitualment, grafs no planars contenen un gran nombre de subgrafs de Kuratowski. És possible extreure un gran nombre de subgrafs de Kuratowski en temps lineal.[5] El teorema ha estat demostrat de diverses maneres.[6][7][8]

Teorema de Wagner

[modifica]
K₅ i K3,3 com a subgrafs del graf de Petersen (cercles petits i arestes negres). Els subgrafs poden ser formats al eliminar els vèrtex vermells i escurçant les arestes en cada cercle groc.

Un graf és planar si i només si no conté el subgraf d'un escurçament que és isomòrfic a K₅ o K3,3.[9]

Si un graf és planar, també ho són tots els seus subgrafs: Eliminar vèrtexs i arestes no pot fer que un graf planar deixi de ser-ho. Descrivim un graf no planar minimal com aquell graf el qual tot i no ser planar al eliminar qualsevol vèrtex o aresta, passa a ser-ho. Una altra manera d'entendre el teorema de Wagner per tant és que només hi ha dos grafs no planars minimals; K₅ i K3,3. En certa manera el teorema de Kuratowski forma part del teorema de Wagner, ja que una subdivisó pot ser convertida a un subgraf del mateix tipus al contreure tots els eixos menys un en cada ruta formada pel procés de subdivisió, però en canvi convertir un subgraf a una subdivisió del mateix tipus no sempre és possible. Tot i això, en el cas del dos grafs K₅ i K3,3, és trivial demostrar que almenys un d'aquests dos grafs com a subgraf també en té un d'ells com a subdivisió, per tant tots dos teoremes són equivalents.[10]

El teorema pot ser reformulat d'aquesta manera: tot graf no planar pot ser descompost en peces més simples. Aquesta idea és la precursora del teorema estructural de grafs[11] i el teorema de Robertson-Seymour[12] Anàlegs del teorema de Wagner també són utilitzats en la teoria de matroides.[13]

Criteri de planaritat de Fraysseix-Rosenstiehl

[modifica]
Representació de l'arbre DFS d'un graf
Arbres DFS dels grafs no planars K₅ i K3,3

Es caracteritzen els grafs en termes d'ordenament dreta-esquerra de les arestes en un arbre de cerca en profunditat (Depth-first search).

Donat un graf G, definim un arbre T de cerca de profunditat al dibuixar les arestes trobades quan es descobreix un vèrtex per primera vegada. Això forma un arbre de Trémaux, és a dir, les arestes restants connecten un parell de vèrtexs que estan relacionats entre ells com a ancestre i descendent en T. Per tant, aquestes connexions o frondes no poden entrecreuar diferents branques de l'arbre.

Podem definir cada parell de frondes com T-similars si es troben al mateix costat de la branca, o T-oposades si es troben a costats oposats.

Definim el graf G amb el corresponent arbre de Trémaux T. G és planar si i només si existeix en T un encreuament entre frondes, és a dir, una incompatibilitat entre T-similars i T-oposades dins d'una determinada branca.

Altres criteris

[modifica]
Criteri de planaritat de Whitney:
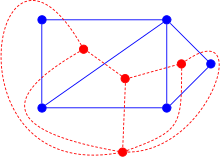
Un graf pla i el seu dual. Cada cicle en el graf blau correspon a un tros minimal en vermell i viceversa, per tant els dos grafs són duals algebraics i tenen matroides duals.

Un graf és planar si i només si el seu graf matroide també és un co-graf (és a dir, és el matroide dual d'un altre graf matroide).

Donat un graf G=(V,E), ha d'existir un altre graf (dual) G'=(V',E') i una correspondència entre les arestes E' i E de tal manera que un subgrup T de E formi un arbre d'expansió de G si i només si les arestes corresponents al subgrup complementari E-T formen un arbre d'expansió de G'. Per tant, G és planar si i només si existeix un graf dual que té un matroide dual al matroide de G. G' també s'anomena el dual algebraic de G, per tant el criteri de Whitney pot ser descrit simplement: Un graf és planar si i només si té un dual algebraic.[14]

Criteri de planaritat de Mac Lane:

Es caracteritzen els grafs per les bases dels seus espais de cicles binaris.

Un graf és pla si i només si el seu espai de cicle té un cicle de base al qual cada aresta del graf participa a com a molt dos vectors base.

Per cada cicle c en un graf G, es pot formar un vector m-dimensional 0-1 que té un 1 a les coordenades de posició corresponents a les arestes en c, i un 0 en la resta de coordenades de posició. L'espai de cicle C(G) del graf és el vector format per totes les combinacions lineals possibles de vectors formades en aquesta via. La 2-base de G és una base de C(G) amb la propietat que, per cada aresta E de G, com a molt dos vectors base tenen coordenades diferents a 0 en la posició corresponent a E. El graf és planar només si té una 2-base.[15]

Teorema de Schnyder:

Es caracteritzen els grafs per la dimensió de Dushnik–Miller d'un ordre parcial associat.

El poset (partially ordered set) d'incidència P(G) d'un graf amb vèrtexs V i arestes E és el poset amb alçada 2 que té V ∪ E com a elements. L'ordre dimensional del poset és el menor nombre possible d'ordenaments als quals la interacció correspon a l'ordre parcial donat.

Un graf és pla si i només si l'ordre dimensional de P(G) és com a molt 3.

Criteri de planaritat de Colin de Verdière:

Utilitza teoria espectral dels grafs per definir un paràmetre μ(G) (Invariant de Colin de Verdière), corresponent al major co-rang possible en una matriu simètrica dels vectors.

Un graf G és pla si i només si μ(G) ≤ 3

Algorismes

[modifica]

Mètode d'addició de rutes

[modifica]

El mètode d'addició de rutes de John Hopcroft i Robert Tarjan va ser el primer a ser publicat (1974) que complia un temps lineal O(n).[16] Actualment hi ha una implementació de l'algorisme publicada a la Llibreria de Dades Eficients i Algorismes (LEDA).[17][18][19]

El 2012, Martyn G. Taylor va generalitzar l'algorisme per generar totes les permutacions d'un ordre cíclic per representacions planes de components biconnectats.[20]

Mètode d'addició de vèrtexs

[modifica]

El mètode d'addició de vèrtexs consisteix en mantenir una estructura de dades representativa de les possibles representacions d'un subgraf induït del graf, i afegint-hi vèrtexs d'un en un. Aquest mètode inicialment (1967) era molt ineficient O(n²), creat per Abraham Lempel i Shimon Even.[21] Va ser millorat més tard per Even i Tarjan, que van trobar una solució amb temps lineal.[22] i per Kellog S. Booth i George S. Lueker, que van desenvolupar l'arbre PQ, una eficient estructura de dades. Gràcies a aquestes millores aquest mètode és més eficient que el d'addició de rutes.[23] Aquest mètode també va ser ampliat per permetre representacions planars en un pla de forma computacionalment eficient.[24] Al 1999, Shih i Hsu van simplificar aquests mètodes utilitzant arbres PC recorregut transversal de l'arbre DPS dels vectors.[25]

Mètode d'addició d'arestes

[modifica]

Al 2004, John Boyer i Wendy Myrvold van desenvolupar un algorisme O(n) simple inspirat en el mètode d'arbre PQ, que utilitza addicions d'arestes per computar una representació planar sempre que sigui possible. En cas contrari, una subdivisió de Kuratowski és computada.[26] Aquest és un dels mètodes més utilitzats avui dia, juntament amb el test de planaritat de Fraysseix, de Mendez i Rosenstiehl.[27][28]). S'han fet comprovacions experimentals amb versions preliminars per comparar-ne l'eficiència.[29] A més, el test de Boyer–Myrvold va ser ampliat per extreure múltiples subdivisions de Kuratowski en temps lineal.[30][31]

Mètode de construcció de seqüències

[modifica]

Aquest mètode utilitza una construcció inductiva de grafs per construir de forma incremental, partint de K₄, representacions planars de cada component de G, i per tant una representació planar del graf.[32] Això permet reduir el test de planaritat a comprovar a cada pas si la següent aresta afegida té els dos extrems a la cara externa de la representació actual. Tot i que la idea és conceptualment simple i funciona a temps lineal, el mètode és complex en trobar la seqüència construïda.

Referències

[modifica]
  1. ↑ Kuratowski, Kazimierz «Sur le problème des courbes gauches en topologie» (en francès). Fund. Math., 15, 1930, p. 271–283.
  2. ↑ Tutte, W. T. «How to draw a graph». Proceedings of the London Mathematical Society, 13, 1963, p. 743–767. DOI: 10.1112/plms/s3-13.1.743.
  3. ↑ Williamson, S. G. «Depth-first search and Kuratowski subgraphs». J. ACM, 31, 4, 9-1984, p. 681–693. DOI: 10.1145/1634.322451.
  4. ↑ Mehlhorn, Kurt; Näher, Stefan. LEDA: A Platform for Combinatorial and Geometric Computing. Cambridge University Press, 1999, p. 510. ISBN 9780521563291. 
  5. ↑ Chimani, Markus; Mutzel, Petra; Schmidt, Jens M. Efficient Extraction of Multiple Kuratowski Subdivisions, 2007, p. 159–170. DOI 10.1007/978-3-540-77537-9_17. 
  6. ↑ Frink, Orrin; Smith, Paul A. «Irreducible non-planar graphs». Bulletin of the AMS, 36, 1930, p. 214.
  7. ↑ Menger, Karl «Über plättbare Dreiergraphen und Potenzen nichtplättbarer Graphen». Anzeiger der Akademie der Wissenschaften in Wien, 67, 1930, p. 85–86.
  8. ↑ Thomassen, Carsten «Kuratowski's theorem». Journal of Graph Theory, 5, 3, 1981, p. 225–241. DOI: 10.1002/jgt.3190050304.
  9. ↑ Wagner, K. «Über eine Eigenschaft der ebenen Komplexe». Math. Ann., 114, 1937, p. 570–590. DOI: 10.1007/BF01594196.
  10. ↑ Bondy, J. A.; Murty, U.S.R.. Graph Theory. 244. Springer, 2008, p. 269. ISBN 9781846289699. 
  11. ↑ Lovász, László «Graph minor theory». Bulletin of the American Mathematical Society, 43, 1, 2006, p. 75–86. DOI: 10.1090/S0273-0979-05-01088-8.
  12. ↑ Chartrand, Gary; Lesniak, Linda; Zhang, Ping. Graphs & Digraphs. 5th. CRC Press, 2010, p. 307. ISBN 9781439826270. 
  13. ↑ Seymour, P. D. «On Tutte's characterization of graphic matroids». Annals of Discrete Mathematics, 8, 1980, p. 83–90. DOI: 10.1016/S0167-5060(08)70855-0.
  14. ↑ Whitney, Hassler «Non-separable and planar graphs». Transactions of the American Mathematical Society, 34, 2, 1932, p. 339–362. DOI: 10.1090/S0002-9947-1932-1501641-2.
  15. ↑ Mac Lane, S. «A combinatorial condition for planar graphs». Fundamenta Mathematicae, 28, 1937, p. 22–32.
  16. ↑ Hopcroft, John; Tarjan, Robert E. «Efficient planarity testing». Journal of the Association for Computing Machinery, 21, 4, 1974, p. 549–568. DOI: 10.1145/321850.321852.
  17. ↑ Mehlhorn, Kurt; Mutzel, Petra «On the Embedding Phase of the Hopcroft and Tarjan Planarity Testing Algorithm». Algorithmica, 16, 2, 1996, p. 233–242. DOI: 10.1007/bf01940648.
  18. ↑ Mehlhorn, Kurt; Mutzel, Petra; Näher, Stefan. An Implementation of the Hopcroft and Tarjan Planarity Test and Embedding Algorithm, 1993. 
  19. ↑ Mehlhorn, Kurt; Näher, Stefan «LEDA: A library of efficient data types and algorithms». Communications of the ACM, 38, 1, 1995, p. 96–102. DOI: 10.1145/204865.204889.
  20. ↑ Martyn G. Taylor. «Planarity Testing by Path Addition» University of Kent; Tesi (Ph.D), 2012. Arxivat de l'original el 2 de febrer de 2014.
  21. ↑ Lempel, A.; Even, S. Theory of Graphs. Nova York: Gordon and Breach, 1967, p. 215-232. «An algorithm for planarity testing of graphs» 
  22. ↑ Even, Shimon; Tarjan, Robert E. «Computing an st-numbering». Theoretical Computer Science, 2, 3, 1976, p. 339–344. DOI: 10.1016/0304-3975(76)90086-4.
  23. ↑ Boyer & Myrvold (2004), p. 243: “Its implementation in LEDA is slower than LEDA implementations of many other O(n)-time planarity algorithms.”
  24. ↑ Chiba, N.; Nishizeki, T.; Abe, A.; Ozawa, T. «A linear algorithm for embedding planar graphs using PQ–trees». Journal of Computer and System Sciences, 30, 1, 1985, p. 54–76. DOI: 10.1016/0022-0000(85)90004-2.
  25. ↑ Shih, W. K.; Hsu, W. L. «A new planarity test». Theoretical Computer Science, 223, 1–2, 1999, p. 179–191. DOI: 10.1016/S0304-3975(98)00120-0.
  26. ↑ Boyer, John M.; Myrvold, Wendy J. «On the cutting edge: simplified O(n) planarity by edge addition». Journal of Graph Algorithms and Applications, 8, 3, 2004, p. 241–273. DOI: 10.7155/jgaa.00091.
  27. ↑ de Fraysseix, H.; Ossona de Mendez, P.; Rosenstiehl, P. «Trémaux Trees and Planarity». International Journal of Foundations of Computer Science, 17, 5, 2006, p. 1017–1030. DOI: 10.1142/S0129054106004248.
  28. ↑ Brandes, Ulrik. The left-right planarity test, 2009. 
  29. ↑ Boyer, John M.; Cortese, P. F.; Patrignani, M.; Battista, G. D.. Proc. 11th Int. Symp. Graph Drawing (GD '03). 2912. Springer-Verlag, 2003, p. 25–36. «Stop minding your P's and Q's: implementing a fast and simple DFS-based planarity testing and embedding algorithm» 
  30. ↑ Chimani, M.; Mutzel, P.; Schmidt, J. M.. Proc. 15th Int. Symp. Graph Drawing (GD'07). 4875. Sydney, Australia: Springer-Verlag, 2008, p. 159–170. «Efficient extraction of multiple Kuratowski subdivisions» 
  31. ↑ Williamson, S. G. «Depth First Search and Kuratowski Subgraphs». Journal of the ACM, 31, 4, 1984, p. 681–693. DOI: 10.1145/1634.322451.
  32. ↑ Schmidt, Jens M. Automata, Languages, and Programming. 8572, 2014, p. 967–978. DOI 10.1007/978-3-662-43948-7_80. ISBN 978-3-662-43947-0. 

Enllaços externs

[modifica]
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Test_de_planaritat&oldid=34379596»