Mètodes numèrics per a equacions diferencials ordinàries

Els mètodes numèrics per a equacions diferencials ordinàries són mètodes utilitzats per trobar aproximacions numèriques a les solucions d'equacions diferencials ordinàries (ODE). El seu ús també es coneix com "integració numèrica", encara que aquest terme també pot referir-se al càlcul d'integrals.

Il·lustració d'integració numèrica per a l'equació diferencial $y'=y,y(0)=1.$ La mida del pas és $h=1.0$ .

Moltes equacions diferencials no es poden resoldre amb exactitud. Amb finalitats pràctiques, però - com en enginyeria – Sovint n'hi ha prou amb una aproximació numèrica de la solució. Els algorismes estudiats aquí es poden utilitzar per calcular aquesta aproximació. Un mètode alternatiu és utilitzar tècniques de càlcul per obtenir una expansió en sèrie de la solució.

La mateixa il·lustració per $h=0.25.$ El mètode del punt mitjà convergeix més ràpidament que el mètode d'Euler, com $h\to 0$ .

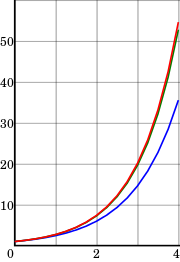
Les equacions diferencials ordinàries es produeixen en moltes disciplines científiques, com ara la física, la química, la biologia i l'economia. A més, alguns mètodes en equacions diferencials parcials numèriques converteixen l'equació diferencial parcial en una equació diferencial ordinària, que després s'ha de resoldre.

El problema

Una equació diferencial de primer ordre és un problema de valor inicial (IVP) de la forma,

$y'(t)=f(t,y(t)),\qquad y(t_{0})=y_{0},$

(1)

on $f$ és una funció $f:[t_{0},\infty )\times \mathbb {R} ^{d}\to \mathbb {R} ^{d}$, i la condició inicial $y_{0}\in \mathbb {R} ^{d}$ és un vector donat. De primer ordre significa que només la primera derivada de y apareix a l'equació i les derivades superiors estan absents.

Sense perdre la generalitat dels sistemes de primer ordre, ens limitem a les equacions diferencials de primer ordre, perquè una EDO d'ordre superior es pot convertir en un sistema més gran d'equacions de primer ordre introduint variables addicionals. Per exemple, l'equació de segon ordre y′′ = −y es pot reescriure com a dues equacions de primer ordre: y′ = z i z′ = −y.

En aquesta secció, descrivim mètodes numèrics per a IVP i observem que els problemes de valor de límit (BVP) requereixen un conjunt diferent d'eines. En una BVP, es defineixen valors o components de la solució y en més d'un punt. Per això, cal utilitzar diferents mètodes per resoldre els BVP. Per exemple, el mètode de tir (i les seves variants) o els mètodes globals com les diferències finites, els mètodes de Galerkin, o els mètodes de col·locació són adequats per a aquesta classe de problemes.

El teorema de Picard–Lindelöf estableix que hi ha una solució única, sempre que f sigui contínua de Lipschitz.

Mètodes

Els mètodes numèrics per resoldre IVP de primer ordre sovint es troben en una d'aquestes dues grans categories: mètodes lineals de passos múltiples o mètodes Runge-Kutta. Es pot realitzar una altra divisió dividint els mètodes en els que són explícits i els que són implícits. Per exemple, els mètodes multistep lineals implícits inclouen els mètodes Adams-Moulton i els mètodes de diferenciació cap enrere (BDF), mentre que els mètodes Runge-Kutta implícits inclouen Runge-Kutta (DIRK) implícit en diagonal, Runge implícit en diagonal individualment. –Kutta (SDIRK), i Gauss–Radau (basat en quadratura gaussiana) mètodes numèrics. Els exemples explícits de la família lineal de passos múltiples inclouen els mètodes Adams–Bashforth, i qualsevol mètode Runge–Kutta amb una taula de Butcher en diagonal inferior és explícit. Una regla general fluixa dicta que les equacions diferencials rígides requereixen l'ús d'esquemes implícits, mentre que els problemes no rígids es poden resoldre de manera més eficient amb esquemes explícits.

Els anomenats mètodes lineals generals (GLM) són una generalització de les dues grans classes de mètodes anteriors.