Nombre surreal
En matemàtiques, el sistema de nombres surreals és una classe pròpia totalment ordenada que conté els nombres reals, així com nombres infinits i infinitesimals, més grans o més petits respectivament en valor absolut que qualsevol nombre real positiu. Els surreals comparteixen moltes propietats amb els reals, incloses les operacions aritmètiques habituals (suma, resta, multiplicació i divisió); com a tal, formen un cos ordenat.[Nota 1]
-
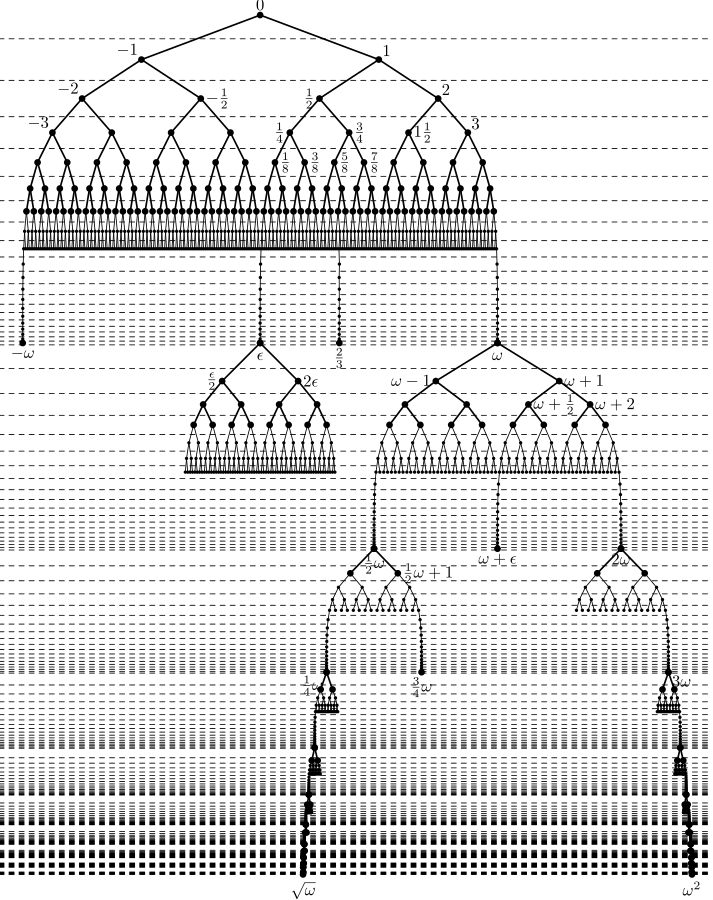
Una visualització de l'arbre de nombres surreals
Si es formulen a la teoria de conjunts de von Neumann-Bernays-Gödel, els nombres surreals són un camp ordenat universal en el sentit que tots els altres camps ordenats, com ara els racionals, els reals, les funcions racionals, el camp de Levi-Civita, els nombres superreals (inclosos els nombres hiperreals) es poden realitzar com a subcamps dels surreals.[1]
Els nombres surreals també contenen tots els nombres ordinals transfinits; l'aritmètica sobre ells ve donada per les operacions naturals. També s'ha demostrat (a la teoria de conjunts de von Neumann-Bernays-Gödel) que el camp hiperreal de classe màxima és isomorf al camp surreal de classe màxima.
Història del concepte
[modifica]La investigació sobre el final del joc del Go de John Horton Conway va conduir a la definició i construcció originals dels nombres surreals.[2] La construcció de Conway es va introduir al llibre de 1974 de Donald Knuth, Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics i Found Total Happiness. En el seu llibre, que pren la forma d'un diàleg, Knuth va encunyar el terme «nombres surreals» per al que Conway havia anomenat simplement «nombres».[3] Conway va adoptar més tard el terme de Knuth i va utilitzar els surreals per analitzar els jocs al seu llibre de 1976 On Numbers and Games.
Una ruta separada per definir els surreals va començar el 1907, quan Hans Hahn va introduir les sèries de Hahn com a generalització de les sèries de potències formal, i Felix Hausdorff va introduir certs conjunts ordenats anomenats conjunts ηα per als ordinals α i va preguntar si era possible trobar un grup ordenat compatible o una estructura de camp. El 1962 Norman Alling va utilitzar una forma modificada de sèries de Hahn per construir aquests camps ordenats associats a determinats ordinals α, i el 1987 va demostrar que si es pren α la classe de tots els ordinals en la construcció, s'obté una classe que és un camp ordenat isomòrfic als nombres surreals.[4]
Si els surreals es consideren «només» un camp tancat real de mida de classe adequada, l'article d'Alling de 1962[4] tracta el cas dels cardinals fortament inaccessibles que naturalment es poden considerar classes adequades que tallen la jerarquia acumulada de l'univers una etapa per sobre del cardinal. Alling, per tant, mereix molt de crèdit pel descobriment o invenció dels nombres surreals en aquest sentit. Tanmateix, hi ha una important estructura de camp addicional sobre els nombres surreals que no és visible a través d'aquesta lent, és a dir, la noció d'«aniversari» i la corresponent descripció natural dels surreals com a resultat d'un procés d'ompliment de talls al llarg dels seus aniversaris donat per Conway. Aquesta estructura addicional s'ha convertit en fonamental per a una comprensió moderna dels nombres surreals i, per tant, se li dona crèdit a Conway per haver descobert els surreals tal com els coneixem avui: el mateix Alling li dona tot el crèdit a Conway en un article de 1985 que precedeix el seu llibre sobre el tema.[5]
Descripció
[modifica]En la construcció de Conway,[6] els nombres surreals es construeixen per etapes, juntament amb un ordre ≤ tal que per a dos nombres surreals qualsevol a i b, a ≤ b o b ≤ a (tots dos es poden mantenir, en aquest cas a i b són equivalents i denoten el mateix nombre). Cada nombre es forma a partir d'un parell ordenat de subconjunts de nombres ja construïts: donats subconjunts L i R de nombres de manera que tots els membres de L siguin estrictament menors que tots els membres de R, llavors el parell {L | R} representa un nombre de valor intermedi entre tots els membres de L i tots els membres de R.
Diferents subconjunts poden acabar definint el mateix nombre: {L | R } i {L′ | R′} pot definir el mateix nombre encara que L ≠ L′ i R ≠ R′; Un fenomen similar es produeix quan els nombres racionals es defineixen com a quocients de nombres enters: 12 i 24 són representacions diferents del mateix nombre racional. En sentit estricte, els nombres surreals són classes d'equivalència de representacions de forma {L | R} que designen el mateix nombre.
En la primera etapa de construcció, no hi ha números existents prèviament, per la qual cosa l'única representació ha d'utilitzar el conjunt buit: { | }. Aquesta representació, on en els llocs de L i R estan buits, s'anomena 0.
- { | } = 0
Les etapes posteriors donen formes com ara
- { 0 | } = 1
- { 1 | } = 2
- { 2 | } = 3
i
- { | 0 } = −1
- { | −1 } = −2
- { | −2 } = −3
Així, els nombres enters estan continguts dins dels nombres surreals; les identitats anteriors són definicions, en el sentit que el costat dret és un nom per al costat esquerre. Que els noms són realment adequats serà evident quan es defineixin les operacions aritmètiques sobre nombres surreals, com a la secció següent.
De la mateixa manera, representacions com
- { 0 | 1 } = 12
- { 0 | 12 } = 14
- { 12 | 1 } = 34
sorgeixen, de manera que els racionals diàdics (nombres racionals els denominadors dels quals són potències de 2) estan continguts dins dels nombres surreals.
Després d'un nombre infinit d'etapes, es fan disponibles infinits subconjunts, de manera que qualsevol nombre real a es pot representar per { La | Ra }, on La és el conjunt de tots els racionals diàdics menors que a i Ra és el conjunt de tots els racionals diàdics majors que a (que recorda un tall de Dedekind). Així, els nombres reals també estan inclosos dins dels surreals.
També hi ha representacions com
- { 0, 1, 2, 3, ... | } = ω
- { 0 | 1, 12, 14, 18, ... } = ε
on ω és un nombre transfinit més gran que tots els nombres enters i ε és un infinitesimal major que 0 però menor que qualsevol nombre real positiu. A més, les operacions aritmètiques estàndard (suma, resta, multiplicació i divisió) es poden estendre a aquests nombres no reals d'una manera que converteix la col·lecció de nombres surreals en un camp ordenat, de manera que es pot parlar de 2ω o ω − 1 i així successivament.
Construcció
[modifica]Els nombres surreals es construeixen de manera inductiva com a classes d'equivalència de parells de conjunts de nombres surreals, restringides per la condició que cada element del primer conjunt sigui més petit que cada element del segon conjunt. La construcció consta de tres parts interdependents:
- la regla de construcció,
- la regla de comparació, i
- la regla d'equivalència.
Forma, conjunt esquerre i conjunt dret
[modifica]Una «forma» és un parell de conjunts de nombres surreals, anomenats «conjunt esquerre» i «conjunt dret». Una forma amb el conjunt esquerre L i el conjunt dret R s'escriu { L | R }. Quan L i R es donen com a llistes d'elements, s'ometen les claus que els envolten.
Un dels dos conjunts (esquerre o dret) d'una formulari pot ser el conjunt buit. La forma { { } | { } } (amb els conjunts esquerra dreta buits) també s'escriu { | }.
Formes numèriques i les seves classes equivalents
[modifica]- Regla de construcció: Una forma { L | R } és numèrica si la intersecció de L i R és el conjunt buit i cada element de R és més gran que cada element de L, segons la relació d'ordre ≤ donada per la regla de comparació següent.
- Regla de comparació: Les formes numèriques es col·loquen en classes d'equivalència; cada classe d'equivalència és un «nombre surreal». Els elements del conjunt esquerre i dret d'una forma s'extreuen de l'univers dels nombres surreals (no de «formes», sinó de les seves «classes d'equivalència»).
- Regla d'equivalència: Dues formes numèriques x i y són formes del mateix nombre (es troben a la mateixa classe d'equivalència) si i només si x ≤ y i y ≤ x.
Una relació d'ordenació ha de ser antisimètrica, és a dir, ha de tenir la propietat que x = y (és a dir, x ≤ y i y ≤ x són certes) només quan x i y són el mateix objecte. Aquest no és el cas de les formes dels nombres surreals, però és cert per construcció de nombres surreals (classes d'equivalència).
La classe d'equivalència que conté { | } està etiquetat com 0; en altres paraules, { | } és una forma del nombre surreal 0.
Ordre
[modifica]La definició recursiva dels nombres surreals es completa definint la comparació:
.
Els nombres surreals es poden comparar entre si (o amb formes numèriques) escollint una forma numèrica de la seva classe d'equivalència per representar cada nombre surreal.
Inducció
[modifica]Aquest grup de definicions és recursiu, i requereix alguna forma d'inducció matemàtica per definir l'univers dels objectes (formes i nombres) que hi apareixen. Els únics nombres surreals als quals es pot arribar mitjançant la inducció finita són les fraccions diàdiques; es pot arribar a un univers més ampli donada alguna forma d'inducció transfinita.
Regla d'inducció
[modifica]- Hi ha una generació S0 = { 0 }, en la qual 0 consta de la forma única { | }.
- Donat qualsevol nombre ordinal n, la generació Sn és el conjunt de tots els nombres surreals que es generen per la regla de construcció a partir de subconjunts de
El cas base és en realitat un cas especial de la regla d'inducció, amb 0 considerat com a etiqueta per al «mínim ordinal». Com que no existeix Si amb i < 0, l'expressió és el conjunt buit; l'únic subconjunt del conjunt buit és el conjunt buit i, per tant, S0 consta d'una única forma surreal, { | }, que es troba en una única classe d'equivalència 0.
Per a cada nombre ordinal finit n, Sn està ben ordenat per l'ordenació induïda per la regla de comparació dels nombres surreals.
La primera iteració de la regla d'inducció produeix les tres formes numèriques { | 0 } < { | } < { 0 | } (la forma { 0 | 0 } no és numèrica perquè 0≤0). La classe d'equivalència que conté { 0 | } s'etiqueta 1 i la classe d'equivalència conté { | 0 } s'etiqueta −1. Aquestes tres etiquetes tenen un significat especial en els axiomes que defineixen un anell; són la identitat additiva (0), la identitat multiplicativa (1) i la inversa additiva d'1 (−1). Les operacions aritmètiques definides a continuació són coherents amb aquestes etiquetes.
Per a cada i < n, ja que tota forma vàlida en Si també és una forma vàlida en Sn, tots els nombres en Si també apareixen a Sn (com a superconjunts de la seva representació en Si); l'expressió d'unió de conjunt apareix a la nostra regla de construcció, en lloc de la forma més simple Sn−1, de manera que la definició també té sentit quan n és un ordinal límit. Es diu que els nombres en Sn són un superconjunt d'algun nombre en Si si han estat «heretats» de la generació i. El valor més petit d'α per al qual apareix un nombre surreal donat a Sα s'anomena el seu «aniversari». Per exemple, l'aniversari de 0 és 0, i l'aniversari de −1 és 1.
Una segona iteració de la regla de construcció produeix l'ordenació següent de les classes d'equivalència:
- { | −1 } = { | −1, 0 } = { | −1, 1 } = { | −1, 0, 1 }
- < { | 0 } = { | 0, 1 }
- < { −1 | 0 } = { −1 | 0, 1 }
- < { | } = { −1 | } = { | 1 } = { −1 | 1 }
- < { 0 | 1 } = { −1, 0 | 1 }
- < { 0 | } = { −1, 0 | }
- < { 1 | } = { 0, 1 | } = { −1, 1 | } = { −1, 0, 1 | }
La comparació d'aquestes classes d'equivalència és coherent, independentment de l'elecció de la forma. Segueixen tres observacions:
- S₂ conté quatre nous nombres surreals. Dos contenen formes extremes: { | −1, 0, 1 } conté tots els nombres de generacions anteriors en el seu conjunt dret, i { −1, 0, 1 | } conté tots els números de generacions anteriors al seu conjunt esquerre. Els altres tenen una forma que divideix tots els números de generacions anteriors en dos conjunts no buits.
- Cada nombre surreal x que existia a la «generació» anterior també existeix en aquesta generació, i inclou almenys una forma nova: una partició de tots els nombres diferents de x de generacions anteriors en un conjunt esquerre (tots els nombres inferiors a x) i un conjunt dret (tots els nombres majors que x).
- La classe d'equivalència d'un nombre depèn només de l'element màxim del seu conjunt esquerre i de l'element mínim del conjunt dret.
Les interpretacions informals de { 1 | } i { | −1 } són «el nombre just després d'1» i «el nombre just abans de -1» respectivament; les seves classes d'equivalència s'anomenen 2 i −2. Les interpretacions informals de { 0 | 1 } i { −1 | 0 } són «el nombre a mig camí entre 0 i 1» i «el nombre a mig camí entre −1 i 0» respectivament; les seves classes d'equivalència estan etiquetades 12 i −12. Aquestes etiquetes també estaran justificades per les regles per a la suma i la multiplicació surreal que s'explica a continuació.
Les classes d'equivalència a cada etapa n d'inducció es poden caracteritzar per les seves «n-formes» completes (cadascun conté tants elements com sigui possible de generacions anteriors en els seus conjunts esquerre i dret). O bé aquesta forma completa conté tots els nombres de generacions anteriors en el seu conjunt esquerre o dret (en aquest cas aquesta és la primera generació en què apareix aquest nombre), o conté tots els números de generacions anteriors menys un (en aquest cas és una forma nova d'aquest número). Conservem les etiquetes de la generació anterior per a aquests números «antics» i escrivim l'ordre anterior utilitzant les etiquetes antigues i noves:
- −2 < −1 < −12 < 0 < 12 < 1 < 2.
La tercera observació s'estén a tots els nombres surreals amb conjunts esquerra i dreta finits; per a conjunts infinits d'esquerra o dreta, això és vàlid en una forma alterada, ja que els conjunts infinits poden no contenir un element màxim o mínim. El nombre { 1, 2 | 5, 8 } és, per tant, equivalent a { 2 | 5}; es pot establir que es tracta de formes de 3 utilitzant la propietat de l'aniversari, que és una conseqüència de les regles anteriors.
Propietat de l'aniversari
[modifica]Una forma x = { L | R } que es produeix a la generació n representa un nombre heretat d'una generació anterior i < n si i només si hi ha algun nombre en Si que sigui més gran que tots els elements de L i menor que tots els elements de la R; en altres paraules, si L i R ja estan separats per un nombre creat en una etapa anterior, aleshores x no representa un nombre nou sinó un ja construït.
Si x representa un nombre de qualsevol generació anterior a n, hi ha almenys aquesta generació i, i exactament un número c amb aquest mínim i com a aniversari que es troba entre L i R; x és una forma d'aquesta c. En altres paraules, es troba en la classe d'equivalència en Sn que és un superconjunt de la representació de c en la generació i.
Aritmètica
[modifica]La suma, la negació (addició inversa) i la multiplicació de les formes de nombres surreals x = { XL | XR } i y = { YL | YR } es defineixen per tres fórmules recursives.
Negació
[modifica]Negació d'un nombre donat x = { XL | XR } és definit per:
- ,
on la negació d'un conjunt S de nombres ve donada pel conjunt dels elements negats de S:
- .
Aquesta fórmula implica la negació dels nombres surreals que apareixen en els conjunts esquerre i dret de x, que s'ha d'entendre com el resultat d'escollir una forma del nombre, avaluar la negació d'aquesta forma i prendre la classe d'equivalència de la forma resultant. Això només té sentit si el resultat és el mateix, independentment de l'elecció de la forma de l'operand. Això es pot demostrar de manera inductiva utilitzant el fet que els nombres que apareixen a XL i XR s'extreuen de generacions anteriors a aquella en què apareix la forma x per primera vegada, i observant el cas especial:
- .
Addicció
[modifica]La definició d'addició també és una fórmula recursiva:
- ,
on
- .
Aquesta fórmula implica sumes d'un dels operands originals i un nombre surreal extret del conjunt esquerre o dret de l'altre. Es pot demostrar inductivament amb els casos especials:
- 0 + 0 = { | } + { | } = { | } = 0
- x + 0 = x + { | } = { XL + 0 | XR + 0 } = { XL | XR } = x
- 0 + y = { | } + y = { 0 + YL | 0 + YR } = { YL | YR } = y
Per exemple :
- 12 + 12 = { 0 | 1 } + { 0 | 1 } = { 0 + 12, 12 + 0 | 1 + 12, 12 + 1} = { 12 | 32 },
que per la propietat d'aniversari és una forma d'1. Això justifica l'etiqueta utilitzada a l'apartat anterior.
Multiplicació
[modifica]La multiplicació també es pot definir recursivament, començant pels casos especials que involucren 0, la identitat multiplicativa 1 i la seva addició inversa -1:
La fórmula conté expressions aritmètiques que impliquen els operands i els seus conjunts esquerre i dret, com ara l'expressió que apareix al conjunt esquerre del producte de x i y. S'entén com el conjunt de números generats escollint totes les combinacions possibles de membres de i , i substituint-los a l'expressió.
Per exemple, per demostrar que el quadrat de 12 és 14:
Divisió
[modifica]La definició de divisió es fa en termes de recíproc i multiplicació:
on[7]
per a y positiu. Només es permet yL positiu a la fórmula, sense tenir en compte els termes no positius (i yR sempre són positius). Aquesta fórmula implica no només recursivitat en termes de poder dividir per nombres dels conjunts esquerre i dret de y, sinó també recursivitat en què els membres dels conjunts esquerre i dret del mateix 1y . 0 sempre és un membre del conjunt esquerre de 1y, i això es pot utilitzar per trobar més termes de manera recursiva. Per exemple, si y = 3 = { 2 | }, llavors coneixem un terme esquerre de 13 serà 0. Això al seu torn significa que 1+(2−3)02 = 12 és un terme correcte. Això vol dir:
és un terme esquerre. Això vol dir
serà un terme correcte. Continuant, això dona
Per a y negatiu, 1y és equivalent a
Si y = 0, llavors 1y es indefinit.
Consistència
[modifica]Es pot demostrar que les definicions de negació, suma i multiplicació són coherents, en el sentit que:
- L'addició i la negació es defineixen recursivament en termes de passos d'addició i negació «més simples», de manera que les operacions sobre nombres amb aniversari n eventualment s'expressaran completament en termes d'operacions sobre nombres amb aniversaris inferiors a n;
- La multiplicació es defineix recursivament en termes d'addicions, negacions i passos de multiplicació «més simples», de manera que el producte dels nombres amb aniversari n s'expressarà completament en termes de sumes i diferències de productes de nombres amb aniversaris inferiors a n;
- Sempre que els operands siguin formes de nombres surreals ben definides (cada element del conjunt esquerre és menor que cada element del conjunt dret), els resultats tornen a ser formes de nombres surreals ben definides;
- Les operacions es poden estendre als nombres (classes d'equivalència de formes): el resultat de negar x o sumar o multiplicar x i y representarà el mateix nombre independentment de l'elecció de la forma de x i y; i
- Aquestes operacions obeeixen als axiomes d'associativitat, commutativitat, inversa additiva i distributivitat en la definició d'un camp, amb identitat additiva 0 = { | } i identitat multiplicativa 1 = { 0 | }.
Amb aquestes regles ara es pot comprovar que els números trobats en les primeres generacions estaven correctament etiquetats. La regla de construcció es repeteix per obtenir més generacions de surreals:
- S0 = { 0 }
- S1 = { −1 < 0 < 1 }
- S₂ = { −2 < −1 < −12 < 0 < 12 < 1 < 2}
- S₃ = { −3 < −2 < −32 < −1 < −34 < −12 < −14 < 0 < 14 < 12 < 34 < 1 < 32 < 2 < 3 }
- S4 = { −4 < −3 < ... < −18 < 0 < 18 < 14 < 38 < 12 < 58 < 34 < 78 < 1 < 54 < 32 < 74 < 2 < 52 < 3 < 4 }
Tancament aritmètic
[modifica]Per a cada nombre natural (ordinal finit) n, tots els nombres generats en Sn són fraccions diàdiques, és a dir, es poden escriure com una fracció irreductible a2b, on a i b són nombres enters i 0 ≤ b < n.
El conjunt de tots els nombres surreals que es generen en alguns per a n finit es pot denotar com S∗ = . Es poden formar les tres classes
dels quals S∗ és la unió. Cap individu Sn està tancat sota la suma i la multiplicació (excepte S0), però S∗ ho és; és el subanell dels racionals format per totes les fraccions diàdiques.
Hi ha infinits nombres ordinals β per als quals el conjunt de nombres surreals amb aniversari inferior a β es tanca sota les diferents operacions aritmètiques.[8] Per a qualsevol ordinal α, el conjunt de nombres surreals amb aniversari inferior a β = ωα (utilitzant potències de ω) es tanca sota la suma i forma un grup;[Nota 2] per als aniversaris inferiors a ωωα es tanca sota la multiplicació i forma un anell; i per a l'aniversari inferior a un nombre èpsilon εα (ordinal) es tanca sota invers multiplicatiu i forma un camp. Aquests darrers conjunts també estan tancats sota la funció exponencial definida per Kruskal i Gonshor.[8][9]
Tanmateix, sempre és possible construir un nombre surreal que sigui més gran que qualsevol membre d'un conjunt de surreals (incloent el conjunt del costat esquerre del constructor) i, per tant, la col·lecció de nombres surreals és una classe adequada. Amb la seva ordenació i operacions algebraiques constitueixen un camp ordenat, amb l'advertència que no formen un conjunt. De fet, és el camp ordenat més gran, ja que cada camp ordenat és un subcamp dels nombres surreals.[1] La classe de tots els nombres surreals es denota amb el símbol .
Infinit
[modifica]Definim Sω com el conjunt de tots els nombres surreals generats per la regla de construcció a partir de subconjunts de S∗ (aquest és el mateix pas inductiu que abans, ja que el nombre ordinal ω és l'ordinal més petit que és més gran que tots els nombres naturals; tanmateix, la unió de conjunts que apareix en el pas inductiu és ara una unió infinita de conjunts finits i, per tant, aquest pas només es pot realitzar en una teoria de conjunts que permeti aquesta unió.) Un nombre positiu únic infinitament gran es produeix a Sω:
Sω també conté objectes que es poden identificar com a nombres racionals. Per exemple, la forma ω-completa de la fracció 13 ve donada per:
- .
El producte d'aquesta forma de 13 amb qualsevol forma de 3 és una forma el conjunt esquerre de la qual només conté nombres inferiors a 1 i el conjunt dret de la qual només conté nombres superiors a 1; la propietat d'aniversari implica que aquest producte és una forma d'1.
No només apareixen a Sω la resta de nombres racionals; la resta de nombres reals finits també ho fan. Per exemple,
- .
Els únics infinits en Sω són ω i −ω; però hi ha altres nombres no reals en Sω entre els reals. Considerem el nombre positiu més petit de Sω:
- .
Aquest nombre és més gran que zero però menor que totes les fraccions diàdiques positives. Per tant, és un nombre infinitesimal, sovint etiquetat com ε. La forma ω-completa de ε (respectivament -ε) és la mateixa que la forma ω-completa de 0, excepte que 0 s'inclou al conjunt esquerre (respectivament dret). Els únics infinitesimals «purs» en Sω són ε i la seva inversa additiva -ε; sumant-los a qualsevol fracció diàdica y es produeixen els nombres y ± ε, que també es troben en Sω.
Es pot determinar la relació entre ω i ε multiplicant-ne formes particulars per obtenir:
- ω · ε = { ε · S+ | ω · S+ + S∗ + ε · S∗ }.
Aquesta expressió només està ben definida en una teoria de conjunts que permet la inducció transfinita fins a Sω2. En aquest sistema, es pot demostrar que tots els elements del conjunt esquerre de ωSω·Sωε són infinitesimals positius i tots els elements del conjunt dret són infinits positius i, per tant, ωSω·Sωε és el nombre finit positiu més antic, 1. En conseqüència, 1ε = ω. Alguns autors utilitzen sistemàticament ω−1 en lloc del símbol ε.
Continguts de Sω
[modifica]Donat qualsevol x = { L | R } a Sω, és exactament cert un dels següents:
- L i R són tots dos buits, en aquest cas x = 0;
- R és buit i algun nombre enter n≥0 és més gran que tots els elements de L, en aquest cas x és igual al nombre enter més petit n;
- R és buit i cap nombre enter n és més gran que tots els elements de L, en aquest cas x és igual a +ω;
- L és buit i algun nombre enter n≤0 és menor que tots els elements de R, en aquest cas x és igual al nombre enter més gran n;
- L és buit i cap nombre enter n és menor que tots els elements de R, en aquest cas x és igual a −ω;
- L i R no són buits i:
- Alguna fracció diàdica y està «estrictament entre» L i R (més gran que tots els elements de L i menor que tots els elements de R), en aquest cas x és igual a la fracció diàdica y més antiga;
- Cap fracció diàdica y es troba estrictament entre L i R, sinó alguna fracció diàdica és més gran o igual que tots els elements de L i menor que tots els elements de R, en aquest cas x és igual a y + ε;
- Cap fracció diàdica y es troba estrictament entre L i R, sinó alguna fracció diàdica és més gran que tots els elements de L i menor o igual que tots els elements de R, en aquest cas x és igual a y − ε;
- Cada fracció diàdica és més gran que algun element de R o menor que algun element de L, en aquest cas x és un nombre real que no té representació com a fracció diàdica.
Sω no és un camp algebraic, perquè no està tancat sota operacions aritmètiques; considerem ω+1, la forma del qual
no es troba en cap nombre de Sω. El subconjunt màxim de Sω que es tanca sota (una sèrie finita de) operacions aritmètiques és el camp dels nombres reals, obtingut deixant de banda els infinits ±ω, els infinitesimals ±ε i els infinitesimals veïns y ± ε de cada fracció diàdica diferent de zero y.
Aquesta construcció dels nombres reals difereix dels talls de Dedekind de l'anàlisi estàndard perquè parteix de fraccions diàdiques en lloc de racionals generals i identifica naturalment cada fracció diàdica en Sω amb les seves formes en generacions anteriors (les formes ω-completes dels elements reals de Sω estan en correspondència un a un amb els reals obtinguts per talls de Dedekind, amb la condició que els reals de Dedekind corresponents a nombres racionals es representin per la forma en què el punt de tall s'omet de tant conjunts esquerre com dret). Els racionals no són una etapa identificable en la construcció surreal; són només el subconjunt de Sω que conté tots els elements x tals que x b = a per a alguns a i alguns b diferents de zero, tots dos extrets de S∗. En demostrar que està tancat sota repeticions individuals de les operacions aritmètiques surreals, es pot demostrar que és un cos; i mostrant que cada element de és accessible des de S∗ mitjançant una sèrie finita (no més llarga de dues, en realitat) d'operacions aritmètiques que inclouen la inversió multiplicativa, es pot demostrar que és estrictament més petit que el subconjunt de Sω identificat amb els reals.
El conjunt Sω té la mateixa cardinalitat que els nombres reals . Això es pot demostrar mostrant mapes exhaustius de Sω a l'interval unitari tancat I de i viceversa. Assignar Sω a I és una rutina; mapejar nombres inferiors o iguals a ε (incloent −ω) a 0, nombres majors o iguals a 1 − ε (incloent ω) a 1 i nombres entre ε i 1 − ε al seu equivalent a I (mapejar els veïns infinitesimals y±ε de cada fracció diàdica y, juntament amb la mateixa y, a y). Per mapejar I a Sω, s'ha de mapejar el terç central (obert) (13, 23) de I a { | } = 0; el terç central (79, 89) del terç superior a { 0 | } = 1; i així successivament. Això mapeja un interval obert no buit de I a cada element de S∗, monòtonament. El residu de I consisteix en el conjunt de Cantor 2ω, cada punt del qual s'identifica de manera única mitjançant una partició dels intervals del terç central en conjunts esquerre i dret, corresponents precisament a una forma { L | R } en Sω. Això situa el conjunt de Cantor en correspondència un a un amb el conjunt de nombres surreals amb aniversari ω.
Inducció transinfinita
[modifica]Continuar realitzant la inducció transfinita més enllà de Sω produeix més nombres ordinals α, cadascun representat com el nombre surreal més gran amb aniversari α (aquesta és essencialment una definició dels nombres ordinals resultants de la inducció transfinita). El primer d'aquests ordinals és ω+1 = { ω | }. Hi ha un altre nombre infinit positiu a la generació ω+1:
- ω − 1 = { 1, 2, 3, 4, ... | ω }.
El nombre surreal ω − 1 no és un ordinal; l'ordinal ω no és el successor de cap ordinal. Aquest és un nombre surreal amb aniversari ω+1, que s'etiqueta ω − 1 perquè coincideix amb la suma de ω = { 1, 2, 3, 4, ... | } i −1 = { | 0}. De la mateixa manera, hi ha dos nous nombres infinitesimals a la generació ω + 1:
- 2ε = ε + ε = { ε | 1 + ε, 12 + ε, 14 + ε, 18 + ε, ... } i
- ε2 = ε · 12 = { 0 | ε }.
En una etapa posterior de la inducció transfinita, hi ha un nombre més gran que ω + k per a tots els nombres naturals k:
- 2ω = ω + ω = { ω+1, ω+2, ω+3, ω+4, ... | }
Aquest nombre es pot anomenar ω + ω tant perquè el seu aniversari és ω + ω (el primer nombre ordinal no accessible des de ω per l'operació successora) perquè coincideix amb la suma surreal de ω i ω; també es pot etiquetar 2ω perquè coincideix amb el producte de ω = { 1, 2, 3, 4, ... | } i 2 = { 1 | }. És l'ordinal del segon límit; arribar-hi des de ω mitjançant el pas de construcció requereix una inducció transfinita
Això implica una unió infinita de conjunts infinits, que és una operació teòrica de conjunts «més forta» que la inducció transfinita anterior requerida.
S'ha de tenir en compte que la suma i la multiplicació convencionals d'ordinals no sempre coincideixen amb aquestes operacions sobre les seves representacions surreals. La suma dels ordinals 1 + ω és igual a ω, però la suma surreal és commutativa i produeix 1 + ω = ω + 1 > ω. La suma i la multiplicació dels nombres surreals associats als ordinals coincideix amb la suma natural i el producte natural dels ordinals.
De la mateixa manera que 2ω és més gran que ω + n per a qualsevol nombre natural n, hi ha un nombre surreal ω2 que és infinit però més petit que ω − n per a qualsevol nombre natural n. Això és, ω2 està definit per
- ω2 = { S∗ | ω − S∗ }
on al costat dret s'utilitza la notació x − Y per significar { x − y : y ∈ Y }. Es pot identificar com el producte de ω i la forma { 0 | 1} de 12. L'aniversari de ω2 és l'ordinal límit 2ω.
Potències de ω i la forma normal de Conway
[modifica]Per classificar els «ordres» dels nombres surreals infinits i infinitesimals, també coneguts com a classes arquimedianes, Conway associa a cada nombre surreal x el nombre surreal
- ωx = { 0, r ωxL | s ωxR },
on r i s van sobre els nombres reals positius. Si x < y aleshores ωy és «infinitament més gran» que ωx, ja que és més gran que r ωx per a tots els nombres reals r. Les potències de ω també compleixen les condicions
- ωx ωy = ωx+y,
- ω−x = 1ωx,
de manera que es comporten de la manera que hom esperaria que es comportin les potències.
Cada potència de ω també té la característica redemptora de ser el nombre surreal més simple de la seva classe arquimediana; per contra, cada classe arquimediana dins dels nombres surreals conté un membre més simple únic. Així, per a cada nombre surreal positiu x sempre existirà algun nombre real positiu r i algun nombre surreal y de manera que x − rωy sigui «infinitament més petit» que x. L'exponent y és el «logaritme de base ω» de x, definit en els surreals positius; es pot demostrar que logω mapeja els surreals positius sobre els surreals i per tant
- logω(xy) = logω(x) + logω(y).
Això s'estén per inducció transfinita de manera que cada nombre surreal té una «forma normal» anàloga a la forma normal de Cantor per als nombres ordinals. Aquesta és la forma normal de Conway: cada nombre surreal x es pot escriure de manera única com
- x = r0ωy0 + r1ωy1 + ...,
on cada rα és un nombre real diferent de zero i els yα formen una seqüència estrictament decreixent de nombres surreals. Però aquesta «suma» pot tenir una infinitat de termes, i en general té la longitud d'un nombre ordinal arbitrari (el zero correspon, per descomptat, al cas d'una seqüència buida, i és l'únic nombre surreal sense exponent principal.)
Mirats d'aquesta manera, els nombres surreals s'assemblen a un cos de sèries de potències, excepte que les seqüències decreixents d'exponents han d'estar limitades en longitud per un ordinal i no es permet que siguin tan llargues com la classe dels ordinals. Aquesta és la base per a la formulació dels nombres surreals com una sèrie de Hahn.
Buits i continuïtat
[modifica]En contrast amb els nombres reals, un subconjunt (propi) dels nombres surreals no té una cota mínima superior (o inferior) tret que tingui un element màxim (mínim). Conway defineix[6] un buit com { L | R } tal que cada element de L és menor que cada element de R, i L ∪ R = ; aquest no és un nombre perquè almenys un dels costats és una classe adequada. Tot i que semblants, els buits no són els mateixos que els talls de Dedekind,[Nota 3] però encara podem parlar d'una finalització dels nombres surrealists amb l'ordenació natural que és un continu lineal (de mida de classe adequada).[10]
Per exemple, no hi ha menys surreals positius infinits, sinó un buit
- ∞ = {x: ∃ n ∈ : x < n | x: ∀ n ∈ : x > n}
que és més gran que tots els nombres reals i menor que tots els surreals infinits positius i, per tant, és el límit superior mínim dels reals en . De la mateixa manera, el buit = { | } és més gran que tots els nombres surreals (en la construcció general dels ordinals, α «és» el conjunt d'ordinals més petits que α, i podem utilitzar aquesta equivalència per escriure α = { α | } en els surreals; denota la classe dels nombres ordinals, i perquè és cofinal en tenim { | } = { | } = per extensió).
Amb una mica de cura teòrica de conjunts,[Nota 4] es pot equipar amb una topologia on els conjunts oberts són unions d'intervals oberts (indexats per conjunts adequats) i es poden definir funcions contínues.[10] També es pot definir un equivalent de successions de Cauchy, encara que s'han d'indexar per la classe d'ordinals; aquests sempre convergiran, però el límit pot ser un nombre o un buit que es pot expressar com
amb aα decreixent i sense límit inferior en (tots aquests buits es poden entendre com a successions de Cauchy, però hi ha altres tipus de buits que no són límits, com ara ∞ i ).[10]
Funció exponencial
[modifica]Basat en un treball inèdit de Kruskal, Gonshor va dur a terme una construcció (per inducció transfinita) que amplia la funció exponencial real exp(x) (amb base e) als surreals.[9]
Altres funcions exponencials
[modifica]Les potències de la funció ω també és una funció exponencial, però no té les propietats desitjades per a una extensió de la funció als reals. No obstant això, serà necessari en el desenvolupament de l'exponencial basee, i és aquesta funció la que s'entén sempre que s'utilitza la notació ωx a continuació.
Quan y és una fracció diàdica, la funció de potència x ∈ , x ↦ xy pot estar compost per multiplicació, inversa multiplicativa i arrel quadrada, tots els quals es poden definir inductivament. Els seus valors estan completament determinats per la relació bàsica xy+z = xy · xz, i quan es defineix concorda necessàriament amb qualsevol altra exponenciació que pugui existir.
Inducció bàsica
[modifica]Els passos d'inducció per a l'exponencial surreal es basen en el desenvolupament en sèrie de l'exponencial real,
més concretament aquelles sumes parcials que es poden demostrar per àlgebra bàsica com a positives però inferiors a totes les posteriors. Per a x positiu aquests es denoten [x]n i inclouen totes les sumes parcials; per a x negatiu però finit, [x]2n+1 denota els passos senars de la sèrie a partir del primer amb una part real positiva (que sempre existeix). Per a x infinit negatiu les sumes parcials senars són estrictament decreixents i la notació [x]2n+1 denota el conjunt buit, però resulta que els elements corresponents no són necessaris en la inducció.
Les relacions que es compleixen per real x < y són aleshores
- exp x · [y–x]n < exp y
i
- exp y · [x–y]2n+1 < exp x,
i això es pot estendre als surreals amb la definició
- exp z = { 0, exp zL · [z–zL]n, exp zR · [z–zR]2n+1 | exp zR / [zR–z]n, exp zL / [zL–z]2n+1 }.
Això està ben definit per a tots els arguments surreals (el valor existeix i no depèn de l'elecció de zL i zR).
Resultats
[modifica]Utilitzant aquesta definició, es compleix el següent:[Nota 5]
- exp és una funció positiva estrictament creixent, x < y ⇒ 0 < exp x < exp y
- exp satisfà exp(x+y) = exp x · exp y
- exp és una surjecció (a sobre ) i té una inversa ben definida, log = exp–1
- exp coincideix amb la funció exponencial habitual en els reals (i per tant exp 0 = 1, exp 1 = e)
- Per a x infinitesimal, el valor de la sèrie de potències formal (desenvolupament de Taylor) de exp està ben definit i coincideix amb la definició inductiva
- Quan x es dona en forma normal de Conway, el conjunt d'exponents del resultat està ben ordenat i els coeficients són sumes finites, donant directament la forma normal del resultat (que té un 1 inicial).
- De la mateixa manera, per a x infinitesimament proper a 1, el log x ve donat pel desenvolupament en sèrie de potències de x –
- Per a x infinit positiu, exp x també és infinit
- Si x té la forma ωα (α > 0), exp x té la forma ωωβ on β és una funció estrictament creixent de α. De fet, hi ha una bijecció :g: → : α ↦ β definida inductivament, la inversa de la qual també es pot definir inductivament
- Si x és «infinit pur» amb la forma normal x = Σα<βrαωaα on tots els aα > 0, aleshores exp x = ωΣα<βrαωg(aα)
- De la mateixa manera, per a x = ωΣα<βrαωbα, la inversa ve donada per log x = Σα<βrαωg–1(bα)
- Qualsevol nombre surreal es pot escriure com la suma d'un infinit pur, una part real i una part infinitesimal, i l'exponencial és el producte dels resultats parcials donats anteriorment.
- La forma normal es pot escriure multiplicant la part infinita (una única potència de ω) i l'exponencial real en la sèrie de potències resultant de la infinitesimal
- Per contra, dividint el terme principal de la forma normal portarà qualsevol nombre surreal a la forma (ωΣγ<δtγωbγ)·r·(1 + Σα<βsαωaα), per a aα < 0, on cada factor té una forma per a la qual una manera de càlcul del logaritme s'ha donat més amunt; la suma és aleshores el logaritme general
- Tot i que no hi ha una definició inductiva general de log (a diferència de exp), els resultats parcials es donen en termes d'aquestes definicions. D'aquesta manera, el logaritme es pot calcular explícitament, sense fer referència al fet que és la inversa de l'exponencial.
- La funció exponencial és molt més gran que qualsevol potència finita
- Per a qualsevol x infinit positiu i qualsevol n finit, exp(x)/xn és infinit
- Per a qualsevol nombre enter n i surreal x > n2, exp(x) > xn. Aquesta restricció més forta és un dels axiomes de Ressayre per al camp exponencial real[8]
- exp satisfà tots els axiomes de Ressayre per al camp exponencial real[8]
- Els surreals amb exponencial és una extensió elemental del camp exponencial real
- Per a εβ, un nombre èpsilon ordinal, el conjunt de nombres surreals amb aniversari menor que εβ constitueix un camp tancat sota exponencials, i també és una extensió elemental del camp exponencial real.
Exemples
[modifica]L'exponenciació surreal ve donada essencialment pel seu comportament sobre potències positives de ω, és a dir, la funció g(a), combinada amb un comportament conegut en nombres finits. Només es donaran exemples del primer. A més, g(a) = a és vàlid per a una gran part del seu rang, per exemple per a qualsevol nombre finit amb part real positiva i qualsevol nombre infinit que sigui menor que una potència iterada de ω (ωω··ω per a un cert nombre de nivells).
- exp ω = ωω
- exp ω1/ω = ω i log ω = ω1/ω
- exp (ω · log ω) = exp (ω · ω1/ω) = ωω(1 + 1/ω)
- Això demostra que la funció «potència de ω» no és compatible amb exp, ja que la compatibilitat requeriria un valor de ωω aquí
- exp ε0 = ωωε0 + 1
- log ε0 = ε0 / ω
Exponenciació
[modifica]Una exponenciació general es pot definir com xy = exp(y · log x), donant una interpretació a expressions com2ω = exp(ω · log 2) = ωlog 2 · ω. De nou, és essencial distingir aquesta definició de la funció «potències de ω», especialment si ω pot aparèixer com a base.
Nombres surcomplexos
[modifica]Un nombre surcomplex és un nombre de la forma a+bi, on a i b són nombres surreals i és l'arrel quadrada de -1.[11][12] Els nombres surcomplexos formen un cos algebraicament tancat (excepte per ser una classe pròpia), isomòrfic a la clausura algebraica del cos generat per estendre els nombres racionals per una classe pròpia d'elements transcendents algebraicament independents. Fins a l'isomorfisme de cos, aquest fet caracteritza el cos dels nombres surcomplexos dins de qualsevol teoria de conjunts fixos.[13]
Jocs
[modifica]La definició de nombres surreals contenia una restricció: cada element de L ha de ser estrictament inferior a cada element de R. Si s'elimina aquesta restricció podem generar una classe més general coneguda com a «jocs». Tots els jocs es construeixen d'acord amb aquesta regla:
- Norma de construcció
- Si L i R són dos jocs llavors { L | R } és un joc.
La suma, la negació i la comparació es defineixen de la mateixa manera tant per als nombres surreals com per als jocs.
Cada nombre surreal és un joc, però no tots els jocs són números surreals (per exemple, el joc {0 | 0} no és un nombre surreal). La classe de jocs és més general que els surreals i té una definició més senzilla, però no té algunes de les propietats més agradables dels nombres surreals. La classe dels nombres surreals forma un cos, però la classe dels jocs no. Els surreals tenen un ordre total: donats dos surreals qualsevol, o són iguals o un és més gran que l'altre. Els jocs només tenen un ordre parcial: existeixen parelles de jocs que no són ni iguals, ni més grans ni menors entre si. Cada nombre surreal és positiu, negatiu o zero. Cada joc és positiu, negatiu, zero o difús (incomparable amb zero, com ara {1|−1}).
Un moviment en un joc implica que el jugador el moviment del qual és qui escull un joc d'entre els disponibles a L (per al jugador esquerre) o R (per al jugador dret) i després passar aquest joc escollit a l'altre jugador. Un jugador que no es pot moure perquè l'elecció és del conjunt buit ha perdut. Un joc positiu representa una victòria per al jugador esquerre, un joc negatiu per al jugador dret, un joc zero perquè el segon jugador es mogui i un joc difús perquè el primer jugador es mogui.
Si x, y i z són surreals, i x=y, aleshores x z=y z. Tanmateix, si x, y i z són jocs, i x=y, aleshores no sempre és cert que x z=y z. S'ha de tenir en compte que «=» aquí significa igualtat, no identitat.
Aplicació a la teoria combinatòria de jocs
[modifica]Els nombres surreals van ser motivats originalment per estudis del joc Go,[2] i hi ha nombroses connexions entre els jocs populars i els surreals. En aquesta secció, utilitzarem un Joc (en majúscula) per a l'objecte matemàtic {L|R}, i el joc (en minúscula) per a jocs recreatius com els Escacs o Go.
Considerem jocs amb aquestes propietats:
- Dos jugadors (anomenats esquerra i dreta; L i R)
- Determinista (el joc a cada pas dependrà completament de les eleccions que facin els jugadors, en lloc d'un factor aleatori)
- Sense informació oculta (com ara cartes o fitxes que amaga un jugador)
- Els jugadors s'alternen fent torns (el joc pot permetre o no múltiples moviments en un torn)
- Cada joc ha d'acabar amb un nombre finit de moviments
- Tan bon punt no queden moviments legals per a un jugador, el joc acaba i aquest jugador perd
Per a la majoria de jocs, la posició inicial del tauler no dona un gran avantatge a cap dels jugadors. A mesura que avança el joc i un jugador comença a guanyar, es produiran posicions del tauler en què aquest jugador tingui un clar avantatge. Per analitzar jocs, és útil associar un Joc amb cada posició del tauler. El valor d'una posició determinada serà el Joc {L|R}, on L és el conjunt de valors de totes les posicions que es poden assolir en un sol moviment per esquerra. De la mateixa manera, R és el conjunt de valors de totes les posicions que es poden assolir en un sol moviment per dreta.
El joc zero (anomenat 0) és el joc on L i R estan buits, de manera que el jugador que es mou a continuació (L o R) perd immediatament. La suma de dos jocs G = { L1 | R1 } i H = { L2 | R2 } es defineix com el Joc G + H = { L1 + H, G + L2 | R1 + H, G + R2 } on el jugador a moure tria a quin dels Jocs jugar en cada etapa, i el perdedor segueix sent el jugador que acaba sense moviment legal. Es pot imaginar dos taulers d'escacs entre dos jugadors, amb jugadors fent moviments alternativament, però amb total llibertat quant a quin tauler jugar. Si G és el joc {L | R}, -G és el joc {-R | -L}, és a dir, amb el paper dels dos jugadors invertit. És fàcil mostrar G - G = 0 per a tots els Jocs G (on G - H es defineix com G + (-H)).
Aquesta manera senzilla d'associar Jocs amb jocs dona un resultat molt interessant. Suposem que dos jugadors perfectes juguen un joc començant per una posició donada el Joc associat de la qual és x. Podem classificar tots els Jocs en quatre classes de la següent manera:
- Si x > 0, Esquerra (L) guanyarà, independentment de qui jugui primer.
- Si x < 0, Dreta (R) guanyarà, independentment de qui jugui primer.
- Si x = 0, guanyarà el jugador que vagi segon.
- Si x || 0 llavors el jugador que vagi primer guanyarà.
De manera més general, podem definir G > H com G - H > 0, i de manera similar per a <, = i ||.
La notació G || H significa que G i H són incomparables. G || H és equivalent a G−H || 0, és a dir, que G > H, G < H i G = H són tots falsos. De vegades es diu que els jocs incomparables es confonen entre si, perquè un jugador pot preferir un o l'altre segons el que s'hi afegeixi. Es diu que un joc confós amb zero és difús, en oposició a positiu, negatiu o zero. Un exemple de joc difús és l'estrella (*).
De vegades, quan una partida s'acosta al final, es descompondrà en diverses partides més petites que no interactuen, excepte que el torn de cada jugador permet moure's només en una d'elles. Per exemple, al Go, el tauler s'omplirà lentament de peces fins que només hi hagi unes quantes petites illes d'espai buit on un jugador es pugui moure. Cada illa és com un joc separat de Go, jugat en un tauler molt petit. Seria útil que cada subjoc es pogués analitzar per separat, i després els resultats es combinessin per donar una anàlisi de tot el joc. Això no sembla ser fàcil de fer. Per exemple, hi pot haver dos subjocs en què guanya qui es mou primer, però quan es combinen en un gran joc, ja no és el primer jugador qui guanya. Afortunadament, hi ha una manera de fer aquesta anàlisi. Es pot aplicar el teorema següent:
- Si un joc gran es descompon en dos jocs més petits, i els jocs petits tenen Jocs associats de x i y, aleshores el joc gran tindrà un Joc associat de x+y.
Un joc compost de jocs més petits s'anomena suma disjuntiva d'aquests jocs més petits, i el teorema estableix que el mètode d'addició que hem definit és equivalent a prendre la suma disjuntiva dels sumands.
Històricament, Conway va desenvolupar la teoria dels nombres surreals en l'ordre invers a com s'ha presentat aquí. Estava analitzant els jocs finals del Go i es va adonar que seria útil tenir alguna manera de combinar les anàlisis dels subjocs que no interactuen en una anàlisi de la seva suma disjuntiva. A partir d'això va inventar el concepte de Joc i l'operador d'addició per aquest. A partir d'aquí va passar a desenvolupar una definició de negació i comparació. Aleshores es va adonar que una determinada classe de Jocs tenia propietats interessants; aquesta classe es va convertir en els números surreals. Finalment, va desenvolupar l'operador de multiplicació i va demostrar que els surreals són en realitat un cos, i que inclou tant els reals com els ordinals.
Realitzacions alternatives
[modifica]Aproximacions alternatives als números surreals complementen l'exposició de Conway en termes de jocs.
Desenvolupament del signe
[modifica]Definicions
[modifica]En el que ara s'anomena desenvolupament de signes o seqüència de signes d'un nombre surreal, un nombre surreal és una funció el domini del qual és un ordinal i el codomini de la qual és { −1, +1 }.[14] Això és equivalent a les seqüències L-R de Conway.[6]
Definim el predicat binari «més simple que» en nombres per x és més simple que y si x és un subconjunt propi de y, és a dir, si dom(x) < dom(y) i x(α) = y(α) per a tot α < dom (x).
Per als nombres surreals, definim la relació binària < com a ordre lexicogràfic (amb la convenció que els «valors indefinits» són majors que -1 i menors que 1). Per tant, x < y si es compleix una de les opcions següents:
- x és més senzill que y i y(dom(x)) = + 1;
- y és més senzill que x i x(dom(y)) = − 1;
- existeix un nombre z tal que z és més simple que x, z és més simple que y, x(dom(z)) = − 1 i y(dom(z)) = + 1.
De forma equivalent, fem δ(x,y) = min({ dom(x), dom(y)} ∪ { α : α < dom(x) ∧ α < dom(y) ∧ x(α) ≠ y(α) }), i que x = y si i només si δ(x,y) = dom(x) = dom(y). Aleshores, per als nombres x i y, x < y si i només si es compleix un dels següents:
- δ(x,y) = dom(x) ∧ δ(x,y) < dom(y) ∧ y(δ(x,y)) = + 1;
- δ(x,y) < dom(x) ∧ δ(x,y) = dom(y) ∧ x(δ(x,y)) = − 1;
- δ(x,y) < dom(x) ∧ δ(x,y) < dom(y) ∧ x(δ(x,y)) = − 1 ∧ y(δ(x,y)) = + 1.
Per als nombres x i y, x ≤ y si i només si x < y ∨ x = y, i x > y si i només si y < x. Llavors x ≥ y si i només si y ≤ x.
La relació < és transitiva, i per a tots els nombres x i y, es compleix exactament un de x < y, x = y, x > y (llei de la tricotomia). Això vol dir que < és un ordre lineal (excepte que < és una classe pròpia).
Per als conjunts de nombres, L i R de tal manera que ∀x ∈ L ∀y ∈ R (x < y), existeix un nombre únic z tal que
- ∀x ∈ L (x < z) ∧ ∀y ∈ R (z < y),
- Per a qualsevol nombre w tal que ∀x ∈ L (x < w) ∧ ∀y ∈ R (w < y), w = z o z és més senzill que w.
A més, z és construïble a partir de L i R per inducció transfinita. z és el nombre més simple entre L i R.
Sigui el nombre únic z denotat per σ(L,R). Per a un nombre x, es defineix el seu conjunt esquerre L(x) i el seu conjunt dret R(x) per
- L(x) = { x|α : α < dom(x) ∧ x(α) = + 1 };
- R(x) = { x|α : α < dom(x) ∧ x(α) = − 1 },
llavors σ(L(x),R(x)) = x.
Un avantatge d'aquesta realització alternativa és que la igualtat és identitat, no una relació definida inductivament. Però a diferència de la realització de Conway dels nombres surreals, el desenvolupament de signes requereix una construcció prèvia dels ordinals, mentre que en la realització de Conway, els ordinals es construeixen com a casos particulars de surreals.
Tanmateix, es poden fer definicions similars que eliminen la necessitat de construir prèviament els ordinals. Per exemple, es pot deixar que els surreals siguin la classe (definida recursivament) de funcions el domini de les quals és un subconjunt dels surreals que compleixen la regla de transitivitat ∀g ∈ dom f (∀h ∈ dom g (h ∈ dom f)) i les quals l'interval és { −, + }. «Més senzill que» es defineix de manera molt senzilla ara: x és més simple que y si x ∈ dom y. L'ordenació total es defineix considerant x i y com a conjunts de parells ordenats (com es defineix normalment una funció): o bé x = y, o bé el nombre surreal z = x ∩ y es troba en el domini de x o en el domini de y (o tots dos, però en aquest cas els signes han de no estar d'acord). Aleshores tenim x < y si x(z) = − o y(z) = + (o tots dos). Convertir aquestes funcions en seqüències de signes és una tasca senzilla; ordena els elements de dom f per ordre de simplicitat (és a dir, inclusió) i després escriu els signes que f assigna a cadascun d'aquests elements per ordre. Aleshores, els ordinals apareixen de manera natural com aquells nombres surreals el rang dels quals és { + }.
Addicció i multiplicació
[modifica]La suma x + y de dos nombres, x i y, es defineix per inducció a dom(x) i dom(y) per x + y = σ(L,R), on
- L = { u + y : u ∈ L(x) } ∪{ x + v : v ∈ L(y) },
- R = { u + y : u ∈ R(x) } ∪{ x + v : v ∈ R(y) }.
La identitat additiva ve donada pel nombre 0 = { }, és a dir, el nombre 0 és la funció única el domini de la qual és l'ordinal 0, i l'invers additiu del nombre x és el nombre − x, donat per dom(− x) = dom(x) i, per a α < dom(x), (− x)(α) = − 1 si x(α) = + 1, i (− x)(α) = + 1 si x(α) = − 1.
Es dedueix que un nombre x és positiu si i només si 0 < dom(x) i x(0) = + 1, i x és negatiu si i només si 0 < dom(x) i x(0) = − 1.
El producte xy de dos nombres, x i y, es defineix per inducció sobre dom(x) i dom(y) per xy = σ(L,R), on
- L = { uy + xv − uv : u ∈ L(x), v ∈ L(y) } ∪ { uy + xv − uv : u ∈ R(x), v ∈ R(y) },
- R = { uy + xv − uv : u ∈ L(x), v ∈ R(y) } ∪ { uy + xv − uv : u ∈ R(x), v ∈ L(y) }.
La identitat multiplicativa ve donada pel nombre 1 = { (0,+ 1) }, és a dir, el nombre 1 té un domini igual a l'ordinal 1, i 1(0) = + 1.
Correspondència amb la realització de Conway
[modifica]El mapa des de la realització de Conway fins als desenvolupaments de signes ve donat per f({ L | R }) = σ(M,S), on M = { f(x) : x ∈ L } i S = { f(x) : x ∈ R }.
El mapa invers de la realització alternativa a la realització de Conway ve donat per g(x) = { L | R }, on L = { g(y) : y ∈ L(x) } i R = { g(y) : y ∈ R(x) }.
Aproximació axiomàtica
[modifica]En un altre enfocament dels surreals, donat per Alling,[12] la construcció explícita es passa per alt. En canvi, es dona un conjunt d'axiomes que qualsevol enfocament particular dels surreals ha de satisfer. Igual que l'aproximació axiomàtica dels reals, aquests axiomes garanteixen la singularitat fins a l'isomorfisme.
Un triplet és un sistema de nombres surreals si i només si es compleix el següent:
- < és un ordre total sobre
- b és una funció de a la classe de tots els ordinals (b s'anomena «funció d'aniversari» de ).
- Siguin A i B subconjunts de tal que per a tot x ∈ A i y ∈ B, x < y (utilitzant la terminologia d'Alling, 〈 A,B 〉 és un «tall de Conway» de ). Aleshores existeix un únic z ∈ tal que b(z) és mínim i per a tot x ∈ A i tot y ∈ B, x < z < y (aquest axioma s'anomena sovint «Teorema de la simplicitat de Conway»).
- A més, si un ordinal α és més gran que b(x) per a tot x ∈ A, B, aleshores b(z) ≤ α (Alling anomena un sistema que compleix aquest axioma un «sistema de nombres surreals complet»).
Tant la construcció original de Conway com la construcció de desenvolupament de signes dels surreals satisfan aquests axiomes.
Tenint en compte aquests axiomes, Alling[12] deriva la definició original de Conway de ≤ i desenvolupa l'aritmètica surreal.
Simplicitat jeràrquica
[modifica]Una construcció dels nombres surreals com a pseudo-arbre binari màxim amb simplicitat (ancestre) i relacions d'ordenació es deu a Philip Ehrlich.[15] La diferència amb la definició habitual d'un arbre és que el conjunt dels avantpassats d'un vèrtex està ben ordenat, però pot no tenir un element màxim (predecessor immediat); en altres paraules, el tipus d'ordre d'aquest conjunt és un nombre ordinal general, no només un nombre natural. Aquesta construcció també compleix els axiomes d'Alling i es pot mapejar fàcilment a la representació de la seqüència de signes.
Sèries de Hahn
[modifica]Alling[16] també demostra que el cos dels nombres surreals és isomòrfic (com a cos ordenat) al cos de les sèries de Hahn amb coeficients reals sobre el grup de valors dels mateixos nombres surreals (la representació de la sèrie corresponent a la forma normal d'un nombre surreal, tal com es defineix mès a dalt). Això proporciona una connexió entre els nombres surreals i els enfocaments matemàtics més convencionals de la teoria de cossos ordenats.
Aquest isomorfisme converteix els nombres surreals en un cos valorat on la valoració és la inversa additiva de l'exponent del terme principal en la forma normal de Conway, per exemple, ν(ω) = -1. L'anell de valoració consisteix llavors en els nombres surreals finits (nombres amb una part real i/o infinitesimal). El motiu de la inversió de signe és que els exponents en la forma normal de Conway constitueixen un conjunt inversament ben ordenat, mentre que les sèries de Hahn es formulen en termes de subconjunts (no invertits) ben ordenats del grup de valors.
Relació amb els nombres hiperreals
[modifica]Philip Ehrlich ha construït un isomorfisme entre el camp numèric surreal màxim de Conway i els hiperreals màxims en la teoria de conjunts de von Neumann-Bernays-Gödel.[15]
Notes
[modifica]- ↑ En la formulació original utilitzant la Teoria de conjunts de von Neumann-Bernays-Gödel, els surreals formen una classe pròpia, en lloc d'un conjunt, de manera que el terme cos no és precisament correcte; on aquesta distinció és important, alguns autors utilitzen «cos» per referir-se a una classe adequada que té les propietats aritmètiques d'un camp. Es pot obtenir un cos veritable limitant la construcció a un univers de Grothendieck, donant un conjunt amb la cardinalitat d'algun cardinal fortament inaccessible, o utilitzant una forma de teoria de conjunts en la qual es construeixen per recursivitat transfinita aturant-se en algun ordinal comptable com ara ε0.
- ↑ El conjunt de fraccions diàdiques constitueix el grup i anell no trivial més simple d'aquest tipus; consisteix en els nombres surrealistes amb aniversari inferior a ω = ω1 = ωω0.
- ↑ La definició d'un buit omet les condicions d'un tall de Dedekind que L i R no siguin buits i que L no tinguin un element més gran, i també la identificació d'un tall amb l'element més petit de R si existeix.
- ↑ És important destacar que no hi ha cap afirmació que la col·lecció de successions de Cauchy constitueixi una classe en la teoria de conjunts NBG.
- ↑ Fins i tot l'aspecte més trivial d'aquestes igualtats pot implicar una inducció transfinita i constituir un teorema separat.
Referències
[modifica]- ↑ 1,0 1,1 Bajnok, 2013.
- ↑ 2,0 2,1 O'Connor, J. J.; Robertson, E. F. «Conway Biography» (en anglès). MacTutor.
- ↑ Knuth, Donald. «Surreal Numbers» (en anglès). Stanford Unviersity.
- ↑ 4,0 4,1 Alling, 1962, p. 341-352.
- ↑ Alling, 1985, p. 365-386.
- ↑ 6,0 6,1 6,2 Conway, 2000.
- ↑ Conway, 2000, p. 21.
- ↑ 8,0 8,1 8,2 8,3 van den Dries i Ehrlich, 2001, p. 173-188.
- ↑ 9,0 9,1 Gonshor, 1986, p. cap. 10.
- ↑ 10,0 10,1 10,2 Rubinstein Salzedo, Swaminathan.
- ↑ Propp, James. «Surreal vectors and the game of Cutblock» (en anglès), 22-08-1994.
- ↑ 12,0 12,1 12,2 Alling, 1987.
- ↑ Conway, 2000, p. Teorema 21.
- ↑ Gonshor, 1986, p. cap. 2.
- ↑ 15,0 15,1 Ehrlich, 2012, p. 145.
- ↑ Alling, 1987, p. 246; teorema 6.55.
Bibliografia
[modifica]- Alling, Norman L. «On the existence of real-closed fields that are ηα-sets of power ℵα» (en anglès). Trans. Amer. Math. Soc., 103, 1962. DOI: 10.1090/S0002-9947-1962-0146089-X.
- Alling, Norman L. «Conway's Field of surreal numbers» (
 PDF) (en anglès). Trans. Amer. Math. Soc., 287(1), gener 1985. DOI: 10.1090/s0002-9947-1985-0766225-7.
PDF) (en anglès). Trans. Amer. Math. Soc., 287(1), gener 1985. DOI: 10.1090/s0002-9947-1985-0766225-7. - Alling, Norman L. Foundations of Analysis over Surreal Number Fields (en anglès). North-Holland, 1987 (Mathematics Studies 141). ISBN 0-444-70226-1.
- Badiou, Alain. Number and Numbers (en anglès). Nova York: Polity Press, 2008. Un desenvolupament filosòfic detallat del concepte de nombre surreal com a concepte més general.
- Bajnok, Béla. An Invitation to Abstract Mathematics (en anglès), 2013. ISBN 9781461466369. Teorema 24.29. The surreal number system is the largest ordered field.
- Conway, John H. On Numbers and Games (en anglès). CRC Press, 2000. ISBN 9781568811277. Any original: 1976.
- Conway, John H. On Numbers and Games (en anglès), 2001. Una actualització del llibre de 1976 que defineix els nombres surreals, i explora la seva connexión amb jocs.
- Ehrlich, Philip «The absolute arithmetic continuum and the unification of all numbers great and small» (
 PDF) (en anglès). The Bulletin of Symbolic Logic, 18(1), 2012. Arxivat de l'original el 2017-10-07. DOI: 10.2178/bsl/1327328438 [Consulta: 18 febrer 2023].
PDF) (en anglès). The Bulletin of Symbolic Logic, 18(1), 2012. Arxivat de l'original el 2017-10-07. DOI: 10.2178/bsl/1327328438 [Consulta: 18 febrer 2023]. - Gardner, Martin. «Cap. 4. A non-technical overview». A: Penrose Tiles to Trapdoor Ciphers (en anglès). W. H. Freeman & Co., 1989. Reeimpressió de l'article del Scientific American de 1976.
- Gonshor, Harry. An Introduction to the Theory of Surreal Numbers. 110. Cambridge University Press, 1986 (London Mathematical Society Lecture Note Series). DOI 10.1017/CBO9780511629143. ISBN 9780521312059. Un tractament dels nombres surreals basat en la realització del desenvolupament del signe.
- Knuth, Donald. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness (en anglès), 1974. Exposició original.
- Rubinstein Salzedo, Simon; Swaminathan, Ashvin. Analysis on Surreal Numbers (en anglès), maig 2015.
- Shulman, Polly «Infinity Plus One, and Other Surreal Numbers» (en anglès). Discover, desembre 1995.
- van den Dries, Lou; Ehrlich, Philip «Fields of surreal numbers and exponentiation» (en anglès). Institute of Mathematics of the Polish Academy of Sciences [Varsòvia], 167(2), gener 2001. DOI: 10.4064/fm167-2-3. ISSN: 0016-2736.
- The Univalent Foundations Program. Homotopy Type Theory: Univalent Foundations of Mathematics. Princeton, NJ: Institute for Advanced Study], 2013. S'estudien els nombres surreals en el context de la homotopy type theory en la secció 11.6.