Valor propi, vector propi i espai propi

Figura 1. Aquesta aplicació lineal deforma l'estàtua de David. Els vectors blaus tenen per a imatges els vectors verds. Conserven la mateixa direcció, per tant són vectors propis. El valor propi associat és -1/2 (perquè canvien de sentit i el mòdul és la meitat). En aquest cas particular l'espai propi és l'espai sencer.

Figura. 2. En aquesta aplicació lineal el quadre de la Mona Lisa, es transforma de tal manera que els vectors de l'eix vertical central (vector vermell) no ha canviat ni de direcció ni de sentit ni de mòdul, en canvi el vector diagonal (blau) ha canviat de direcció. En aquest cas el vector vermell és un vector propi de l'aplicació però el vector blau no ho és. Com que el vector vermell no ha canviat ni de direcció ni de mòdul, el seu valor propi és 1. Tots els vectors amb la mateixa direcció que el vector vermell són també vectors propis, amb el mateix valor propi. Tots junts, afegint-hi el vector zero formen l'espai propi d'aquesta aplicació que en aquest cas és un espai de dimensió 1.

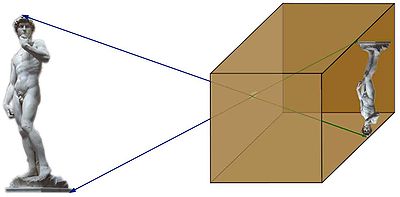
En matemàtiques, i més concretament en àlgebra el concepte de vector propi és una noció que es refereix a una aplicació lineal d'un espai en si mateix. Correspon a l'estudi dels eixos privilegiats, en els quals l'aplicació es comporta com una dilatació (o contracció si el mòdul del valor propi és més petit que 1), per tant, els vectors imatge en aquesta direcció corresponen als vectors origen multiplicats per una constant (si és negativa vol dir que canvien de sentit, però en cap cas no canvien de direcció). D'aquest factor que multiplica el vector origen per trobar el vector imatge se'n diu valor propi, el conjunt format per tots els vectors propis amb un mateix valor propi més el vector nul és un espai propi. Els gràfics de les figures 1 i 2 il·lustren aquestes nocions.

El coneixement dels vectors i valors propis ofereix una informació clau sobre l'aplicació lineal en qüestió. Existeixen a més nombrosos casos en què aquest coneixement caracteritza totalment l'aplicació lineal.

Aquest concepte originalment pertanyia a la branca de les matemàtiques anomenada àlgebra lineal. La seva utilització, tanmateix, avui en dia supera de lluny aquest marc. Intervé tant en matemàtiques pures com en matemàtiques aplicades. Apareix per exemple en geometria en l'estudi de les formes quadràtiques, o en anàlisi funcional. Permet resoldre problemes aplicats tan variats com el del moviment d'una corda vibrant, la classificació de les pàgines web per Google, la determinació de l'estructura de l'espaitemps en la teoria de la relativitat general, o l'estudi de l'equació de Schrödinger en mecànica quàntica.

A banda de la terminologia habitual de valors i vectors propis n'hi ha d'altres força esteses. Per exemple, hi ha qui parla d'autovalor, autovector i autoespai. Seguint la nomenclatura original de l'alemany, també es fa servir la denominació de eigenvalor, eigenvector i eigenespai, on la paraula eigen precisament significa "propi". Una altra variant usada en mecànica i enginyeria és la de valor i vector característic (per la relació amb el polinomi característic). Finalment, sí que és molt freqüent l'ús de les abreviatures vap i vep, fins al punt d'utilitzar-se com a paraules a l'hora de formar plural (vaps i veps).

Història

Gènesi

René Descartes connecta l'àlgebra i la geometria, comença l'àlgebra lineal.

Si bé és habitual prendre com a partida de naixement oficial de l'àlgebra la publicació del llibre d'Al-Khwarazmí (783-850), que es descriu a si mateix com «un compendi que engloba les més fines i les més nobles operacions del càlcul», l'àmbit de l'àlgebra lineal ha d'esperar al segle xvi per anar més enllà de marc elemental d'algunes equacions.

L'associació entre la geometria i l'àlgebra, a través de la noció de coordenades, va ser introduïda el 1637 per René Descartes (1596-1650) i Pierre de Fermat (1601-1665). Amb això queda establert el context per a l'aparició dels primers resultats d'àlgebra lineal com ara el càlcul d'un determinant. Aquests resultats serviran més tard d'eina d'anàlisi dels valors propis. Tanmateix, les matemàtiques d'aquesta època no disposen encara de les nocions indispensables de l'àlgebra lineal, com una geometria que correspongui al nostre espai vectorial, on els elements es defineixen per les seves operacions.

El començament del segle xix veu l'aparició d'eines importants per a la teoria dels valors propis. El 1799, Carl Friedrich Gauss (1777-1855) demostrà el Teorema fonamental de l'àlgebra. S'estudien espais vectorials més amplis. Gauss formalitzà el problema de la resolució d'un sistema d'equacions lineals amb el mètode del pivot retrobant un mètode que ja havia estat descrit abans per un matemàtic xinès Liu Hui (Segle III) gairebé 1600 anys abans.

S'estudien problemes on els valors propis resultaran ser l'enfocament més adequat. Joseph Fourier (1768-1830) estudià una solució de l'equació de conducció calorífica amb l'ajuda d'una eina que més tard es dirà una base de vectors propis. Finalment el 1834, Hamilton (1805-1865) fa servir un polinomi característic per a trobar el que ara es diu els valors propis associats a l'endomorfisme d'una equació diferencial lineal de primer ordre que apareix en plantejar un problema de mecànica. Tanmateix, l'absència de formalització suficient de la noció d'espai vectorial impedeix l'aparició clara del concepte.

Origen de la paraula

L'alemany Hilbert dona la nomenclatura anglosaxona: eigenvalue que prové de Eigenwert.

La formalització algebraica dels espais vectorials apareix cap a mitjans del segle. Arthur Cayley (1821-1895) inicia l'estudi dels espais vectorials de dimensió n i de les seves aplicacions lineals. Grassmann (1809-1877) formalitzà el concepte. Però en tant que matemàtic és poc reconegut per aquesta època, des de 1845, Cauchy (1789-1857) reprengué idees anàlogues i les publicà sota una forma més definitiva nou anys més tard. Sylvester (1814-1897), en col·laboració amb Cayley, utilitzà per primera vegada el terme matriu el 1850. Dos anys més tard, utilitzà la noció de valor propi en el cas de les formes bilineals per a la resolució de problemes basats en el principi mecànic de la inèrcia. Finalment Cayley el 1858 definí la noció de matriu de manera general i abstracta.

El francès Jordan donà la nomenclatura francesa de la qual deriva la catalana: valor propi.

Jordan (1838-1922) publicà un llibre definitiu sobre els endomorfismes de dimensió finita i per a una àmplia família de nombres, entre els quals els complexos i els reals. Jordan analitzà el paper dels vectors propis i del seu àmbit d'aplicació exacte en una teoria que ara es coneix amb el nom de reducció d'endomorfismes. La finalitat del seu text no és l'àlgebra lineal sinó la teoria de grups i les seves representacions. La teoria es presentà així en el context dels cossos finits. El capítol dels valors propis acaba amb el cas de la dimensió finita i dels cossos de nombres algebraicament tancats. La terminologia francesa i a partir d'aquesta la catalana prové dels treballs de Jordan.

Desenvolupament al segle xx

El començament del segle xx porta un nou punt de vista sobre la geometria. La resolució de l'equació integral porta a alguns matemàtics a considerar una geometria sobre el conjunt de les funcions. Frigyes Riesz (1880-1956) utilitza sistemes ortogonals de funcions. Erhard Schmidt (1876-1959) sosté la seva tesi sobre un subjecte anàleg sota la direcció de David Hilbert (1862-1943). Els treballs de Hilbert (1862-1943) aporten a la noció de valor propi una nova profunditat. Corresponen a la formalització del pas intuïtiu que havia portat Fourier a la resolució de l'equació de la transferència de calor. Els conjunts de funcions es veuen com un espai vectorial de dimensió infinita, la geometria del qual és calcada de la d'Euclides. L'equació integral es fa l'equivalent a un sistema lineal i l'aplicació lineal pren el nom d'operador diferencial. Neix una nova branca de les matemàtiques: l'anàlisi funcional. Aquesta nova branca esdevé ràpidament el marc general de resolució d'una àmplia família de problemes matemàtics, en particular l'anàlisi, les equacions diferencials o les equacions a les derivades parcials. Els valors propis són una de les eines essencials per a la resolució d'aquests problemes. Resulten indispensables en física per a teories com la mecànica quàntica o la relativitat general. Durant un llarg període els anglosaxons utilitzen indiferentment els termes de proper value i eigenvalue, que provenen respectivament de la traducció dels texts de Jordan i de Hilbert. El vocabulari actual s'ha fixat en benefici de la segona expressió.

Alhora en el context de la dimensió finita i per al cas general, el segle xx veu un desenvolupament massiu d'aquestes teories. El cas de dimensió finita experimenta dues evolucions: la teoria es generalitza a altres conjunts de nombres a més dels reals i els complexos. A més, matemàtics com Issai Schur, A. Krilov, W. E. Arnoldi o N. Dunford desenvolupen quantitat d'algorismes per permetre la determinació dels valors propis. Tanmateix el cas general s'estudia més profundament. S'obre la via a una branca matemàtica important al llarg d'aquest segle, l'anàlisi funcional. La teoria dels valors propis, llavors es generalitza a la teoria espectral. Paul Dirac i John von Neumann estudien aquest concepte en un marc que serveix de modelització a la física. Israel Gelfand, Mark Naimark i Irving Segal apliquen aquests conceptes a universos més vastos, les C*-àlgebres. Sobre la base de resultats de geometria algebraica trobats per Alexander Grothendieck, Alain Connes desenvolupa un cas particular de C*-àlgebres, les geometries no commutatives. La teoria espectral continua sent encara un camp ampli de recerca, i molts problemes resten sempre oberts en aquest àmbit.

Els valors propis, i en el seu cas més general, la teoria espectral obren nombrosos camps d'aplicació alhora teòrics i aplicats. En matemàtica, aquest enfocament permet, per exemple, la resolució d'equacions diferencials, o d'equacions diferencials en derivades parcials. La física utilitza molt àmpliament la teoria espectral: serveix de marc general a la mecànica quàntica i permet, per exemple, l'estudi de l'equació de Schrödinger. Les solucions de l'equació de Schrödinger independents del temps són vectors propis. Les teories físiques de finals del segle xx com les supercordes utilitzen àmpliament les nocions d'espectre en marcs matemàtics avançats, per exemple les geometries no commutatives. L'enginyeria no en queda al marge, fins i tot s'aplica general a un enfocament de dimensió finita. Utilitzen molts algorismes procedents dels càlculs de valors propis i vectors propis. Aquest enfocament permet resoldre múltiples problemes trets per exemple de l'estàtica o de la dinàmica i fins i tot problemes d'altres sectors com ara l'economia.

Definició

Definició intuïtiva

Una aplicació lineal és una funció que transforma els vectors (a cada vector de l'espai origen li assigna un vector de l'espai imatge) conservant les propietats d'addició dels vectors (el vector imatge de la suma de dos vectors és el mateix que el vector suma de les imatges de cada un) i també conserva les proporcions entre vectors col·lineals (si els mòduls de dos vectors col·lineals tenen una relació donada, per exemple un és el triple que l'altre, els vectors imatge també són col·lineals i tenen la mateixa relació, en l'exemple, el mòdul de la imatge de l'un és el triple que el mòdul de la imatge de l'altre). Així, si un vector w és la suma de dos vectors u i v, llavors la imatge de w per l'aplicació és la suma de la imatge de u i la imatge de v. A més la imatge de k v és k vegades la imatge de v. Diverses transformacions geomètriques usuals (homotècia de centre 0, rotació de centre 0) són aplicacions lineals.

La figura 3 il·lustra un exemple d'aplicació lineal. Fixeu-vos que el vector vermell és la suma dels dos vectors grocs abans de transformació, i que ho continua sent després. Igualment, el vector negre és el triple del vector verd abans de la transformació, i aquest continua sent el cas una vegada que s'ha aplicat. En el cas del vector gris, multiplicant-lo per -1 s'obté la seva imatge, per tant el vector gris és un vector propi de l'aplicació amb valor propi -1.

Figura 3. Exemple d'aplicació lineal: una simetria respecte de l'eix horitzontal

• Un vector es diu vector propi d'una aplicació lineal si és no nul i si l'aplicació no fa més que modificar el seu mòdul sense canviar la seva direcció (no confondre amb el seu sentit!) s'entén que canviar de sentit és equivalent a canviar de signe el mòdul).
• Un valor propi associat a un vector propi és el factor que multiplica el mòdul, és a dir el nombre pel qual cal multiplicar el vector per obtenir la seva imatge. Aquest factor pot ser negatiu (inversió del sentit del vector) o nul (vector es transforma en el vector nul que té longitud zero).
• Un espai propi associat a un valor propi és el conjunt dels vectors propis que tenen un mateix valor propi afegint-hi el vector nul.

Definició matemàtica

Sia E un espai vectorial sobre $\mathbb {K}$ i u un endomorfisme de E, llavors :

• El vector x de E no nul es diu que és un vector propi de u si i només si existeix un element λ de $\mathbb {K}$ tal que u(x) = λx,
• L'escalar λ, element de $\mathbb {K}$ es diu que és un valor propi de u si i només si existeix un vector x no nul de E tal que u(x) = λx,
• Sia λ un valor propi de u llavors el conjunt format pels vectors propis amb valor propi λ, conjuntament amb el vector nul, forma un subespai vectorial de E anomenat espai propi de u associat al valor propi λ.

El vocabulari dels elements propis en diferents disciplines

• En mecànica, s'estudien les freqüències pròpies i els modes propis dels sistemes oscil·lants. Les freqüències pròpies són aquelles a les que oscil·la el sistema en absència de forces d'acció i de forces dissipatives. Són els valors propis del sistema lineal d'equacions diferencials que descriu el comportament del sistema. Els modes propis són els vectors propis del sistema d'equacions i determinen la forma que adopta l'objecte vibrant.

Els modes propis d'una biga en voladís
1r mode de flexió lateral	1r mode de torsió	1r mode de flexió vertical
2n mode de flexió lateral	2n mode de torsió	2n mode de flexió vertical

• En Anàlisi funcional, una funció pròpia és un vector propi d'un operador lineal, és a dir d'una aplicació lineal tal que els seus conjunts origen i imatge són espais de funcions.
• En geometria analítica i en òptica, es parla de direccions pròpies per adonar de la curvatura de les superfícies.
• En teoria de grafs, un valor propi és simplement un valor propi de la matriu adjacent del graf.

Exemples

La imatge en un mirall és un bon exemple d'aplicació lineal. Tot vector enganxat al mirall dona com a imatge ell mateix. Se'n dedueix que el pla del mirall és un espai propi associat al valor propi 1. Per contra, un vector perpendicular al mirall dona com a imatge un vector d'igual longitud, igualment direcció, però de sentit oposat. Se'n dedueix que aquest vector és un vector propi de valor propi -1. Finalment un vector ni enganxat ni perpendicular dona una imatge que no està en el seu mateix eix, no és doncs un vector propi. En aquest exemple, el comportament dels vectors propis descriu integralment l'aplicació, en efecte tot vector és la suma d'un vector en el pla del mirall i d'un vector perpendicular. Per tant el coneixement del comportament en el pla del mirall i en l'eix perpendicular permet la determinació de la transformació de tots els vectors, per linearitat.

Existeix una transformació particular, que és central en la teoria dels valors propis. Imaginem com a aplicació lineal una dilatació que allunya per exemple tots els punts d'una pilota massissa de goma del seu centre en una proporció constant (per exemple en una dilatació tèrmica en augmentar la temperatura de la pilota). Aquesta dilatació engrandeix tots els vectors en una mateixa proporció sense canviar la seva direcció ni el seu sentit. Tots els vectors tret del vector nul (perquè el vector nul es pot multilicar per qualsevol escalar diferent del que es multipliquen els altres vectors i també dona el resultat correcte) són doncs els vectors propis i existeix un únic valor propi. Aquesta aplicació es diu una homotècia.

La Terra gira al voltant d'ella mateixa, i per tant tot vector que se situa a la recta que passa pels pols resta immòbil, si no es considera el moviment al voltant del Sol. Els vectors d'aquesta recta són doncs vectors propis de valor propi 1. Qualsevol altre vector girarà amb la Terra i per tant no és propi. Si l'estudi es limita al pla de l'equador, llavors tots els vectors giren i ja no hi ha vectors propis. Aquest cas particular es troba en l'estudi dels valors propis sobre els nombres reals.

Figura 4. Una ona estacionària sobre una corda vibrant és un vector propi de l'equació que regeix el moviment de la corda. En aquest exemple, aquest vector és el quart vector propi, n'hi ha infinits contables, el primer té dos punts fixos, el segon en té tres i així. Els punts fixos són els de vermell.

Els dos primers exemples tracten d'un cas de dimensió 3, com el món geomètric que ens envolta. Es poden tanmateix considerar espais vectorials de dimensió molt més gran. Un exemple d'aplicació és el de la corda vibrant per exemple la d'una guitarra. Cada punt de la corda oscil·la entorn de la seva posició de repòs. Per a cada punt de la corda, el seu moviment pot ser considerat com una dimensió d'un espai vectorial; l'espai vectorial així obtingut reagrupa els moviments de tots els punts de la corda, és de dimensió infinita. A partir d'una posició inicial obtinguda pel dit del guitarrista, el moviment de la corda segueix una equació que es diu equació diferencial en derivades parcials que és lineal. Els vectors propis són en aquest cas vibracions que deixen alguns punts fixos, se'ls en diu ones estacionàries. La figura 4 il·lustra un exemple de vibració. El primer vector propi correspon a l'ona amb dos punts fixos, els extrems, el segon vector propi correspon a l'ona que té com a punt fix suplementari el del mig, el tercer té dos punts fixos situats a un terç i a dos terços a més a més dels extrems, etcètera. Resulta que en aquest cas precís, els vectors propis descriuen totalment el comportament de la corda (qualsevol vibració és el sumatori d'una sèrie obtinguda multiplicant cada vector propi per un escalar). A més, si es té en compte en l'equació el fenomen d'esmorteïment (com que la velocitat creix en augmentar el nombre de punts fixos i el frec amb l'aire és proporcional al cub de la velocitat) resulta que les components de la vibració corresponents a la majoria dels vectors propis es dissipen molt de pressa, sol el primer vector propi resta molt de temps. Correspon a la nota que serà emesa per la corda de la guitarra que depèn doncs de la longitud de la corda però poc de la impulsió inicial.

Aplicacions en dimensió finita

Sistema d'equacions lineals i valor propi

Molts problemes s'acaben presentant sota la forma de la resolució d'un sistema d'equacions lineals, fins i tot problemes no lineals es linealitzen (es representen per un sistema d'equacions lineals en l'entorn d'un punt) i es resolen per iteracions successives on en cada iteració es resol un sistema d'equacions lineals. És a dir, en un cas senzill es té un sistema de la forma:

$\left\{{\begin{matrix}4x+2y&=&-1\\3x-y&=&2\end{matrix}}\right.$

i en el cas general, un sistema de la forma:

$\left\{{\begin{matrix}a_{1,1}.x_{1}+a_{1,2}.x_{2}+\cdots +a_{1,n}.x_{n}&=&b_{1}\\a_{2,1}.x_{1}+a_{2,2}.x_{2}+\cdots +a_{2,n}.x_{n}&=&b_{2}\\\vdots &&\vdots \\\vdots &&\vdots \\a_{m,1}.x_{1}+a_{m,2}.x_{2}+\cdots +a_{m,n}.x_{n}&=&b_{m}\end{matrix}}\right.$

Es pot citar com a exemple d'aplicació en arquitectura la resolució d'estructures articulades isostàtiques de barres unides entre elles en nusos. En carregar l'estructura es coneixen les càrregues aplicades i s'ha de calcular les reaccions en els suports i les tensions a les barres. Les barres només estan sotmeses a forces de tracció o de compressió (en estar articulades als nusos). L'estàtica imposa que la suma de forces a cada nus sigui zero. Això dona 3 equacions per a cada nus (una equació per cada una de les components x, y i z de les forces que hi apliquen les barres i de les forces exteriors aplicades al node) la tensió a què està sotmesa cada barra és una incògnita, i les reaccions en els suports també per tant hi ha tantes incògnites com barres més components desconegudes de les reaccions en els suports. Per exemple en el cas d'una gelosia plana triangular com la de la Figura 5 hi ha 6 equacions (les components z de les forces són totes zero en ser plana l'estructura) i 6 incògnites (3 per les tensions de cada barra i 3 per les reaccions en els suports).

El sistema d'equacions que en resulta és el següent:

Figura 5. Estructura de barres, es coneix la càrrega i cal determinar les reaccions en els suports i les tensions a les barres.

${\begin{aligned}T_{1}\sin \left(\alpha \right)+T_{2}\sin \left(\beta \right)&=F_{y}\\T_{1}\cos \left(\alpha \right)+T_{2}\cos \left(\beta \right)&=0\\R_{1y}-T_{1}\sin \left(\alpha \right)&=0\\-R_{1x}-T_{1}\cos \left(\alpha \right)-T_{3}&=0\\R_{2y}-T_{2}\sin \left(\beta \right)&=0\\T_{3}-T_{2}\cos \left(\beta \right)&=0\end{aligned}}$

Que en notació matricial s'escriu:

$\left({\begin{matrix}F_{y}\\0\\0\\0\\0\\0\\\end{matrix}}\right)=\left({\begin{matrix}\sin \left(\alpha \right)&\sin \left(\beta \right)&0&0&0&0\\\cos \left(\alpha \right)&\cos \left(\beta \right)&0&0&0&0\\-\sin \left(\alpha \right)&0&0&1&0&0\\-\cos \left(\alpha \right)&0&-1&0&-1&0\\0&-\sin \left(\beta \right)&0&0&0&1\\0&-\cos \left(\beta \right)&1&0&0&0\\\end{matrix}}\right)\cdot \left({\begin{matrix}T_{1}\\T_{2}\\T_{3}\\R_{1y}\\R_{1x}\\R_{2y}\\\end{matrix}}\right)$

Per altra banda si es pretén resoldre la cúpula geodèsica del museu Dalí de Figueres cal calcular un sistema amb 3276 equacions i 3276 incògnites (3270 tensions a les barres i 6 components de les reaccions en els suports).

La cúpula geodèsica del museu Dalí de Figueres és una estructura reticular formada per 3.270 barres.

Si bé és teòricament possible resoldre aquests sistemes d'equacions amb càlcul de determinants i de la matriu i de les matrius d'adjunts, aquest mètode no resulta factible a la pràctica per la quantitat d'operacions que requeriria. Porta ràpidament a una complexitat i una longitud de càlcul que no és ni de lluny tractable pels ordinadors més potents d'avui en dia. Això és particularment cert en casos d'estructures com la cúpula del museu Dalí de l'exemple.

Aquest problema es pot analitzar des d'un altre punt de vista. En primer lloc, el sistema d'equacions es pot considerat com la cerca d'un vector x, la imatge del qual per l'aplicació lineal u és igual a b.

Llavors u, x i b es poden descriure amb una matriu cada un i dos sistemes de coordenades:

$u:{\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}$ $x:{\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}$ $b:{\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}$

Llavors n'hi ha prou amb entendre bé l'aplicació u per resoldre de forma més senzilla la qüestió formulada. Es tracta de trobar un vector que en doni com a imatge per l'aplicació u el vector b. Aquesta aplicació és una aplicació lineal d'un conjunt en ell mateix. D'aquest tipus d'aplicacions sen diu endomorfismes. L'espai vectorial es descompon en subespais estables per u, és a dir que les seves imatges per u són incloses en ells mateixos. Així el problema se separa en un subproblema en cada un d'aquest subespais si són de dimensió 1 la solució és una simple divisió. Aquest subespais tenen propietats ben particulars. Entre tots generen l'espai vectorial sencer, però l'endomorfisme restringit a aquests subespais és particularment senzill. Un bon exemple bé donat pel cas del mirall. Sobre la superfície del mirall l'aplicació és senzilla: no modifica res; a la recta dels vectors perpendicular, l'aplicació té per a imatge, el vector oposat, i tot vector és la suma d'un component sobre el mirall i d'una perpendicular. Llavors trobar l'antiimatge de b un cop coneguda aquesta base és tan senzill com: expressar b en aquesta base (suma d'un vector en la superfície del mirall i un de la recta perpendicular al mirall) trobar les antiimatges d'aquests components (la del mirall no canvia i la perpendicular canvia de signe) i sumar-les.

Exemple numèric

Sigui una equació lineal la matriu de la qual és A (vegeu més avall). La resolució per inversió imposa càlculs llargs i complexos. Un enfocament basat en els valors i els vectors propis, la reduïda de Jordan, mostra que aquesta matriu, amb un canvi de base adequat es pot transformar en la matriu J:

$A=P.J.P^{-1}{\begin{pmatrix}5&4&2&1\\0&1&-1&-1\\-1&-1&3&0\\1&1&-1&2\end{pmatrix}}\;J={\begin{pmatrix}4&1&0&0\\0&4&0&0\\0&0&2&0\\0&0&0&1\end{pmatrix}}\;i\;P={\begin{pmatrix}-1&0&1&-1\\0&0&-1&1\\1&-1&0&0\\-1&1&1&0\end{pmatrix}}$

El problema, expressat inicialment sobre la matriu $A$ es transforma en un problema expressat amb la matriu $J$, i queda per tant molt simplificat. En aquest exemple, els valors propis de $A$ i de $J$ són els coeficients de la diagonal de $J$: 4,2,1; a cadascun d'aquests valors propis s'associa un subespai propi, en aquest cas tots són de dimensió 1 (en el cas general si els escalars són nombres reals els espais poden tenir com a màxim dimensió 2): la raó, en el cas dels valors 1 i 2, és que aquests coeficients no apareixen més que una vegada sobre la diagonal de $J$; per al valor 4, encara que aparegui dues vegades, la dimensió del subespai propi associat no poden ser 2, a causa de la presència del coeficient 1 sobre la diagonal, per tant es tracta de dos subespais de dimensió 1 i no d'un subespais de dimensió 2.

Cal dir que aquest problema, tot i ser el primer a aparèixer en àlgebra lineal, no va ser el que va obrir la via cap a la noció dels valors i vectors propis.

Mètode general de resolució en dinàmica

Sistema massa-oscil·lador: una massa oscil·lant unida a una molla.

Si amb el problema precedent no n'hi va haver prou per formalitzar la teoria dels vectors i valor propis, és essencialment a causa d'una absència de concepte de base. La geometria de llavors estava formalitzada pel concepte de punt. Els punts no se sumen, no posseeixen propietats algebraiques. La noció d'espai vectorial actual, no existia. Hamilton, el matemàtic anglès es va interessar per un problema on l'addició i la multiplicació escalar són naturals. Aquest problema prové de la física: els sistemes oscil·lants.

El cas de la figura il·lustra aquest problema. La massa s'uneix a una molla i experimenta un esmorteïment viscós (això vol dir que la força deguda als fregaments és proporcional a la velocitat). No existeix cap força exterior, i el sistema oscil·lant verifica l'equació diferencial lineal següent:

$(1)\quad M{\ddot {x}}+B{\dot {x}}+Kx\;=\;0$

Aquesta equació utilitza les derivades segones, és la raó per la qual se'n diu, una equació diferencial lineal de segon ordre. Tanmateix, és possible transformar una equació de segon, en un sistema de dues equacions de primer ordre afegint una nova variable, i per tant una nova dimensió a l'espai:

${\begin{aligned}&\left\{{\begin{matrix}M{\dot {v}}+Bv+Kx=0\\{\dot {x}}=v\\\end{matrix}}\right.\\&\left\{{\begin{matrix}{\dot {v}}=-{\frac {B}{M}}v-{\frac {K}{M}}x=0\\{\dot {x}}=v\\\end{matrix}}\right.\\&\left({\begin{matrix}{\dot {v}}\\{\dot {x}}\\\end{matrix}}\right)=\left({\begin{matrix}{\frac {-B}{M}}&{\frac {-K}{M}}\\1&0\\\end{matrix}}\right)\left({\begin{matrix}v\\x\\\end{matrix}}\right)\\\end{aligned}}$ Que fent

$\phi =\left({\begin{matrix}v\\x\\\end{matrix}}\right)\quad a=\left({\begin{matrix}{\frac {-B}{M}}&{\frac {-K}{M}}\\1&0\\\end{matrix}}\right)$ Queda

${\frac {d}{dt}}\phi =a\cdot \phi$

Si l'anàlisi del moviment comença per convenció a l'instant t₀ = 0, llavors:

$\phi \left(0\right)=\phi _{0}=\left({\begin{matrix}v_{0}\\x_{0}\\\end{matrix}}\right)$

Trajectòria de la massa oscil·lant

La solució d'aquesta equació és coneguda i s'escriu de la següent manera:

$\phi (t)=\exp(ta)(\phi _{0})\;$

La prova formal de què l'exponencial és la solució, es fàcil del veure, només cal derivar i comprovar que compleix la condició de contorn. Però la funció exponencial que apareix no és l'exponencial d'un nombre sinó la d'un endomorfisme (fixeu-vos que a és una matriu), l'expressió que permet definir aquesta exponencial es troba seguint un camí formalment idèntic al de trobar el desenvolupament en sèrie de Taylor de la funció exponencial real i resulta:

$\;\exp(ta)=\sum _{n=0}^{+\infty }{\frac {t^{n}a^{n}}{n!}}\;$

Vegeu funció exponencial d'una matriu Aquesta expressió depèn de totes les potències d'aquest endomorfisme. El problema de calcular-la el resol Hamilton gràcies a la noció de valors i vectors propis: en efecte, si existeix una base de vectors propis per a l'endomorfisme $a$, amb valors propis λ₁ i λ₂ i si A és l'a matriu de $a$; és a dir si existeix una matriu de canvi de base P tal que:

$A=P^{-1}{\begin{pmatrix}\lambda _{1}&0\\0&\lambda _{2}\end{pmatrix}}P\;$

llavors :

$\exp(tA)=\sum _{n=0}^{+\infty }{\frac {t^{n}P^{-1}A^{n}P}{n!}}=P^{-1}\left(\sum _{n=0}^{+\infty }{\frac {t^{n}}{n!}}{\begin{pmatrix}\lambda _{1}^{n}&0\\0&\lambda _{2}^{n}\end{pmatrix}}\right)P=P^{-1}{\begin{pmatrix}\ e^{\lambda _{1}t}&0\\0&e^{\lambda _{2}t}\end{pmatrix}}P\;$

La solució, tant per a la posició com per a la velocitat és doncs una combinació lineal d'exponencials.

Si existeixen dos valors propis reals, llavors la solució és del tipus de la que representa la corba blava de la figura. L'esmorteïment porta a la massa sense cap oscil·lació a la seva posició d'equilibri. Per contra, si no existeixen valors propis reals, cal trobar els complexos. La solució ve donada llavors per la part real de la matriu, i s'obté una trajectòria d'igual naturalesa que la corba vermella, amb oscil·lacions abans d'arribar al punt d'equilibri. La física és font de nombrosos exemples de problemes lineals de dimensió finita on els valors propis resulten el plantejament adequat per a la seva resolució. Se'ls troba per exemple en l'anàlisi dels circuits elèctrics.

Principi d'inèrcia de Sylvester

Formulació del principi d'inèrcia de Sylvester

Eixos dels moments principals d'inèrcia.

Sylvester analitza l'energia que s'ha de transmetre a un sòlid per donar-li una velocitat de rotació ω. Es fixa que el vector propi representa en aquest context un eix de rotació privilegiat, és a dir si s'aplica a l'objecte un parell de forces entorn d'un eix principal d'inèrcia, l'objecte gira entorn d'aquest eix, en canvi si el parell de forces s'aplica entorn d'un eix que no és un dels eixos principals d'inèrcia, llavors l'objecte gira entorn d'un eix diferent de l'eix entorn del qual se li està aplicant el parell. El valor propi correspon a la magnitud que en física es diu moment d'inèrcia, és inversament proporcional a l'energia que cal subministrar-li per obtenir una determinada velociat de rotació elevada al quadrat ($\omega ^{2}$).

$E={\frac {1}{2}}I\omega ^{2}\Leftrightarrow \omega ^{2}=2{\frac {E}{I}}$

Per obtenir una determinada velocitat angular amb la mínima energia, cal escollir l'eix que té el moment d'inèrcia més petit. La teoria demostra que l'eix on el moment principal d'inèrcia és més gran és sempre perpendicular a aquell on és més petit. Aquesta perpendicularitat correspon a l'existència d'una base ortonormal de vectors propis.

El cas de l'escombra de la figura, il·lustra un exemple d'aquest fenomen. L'eix principal amb el moment d'inèrcia més petit és l'eix vertical indicat per la fletxa 1. És intuïtiu que l'energia necessària per obtenir la mateixa velocitat de rotació segons l'eix de la fletxa 2 serà molt superior. Els vectors propis i els valors propis apareixen com a característiques pròpies de la geometria de l'objecte, en aquest cas els eixos privilegiats de rotació. En aquest cas els valors propis són sempre reals perquè el tensor d'inèrcia és simètric.

Un enfocament similar s'aplica en mecànica dels medis continus per a l'anàlisi de les tensions i les deformacions elàstiques els tensor tensió i tensor deformació són també simètrics i per tant els valors propis són també reals. En aquest cas els valors propis corresponen a les direccions on l'estat de tensió correspon a una compressió (o una tracció) pura sense esforç tallant.

Aplicació en estadística

Article principal: anàlisi de components principals

L'enfocament de Sylvester es fa servir en nombrosos àmbits per comprendre la geometria d'un fenomen. Les tècniques estadístiques d'anàlisi d'enquestes en són un perfecte exemple. Si una enquesta sobre una mostra de cent persones conté sis criteris. Si es pot avaluar cada pregunta per un criteri numèric, llavors les respostes es poden interpretar com a punts en un espai de dimensió 6 i es factible una anàlisi dels components principals. Això permet interpretar els resultats de l'enquesta.

Primer es normalitzen els resultats de l'enquesta multiplicant el resultats per una factor de forma que un criteri que, per exemple, pren valors entre un i cent no sigui deu vegades més important que un altre que pren valors d'u a deu. Llavors el resultat de l'enquesta es considera com un sòlid en un espai de tantes dimensions com preguntes.

Resultat d'una enquesta

Anàlisi ACP. L'eix principal es el més explicatiu explicatiu.	Exemple de dues preguntes amb respostes correlacionades.	Exemple de dues preguntes amb respostes no correlacionades.

La primera figura representa l'ACP sobre els dos primers vectors propis, que es diuen en estadística components principals. Els valors es reuneixen al voltant d'aquest eix, el que significa que és el més explicatiu. Aquest caràcter explicatiu ve donat pel quadrat del valor propi. En l'exemple, és a causa de dos criteris fortament correlacionats. Aquest fenomen es veu a la segona figura on es representen els dos criteris correlacionats. Aquests criteris es reuneixen al voltant d'una recta, en l'exemple aquesta recta és la recta del component principal (aquell valor propi més gran). Si els criteris són ingressos i sobrepès, llavors l'enquesta indica que l'obesitat colpeix prioritàriament la gent amb ingressos més febles. La tercera figura il·lustra un cas, on la correlació entre els dos criteris és feble. Si els criteris són talla i nivell d'estudis, llavors el gràfic indica que la talla no és un criteri correlacionat amb el nivell d'estudis.

Aquests exemples il·lustren que, els valors i vectors propis no són només eines de càlcul abstracte, sinó elements constitutius de la geometria del problema.

Aplicació en relativitat

El principi d'inèrcia de Sylvester en relativitat

Article principal: Relativitat especial

A partir dels moments d'inèrcia d'un sòlid, Sylvester va més enllà, no es va equivocar pas en el títol del seu article de 1852 Teoria dels invariants algebraics. Els valors propis, que són els invariants, superen de lluny el marc dels moments d'inèrcia. La geometria de l'espaitemps relativista n'és un exemple. Aquí la forma bilineal ja no descriu el moment d'inèrcia d'un sòlid rígid, sinó una modelització de la geometria pròpia i tot del nostre univers.

La transformació de Lorentz s'aplica a la relativitat especial i permet calcular la posició i el temps en què un observador detecta un fet puntual a partir de les dades de la posició i el temps en què ha detectat aquest mateix fet puntual un altre observador. Aquesta transformació, per cada velocitat relativa entre els dos observadors és una aplicació lineal. L'expressió matemàtica que adopta aquesta aplicació lineal és la següent:

$\left({\begin{matrix}{{x}'}\\{{t}'}\\\end{matrix}}\right)={\frac {1}{\sqrt {1-{}^{v^{2}}\!\!\diagup \!\!{}_{c^{2}}\;}}}\left({\begin{matrix}1&-v\\{\frac {-v}{c^{2}}}&1\\\end{matrix}}\right)\left({\begin{matrix}x\\t\\\end{matrix}}\right)$

On x, i t són la posició i el temps mesurats pel primer observador i x’ i t’ són els mesurats pel segon, v és la velocitat del segon observador respecte del primer i c és la velocitat de la llum. Aquesta equació parteix de la hipòtesi que els orígens dels sistemes de coordenades dels dos observadors coincideixen (en l'instant inicial t=t’=0 el punt de x=0 coincideix amb el punt x’=0) En aquesta equació, l'espai i el temps tenen un paper que no és simètric, si es fa el canvi de coordenades:

$t_{m}=ict\quad {t}'_{m}=ict'$

On i és ${\sqrt {-1}}$, l'aplicació adopta una forma especialment simètrica:

$\left({\begin{matrix}{{x}'}\\{t}'_{m}\\\end{matrix}}\right)=\left({\begin{matrix}{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}&{\sqrt {\frac {-v^{2}}{c^{2}-v^{2}}}}\\{\sqrt {\frac {-v^{2}}{c^{2}-v^{2}}}}&{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}\\\end{matrix}}\right)\left({\begin{matrix}x\\t_{m}\\\end{matrix}}\right)$

Fixeu-vos que si no s'afegeix el component i al canvi de variables les velocitats v al quadrat queden positives al numerador i negatives al denominador, no assolin-se la simetria que es busca. Amb aquest canvi de variables l'espai es diu espai de Minkowski. La figura representa aquesta geometria. En aquest espai existeix un eix particular, on el quadrat de la distància posseeix una propietat especial: és negatiu. La distància d'aquesta teoria no és sempre positiva. Un vector de coordenades (x, y,z, t) té per mòdul x²+y²+z²-c².t². Hermann Minkowski 1864-1909 desenvolupa un sistema matemàtic basat en aquests principis el 1907 en un article titulat Espaitemps, i l'aplica a la relativitat l'any següent.

El con d'inèrcia de la figura representa l'univers per a un observador en el punt A. El punt C està a una distància negativa, per arribar-hi caldria una velocitat superior a la de la llum, lo que, en el context d'aquesta teoria no és realitzable. És doncs inobservable i no pot tenir cap influència directa o indirecta sobre l'observador. El punt B és en el qual es diu el con de llum, és un punt possible, podrà interaccionar amb l'observador (enviant o rebent senyals a la velocitat de la llum).

En el cas que interessa Minkowski, els endomorfismes que tradueixen les lleis físiques d'un observador a un altre observador, tenen un paper important; són els que verifiquen l'equació $<u(x),u(y)>=<x,y>$, on $<,>$ és la forma bilineal que descriu la geometria considerada. Aquests endomorfismes deixen la geometria invariant, corresponen en una modelització euclidiana a les isometries. En la geometria de la relativitat, 1 és valor propi i el seu espai propi associat és de dimensió 3 i i.c és un valor propi amb subespai propi associat de dimensió 1, on i designa el nombre imaginari i c la celeritat de la llum. Es parla de signatura de Sylvester (3,1). Totes les lleis físiques han de ser invariants per aquests endomorfismes. Aquests endomorfismes formen una estructura de grup, anomenat grup especial unitari, la relativitat torna a escriure la física en lleis que resulten invariants pel grup especial unitari de dimensió 4 i de signatura (3,1).

Representació dels grups

Exemple d'aplicació lineal: una simetria respecte a l'eix horitzontal central

L'anàlisi emprant vectors i valors propis també té com a àmbit d'aplicació la representació dels grups. Una estructura de grup és una de les que té una definició algebraica més simple, és un conjunt proveït d'una sola operació notada sovint com la multiplicació. Si bé la definició és senzilla, per contra, aquestes estructures resulten de vegades prou complexes perquè la seva teoria encara no sigui coneguda del tot. Com a exemple de grup, és possible citar el de les rotacions del cub que la seva superfície invariant. La figura mostra que aquest grup és generat per tres permutacions, la que col·loca la cara 1 en posició 2, representada amb la fletxa vermella, la representada amb la verda i finalment la blava. En total aquest grup implica 24 elements. Una representació d'un grup consisteix a una identificació dels seus elements amb endomorfismes de tal manera al que l'operació del grup correspongui a la composició d'endomorfisme. Així en l'exemple de la figura, existeix una identificació natural entre el grup abstret de les 24 rotacions del cub amb un grup de rotacions en un espai de dimensió 3.

Aquest enfocament permet llavors disposar de les eines com els vectors o valors propis per a l'anàlisi de l'estructura dels grups. La teoria mostra que els espais propis d'una representació corresponen a la part commutativa del grup. En el cas d'un grup completament commutatiu, existeix una base de vectors propis per a tota la representació. Aquest enfocament demostra, per exemple que els grups commutatius finits són productes de cicles.

La representació dels grups finits (és a dir que tenen un nombre finit d'elements) té un paper important en la teoria dels vectors propis. Ha permès a Jordan, en un context relativament general, comprendre totalment el camp d'aplicació i els límits d'un enfocament per vectors propis. Llavors queden clares les condicions necessàries i suficients d'existència de vectors propis o de bases de vectors propis. A més, s'identifiquen els casos on no existeix base de vectors propis així com l'estructura exacta dels endomorfismes que entren en aquesta categoria i la proporció d'endomorfismes d'aquesta naturalesa en el total d'endomorfismes.

Si bé el context és relativament general, no cobreix pas tots els casos d'espais vectorials coneguts. La teoria de Jordan es limita als de dimensió finita amb un cos de nombres algebraicament tancat. Un cos s'anomena algebraicament tancat si tots els seus polinomis tenen almenys una arrel. Aquest context és no obstant això prou general per cobrir totes les aplicacions citades en aquest capítol.

Teoria en dimensió finita

Enfocament elemental

Article principal: Polinomi característic

Una primera observació que simplifica l'estudi. Si λ és un valor propi d'un endomorfisme u, llavors un vector propi p és un vector no nul que té per imatge λu, per tant:

${\begin{aligned}&u\left(p\right)=\lambda p\\&u\left(p\right)-\lambda p=0\\&u\left(p\right)-\left(\lambda I\right)\left(p\right)=0\\&\left(u-\lambda I\right)\left(p\right)=0\\\end{aligned}}$

On I és l'endomorfisme identitat.

Per tant, l'espai propi associat a λ és el conjunt dels vectors que tenen imatge 0 per aquesta aplicació. Aquest conjunt es diu que és el nucli de l'endomorfisme $u-\lambda I$. Les propietats generals estableixen que aquest conjunt és un subespai vectorial.

Una funció important, en particular en aquest marc, és la funció determinant que associa a cada endomorfisme un nombre. El seu interès resideix sobretot en el fet que el determinant d'un endomorfisme és nul si i només si existeixen vectors no nuls que tenen per a imatge el vector nul per aquest endomorfisme, és a dir si i només si 0 és un valor propi per a aquest endomorfisme. El determinant de l'aplicació $u-\lambda I$ es diu el polinomi característic. Aquestes observacions subministren a les propietats:

• Sigui λ un valor propi, llavors l'espai propi de valor propi λ és el subespai vectorial igual al nucli de $u-\lambda I$,
• un espai propi és un subespai vectorial
• les arrels del polinomi característic són els valors propis.

Aquesta última propietat mostra que l'existència d'arrels de polinomis té influència sobre la teoria dels valors propis. De fet, l'existència dels valors propis depèn de l'existència d'arrels del polinomi característic. És per això què en el marc del cos dels nombres complexos, que està algebraicament tancat segons el Teorema fonamental de l'àlgebra, les propietats vinculades als valors propis s'estudien de forma més simple que en el marc del cos dels reals.

Propietats suplementàries

:* Els espais propis E_i de valors propisλ_i formen una suma directa de subespais vectorials estables per u.

Aquesta propietat es demostra simplement amb les eines desenvolupades a l'article Polinomi d'endomorfisme. X - λ_i és un polinomi anul·lador de la restricció de u à E_i.

• Tota família de p. vectors propis de u associats a valors propis dos a dues diferents és una família lliure.

Aquesta propietat és un corol·lari directe de la proposició precedent.

• Si dos endomorfismes u i v commuten, llavors un espai propi de u és estable per v.

Sigui x un vector propi de u, de valor propi λ, llavors:

$u\circ v(x)\;=\;v\circ u(x)\;=\;\lambda v(x)$ Això demostra que v(x) ja sigui nul ja sigui un vector propi de valor propi λ és un element de l'espai propi de x.

Cas on l'endomorfisme és diagonalitzable

Article principal: Matriu diagonalitzable

Modificació d'un paral·lelòtop els costats del qual formen una base de vectors propis per un endomorfisme diagonalitzable.

El concepte de l'article és particularment clar en el cas on el comportament de l'endomorfisme queda descrit completament pels vectors i valors propis. Llavors es diu que l'endomorfisme és diagonalitzable.

Un endomorfisme és diagonalitzable si i només si existeix una base de vectors propis.

És el cas del primer exemple, el del mirall. Es pot escollir una base prenent dos vectors lliures en el pla del mirall i un tercer de perpendicular a aquest pla. Els dos primers vectors tenen per a imatges ells mateixos i són doncs de valor propi 1 i l'últim és de valor propi -1. Aquesta situació és interessant per tres motius: correspon a un cas simple de tractar, és sota certes hipòtesis freqüent, finalment existeix en múltiples criteris per identificar-lo.

• La simplicitat d'aquesta situació prové de dos fets. Existeix una descomposició de l'espai en subespais estables, senzills en si mateixos, i sobre la qual l'endomorfisme és senzill de descriure. Aquests subespais són senzills, ja que són de dimensió 1: són rectes. La linealitat de l'endomorfisme permet conèixer exhaustivament el comportament de la transformació, una vegada es compren el comportament sobre aquestes rectes. Finalment la restricció de l'endomorfisme a aquestes rectes és una homotècia, és a dir una dilatació (o contracció), d'un factor el valor propi. Un exemple d'aquesta situació és el donat a la figura: un paral·lelòtop groc les arestes del qual són la base de vectors propis, la imatge per l'endomorfisme és un paral·lelòtop les arestes del qual han conservat les mateixes direccions, però les seves longituds han estat modificades.

Aquesta simplicitat obre la via a nombroses aplicacions evocades anteriorment a l'article. Permet per exemple el càlcul d'una exponencial d'endomorfisme i per tant la resolució de nombrosos problemes mecànics.

Superfície que representa l'adherència sobre el cos dels complexos dels endomorfismes no diagonalitzables.

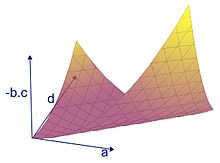
• Aquesta situació és força freqüent. La figura de la dreta és una il·lustració del cas on l'espai vectorial és de dimensió 2 sobre els nombres reals. El conjunt dels endomorfismes és llavors un espai de dimensió 4: tot endomorfisme admet una representació matricial de la forma ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$. Per poder obtenir una representació gràfica de dimensió 3, els coeficients b i c de la matriu s'han representat conjuntament a l'eix vertical a través del valor -b.c. Utilitzant els criteris de diagonalitzabilitat, es comprova que hi ha una superfície particular, de dimensió 2, que és la que apareix en aquesta representació (seria de dimensió 3, si es pogués representar tot en l'espai, de dimensió 4, dels endomorfismes). Aquesta superfícies correspon a una situació límit per a la diagonalitzabilitat: la zona de fora de la superfície conté els endomorfismes diagonalitzables, la zona de sobre conté dels endomorfismes diagonalitzables només sobre els nombres complexos. En la representació escollida, els endomorfismes diagonalitzables sobre els nombres complexos ocupen doncs gairebé tot l'espai; és en aquest sentit que el cas de diagonalitzabilitat és freqüent. Per contra els endomorfismes que són diagonalitzables fins i tot sobre els reals n'ocupen essencialment la meitat. Aquesta situació de freqüència s'ha de posar en relació amb la situació dels polinomis de coeficients reals, dels quals les arrels o bé reals, o bé només complexes. Hi ha un cas particular a la zona dels endomorfismes diagonalitzables només sobre els nombres complexos: les rotacions, de les quals s'ha donat l'exemple de la rotació de la Terra sobre ella mateixa. Finalment, pel que fa a la superfñície mateixa, hi ha dos tipus de situacions. La recta horitzontal d'equació a = d amb b = c = 0 representa la recta de les homotècies, del mateix tipus que el segon exemple de l'article. Els altres punts de la superfície representen els únics endomorfismes no diagonalitzables.
• Finalment existeixen múltiples criteris per caracteritzar un endomorfisme diagonalitzable. Un primer enfocament consisteix en estudiar el polinomi característic. Una altra d'àmpliament més sofisticat consisteix en estudiar els polinomis de l'endomorfisme. Llavors un dels conceptes clau és polinomi mínim que subministra, per exemple, a un criteri diagonalització particularment senzill.

Els criteris associats a la diagonalització es donen a la següent caixa desplegable.

Propietats suplementàries

Les següents proposicions són equivalents:

• L'endomorfisme és diagonalitzable
• Existeix una base de vector propi
• La suma dels espais propis engendra l'espai sencer
• La suma de les dimensions dels espais propis és igual a la dimensió de l'espai sencer
• Tota representació matricial de u és diagonalitzable.

En el cas complex (és a dir on el cos de nombres és el dels complexos) aquesta propietat es compleix quasi per a tot en el sentit de la mesura. En el sentit de la topologia els endomorfismes diagonalitzables són densos.

Demostracions a Diagonalització d'endomorfismes.

• Les arrels del polinomi mínim formen el conjunt dels valors propis.

Demostració a Valor propi (síntesi)

• Un endomorfisme u és diagonalitzable si i només el seu polinomi mínim es descompon sobre K i en arrels simples.

Demostració a Polinomi d'endomorfisme

• Si existeixen n valors propis diferents llavors l'endomorfisme és diagonalitzable.

Demostració a Valor propi (síntesi)

• Si l'endomorfisme és diagonalitzable, llavors el polinomi característic es descompon en producte de monomis.

Demostració a Reducció d'endomorfismes

L'ordre de multiplicitat algebraica d'un valor propi és l'ordre de multiplicitat de l'arrel del polinomi característic. L'ordre de multiplicitat algebraica d'un valor propi correspon doncs a la potència del monomi (X-λ) en el polinomi característic. Aquesta definició permet expressar d'una condició necessària i suficient de diagonalitzabilitat.

• L'endomorfisme és diagonalitzable si i només si, tot espai propi posseeix una dimensió igual a la multiplicitat algebraica del valor propi associat.

Demostració a Reducció d'endomorfismes

Cas Complex

Exemple d'imatge d'una base per un endomorfisme nilpotent en dimensió 3.

Article principal: Forma canònica de Jordan

La figura de la dreta mostra que, fins i tot en el cas on el cos és el dels nombres complexos, queden encara casos per estudiar, el dels endomorfismes que se situen sobre la superfície, però no a la dreta de les homotècies. En el cas dels sistemes d'equacions diferencials lineals, no intervé més que com un cas límit, en l'enfocament de Sylvester, no apareix mai. Per contra en la teoria dels grups, aquest cas és important. Aquest tipus d'endomorfisme permet la representació dels grups no commutatius. Si aquests grups són infinitament diferenciables, llavors permeten la representació d'un cas important, el dels grups de Lie nilpotents.

Per estudiar aquesta problemàtica, els mètodes utilitzats són els que va posar a punt en Nelson Dunford. L'eina essencial consisteix a considerar les combinacions lineals de potències de l'endomorfisme. S'obté així un polinomi de l'endomorfisme. Aquests polinomis formen una estructura d'àlgebra commutativa dotat d'un morfisme del conjunt dels polinomis cap a aquesta àlgebra. Aquest enfocament és prolific, es troba també en l'estudi del cas on la dimensió no és finita. La teoria associada a aquest enfocament es troba a l'article Polinomi d'endomorfisme, i l'aplicació al cas tractat aquí en Descomposició de Dunford.

El resultat destacable és que no existeix en aquest context més que una única excepció estructural al cas diagonalitzable. És el cas on l'endomorfisme u a la potència p, on p és un enter, és igual a 0. Es diu llavors que l'endomorfisme és nilpotent. Es pot considerar per exemple en dimensió 3, si (e₁, e₂, e₃,) és una base l'endomorfisme que verifica u(e₁)=e₂, u(e₂)=e₃ i u(e₃)=0. Aquest endomorfisme clarament és no nul i el seu polinomi característic és igual a x3 per tant l'únic valor propi és 0. Aquest exemple s'il·lustra en figura.

Camille Jordan ha demostrat que en aquest context, tot endomorfisme és suma d'un endomorfisme diagonalitzable i d'un endomorfisme nilpotent i que commuten entre ells. L'aplicació de la teoria dels endomorfismes mostra que el cas nilpotent disposa d'una representació matricial particularment simple i triangular superior. En el cas general, aquesta representació es diu la reduïda de Jordan, demostra també que, en aquest cas, tota matriu és semblant a una matriu triangular.

Propietats suplementàries

:* Tot endomorfisme u és la suma d'un endomorfisme diagonalitzable i d'un endomorfisme nilpotent que commuten entre ells.

Demostració a Polinomi d'endomorfisme

• Tota matriu de u si és triangularitzable, admet una representació de Jordan.

Demostració a Forma canònica de Jordan

La noció d'espai característic generalitza l'espai propi. Correspon al nucli de l'endomorfisme (u - λ.Id)ⁿ. Les següents propietats es demostren a l'article Descomposició de Dunford

• L'espai E és suma directa dels seus subespais característics.
• Els subespais característics no es redueixen al vector nul i els vectors estables per l'endomorfisme. La restricció de l'endomorfisme en l'espai propi associat al valor propi λ és la suma d'una homotècia de raó λ i d'un endomorfisme nilpotent.
• Un espai propi està inclòs en l'espai característic d'igual valor propi.
• La família de projeccions sobre els espais característics així com els endomorfismes diagonalitzables i nilpotents s'expressen en forma de polinomis d'endomorfisme de u.
• El polinomi mínim és el producte dels polinomis de grau 1 i d'arrel els valors propis de la potència índex de l'endomorfisme nilpotent associat.
• El polinomi característic és el producte dels polinomis de grau 1 i d'arrel els valors propis de la potència la dimensió de l'espai característic associat.
• El determinant és igual al producte dels valors propis elevats a la potència de la dimensió de l'espai característic associat.
• La traça és igual a la suma dels valors propis multiplicats per la dimensió de l'espai característic associat.

Cas Real

Rotació de la terra.

Sobre els reals un polinomi no sempre admet arrel. En el tercer exemple, el de la rotació de la terra, l'espai és de dimensió 3, ara bé tot polinomi del tercer grau posseeix una arrel sobre els reals. En conseqüència, existeix almenys una recta de vectors propis. És l'eix dels pols en l'exemple. Per contra, en el cas de dimensió parella, per exemple la restricció d'aquesta aplicació al pla il·lustrat en blau sobre la figura de l'equador, l'existència de valor propi ja no està garantida. Aquí, una anàlisi geomètrica mostra que és en va buscar un vector propi, ja que la rotació modifica la direcció de tots els vectors no nuls.

En el cas complex, s'ha vist que només un terme nilpotent pot prohibir la diagonalització. En el cas real, una vegada retallat el terme nilpotent, sol les rotacions impedeixen la diagonalització. Existeixen llavors dues maneres de reduir el cas real. La primera solució consisteix a submergir l'endomorfisme a un espai vectorial complex. És la solució la més senzilla i la més freqüent. La reducció de l'endomorfisme és llavors més fàcil. Una vegada realitzada aquesta reducció, l'aplicació d'aquesta reducció a vectors reals donen sempre les solucions reals.

La segona solució consisteix en debilitar la reducció. Tot endomorfisme sobre els nombres reals és la suma del producte d'un endomorfisme diagonalitzable i d'una rotació amb un endomorfisme nilpotent. L'endomorfisme diagonalitzable commuta amb l'aplicació nilpotente i la rotació. Per contra, l'aplicació nilpotent no commuta amb la rotació. Demostració en Reducció d'endomorfisme

Cas d'un Mòdul sobre un anell

Les definicions no utilitzen pas el fet que $\mathbb {K}$ sigui un cos. Aquestes definicions tenen doncs sentit també en el cas on E no és un espai vectorial sinó un Mòdul sobre un anell. Si l'anell no és commutatiu, es parlarà llavors de valor propi a la dreta (la imatge del vector és el vector multiplicat pel valor propi) o de valor propi à l'esquerra (la imatge del vector és el valor propi multiplicat pel vector). Si l'anell és commutatiu es parlarà simplement de valor propi (perquè tant si es multiplica el vector pel valor com el valor pel vector el resultat obtingut és sempre el mateix).

Cas de les formes bilineals

Article associat: Teorema espectral

La imatge d'una esfera per un endomorfisme autoadjunt

Els endomorfismes també es fan servir per a representar formes bilineals, que són objectes d'igual naturalesa que les distàncies euclidianes. Els valors i vectors propis prenen en aquest context un significat particular.

Les formes bilineals són funcions que no són lineals, sinó quadràtiques, en el sentit que la funció ja no s'expressa com una combinació lineal de les coordenades, és a dir un polinomi (de diverses variables) de grau 1 en les coordenades, sinó com un polinomi del segon grau en les coordenades. La distància euclidiana sobre l'espai $\mathbb {R} ^{3}$ per exemple, s'obté a partir de la forma bilineal en la qual efectivament intervé un polinomi de grau 2.

Hi ha certes propietats que de vegades tenen les formes bilineals, com per exemple la simetria, que si es dona el cas les fan més fàcils d'estudiar. La distància euclidiana per exemple és simètrica, així la distància d'un punt a en un punt b és la mateixa que la distància d'un punt 'b a un punt a. Un endomorfisme que representa una forma bilineal simètrica s'anomena autoadjunt.

Aquests endomorfismes autoadjunts disposen, de fet, de propietats fortes en relació amb valors i vectors propis: no només admeten vectors propis, sinó que a més amb aquests n'hi ha prou per comprendre completament l'endomorfisme; un endomorfisme autoadjunt és diagonalitzable. Llavors, els vectors propis es poden escollir amb una propietat forta: existeix una base ortonormal de vectors propis. Finalment, per a aquest cas particular, existeixen mètodes de càlcul senzills i ràpids per obtenir els valors i vectors propis. Aquesta situació s'il·lustra gràficament a la figura. Un endomorfisme autoadjunt transforma la bola unitat en un el·lipsoide del qual els eixos en són els vectors propis i les longituds dels semieixos els valors absoluts dels valors propis.

D'altra banda, la forma bilineal inicial descriu aquí l'equivalent a una distància d'un espai geomètric; l'espai estudiat, proveït de la forma bilineal, és un nou espai geomètric. Sylvester mostra que els vectors i valors propis, de l'endomorfisme autoadjunt associat, són invariants, dels ens que descriuen les grandàries naturals i característiques de la geometria considerada. El significat físic d'aquestes grandàries depèn del context de l'espai estudiat. Sylvester va aplicar el que precedeix al principi d'inèrcia d'un sòlid rígid en mecànica i en va deduir l'existència d'eixos de rotació (vectors propis) i de moment principals d'inèrcia (valors propis) intrínsecs del sòlid. Els altres exemples d'aplicacions mostren que n'hi ha igualment en altres situacions, per exemple en estadística on els components principals revelen la dimensió més significativa d'una enquesta, o la relativitat que mostra l'existència d'un invariant, la signatura de Sylvester, en l'estructura fins i tot de la geometria del nostre univers.

Així, el paper dels vectors i valors propis es veu modificat. Ja no són només eines de càlcul necessàries per accelerar un algorisme o per resoldre un problema tècnic solucionant una equació diferencial, adquireixen autonomia pròpia, i resulten els invariants constitutius d'una geometria. Prenen llavors noms específics en cada àmbit d'aplicació; es parla per exemple d'eix de rotació en mecànica, de components principals en estadístiques, o de direccions pròpies en el cas d'espais corbats.

La demostració de l'existència d'una base de vectors propis en el cas dels endomorfismes autoadjunts es dona a l'article Diagonalització.

Teoria espectral

Posicionament del problema

L'anàlisi del cas de la dimensió finita mostra que el coneixement dels valors propis i dels espais de Jordan associats permet una comprensió profunda dels endomorfismes. És doncs natural intentar estendre aquest enfocament als casos d'espais vectorials de dimensions no finites (normalment espais de funcions que s'estudien en el marc dels espais de Hilbert.

Aquesta necessitat de generalització apareix de manera natural en matemàtiques. Els espais esdevenen espais de funcions on els endomorfismes els operadors diferencials, com les derivades els gradients o les laplacianes. L'exemple de la corda vibrant és característic d'un enfocament d'aquesta naturalesa. En aquest context el vocabulari evoluciona, ja no es parla d'endomorfisme sinó d'operador, es fa servir el terme de funció pròpia per designar un vector propi. Aquest pas pren el nom de teoria espectral. És una branca del que es diu l'anàlisi funcional.

L'enfocament espectral és atractiu per molts aspectes. Analitzar no només les propietats analítiques de les eventuals solucions, sinó també fins i tot la naturalesa de l'espai geomètric és un enfocament elegant. Ofereix eines noves, com ara bases o distàncies per resoldre dificultats sovint complexes. En el cas de la dimensió finita, aquest enfocament aporta teoremes potents, alhora teòrics i algorísmics. Joseph Fourier, mostra que això també passa de vegades en casos més generals, amb l'estudi de l'equació de la calor o de les cordes vibrants. David Hilbert confirma l'encert d'aquest camí obrint la via a una teoria espectral general.

Dificultats de l'enfocament

Les propietats geomètriques dels espais de funcions són per desgràcia molt més febles que en el cas de dimensió finita. La primera diferència és la presència d'una base en el sentit algebraic de la paraula. En general, no és possible construir una família lliure i generadora de l'espai per combinació lineal finita. Existeixen contraexemples com l'espai vectorial dels polinomis. Però aquest espai és massa estret per contenir moltes solucions de les equacions que s'intenta resoldre. Per exemple, la posició inicial d'una corda de guitarra pinçada pel músic té molt poques oportunitats de ser en l'univers dels polinomis trigonomètrics.

Aquest tipus d'espai es pot generalitzar per obtenir una bona completesa. Llavors s'obté l'espai de les sèries trigonomètriques o el de les sèries enteres. Llavors els resultats són bons candidats per establir els fonaments d'una teoria espectral. Per comprendre la geometria d'aquests espais, és essencial la topologia. En efecte, per construcció de l'espai, les solucions apareixen com a límits de successions. Tanmateix la topologia amaga moltes sorpreses per als espais funcionals.

En dimensió finita, totes les normes defineixen la mateixa topologia. De fet, no existeix veritablement més que una topologia interessant per a una anàlisi en vectors propis. En dimensió infinita, ja no és el cas, la topologia feble per exemple no posseeix ni tan sols cap distància associada.

En dimensió finita, la compacitat és sempre certa per als subconjunts tancats i fitats. El teorema de Riesz indica que aquest no és mai el cas si la dimensió no és finita. En el cas general es fa il·lusori voler extreure subsuccessions convergents per a trobar vectors propis.

Un endomorfisme és sempre continu en dimensió finita. No és el cas per als operadors lineals dels espais funcionals. La derivada, per exemple, no posseeix aquesta propietat. Per assegurar-se'n, n'hi ha prou amb considerar la successió de monomis $(x^{n})\;$. Sobre l'interval [0,1], és fitada. Ara bé la imatge de la successió per la funció derivada ja no posseeix aquesta propietat. En el cas general, un operador lineal és continu si i només si la imatge de la bola unitat és fitada, aquesta és la raó per la qual es parla més sovint d'operador fitat que d'operador lineal continu.

Espectre i conjunt de valors propis

Article principal: Espectre (anàlisi funcional)

En dimensió finita, si un endomorfisme a és suprajectiu llavors és bijectiu. Així, l'aplicació a - λIés una bijecció si i només si λ no és pas un valor propi. Això no és cert en el cas general. Considerant per exemple E l'espai de les funcions infinitament derivables sobre l'interval [0,1], i considerant l'operador A, que, a la funció f(x), li associa la funció xf(x). És relativament senzill comprovar que és fitat i no posseeix valor propi. Es considera l'operador A - λI que, a la funció f(x), li associa la funció f(x)(x-λ). Si està comprès entre 0 i 1, llavors no és suprajectiu, ja que la seva imatge no conté les funcions tals que la imatge de λ és diferent de 0. Es parla llavors d'espectre per donar compte d'aquest fenomen. L'espectre conté sempre el conjunt dels valors propis, i en dimensió finita, aquestes dues nocions coincideixen. En aquest exemple l'espectre és l'interval [0,1] i el conjunt dels valors propis és buit.

La definició precisa de l'espectre és la següent: Sigui E un espai de Banach i O un operador lineal, llavors l'espectre és el conjunt dels escalars tal com l'operador O - λI no admet recíproc. Segons el context, és possible afegir com a condició la continuïtat de l'invers.

Cas de la dimensió qualsevol:

Un espai vectorial E sobre K s'anomena K_variant si es pot trobar un endomorfisme (llavors anomenat K_variant per a E) que no deixa estable cap subespai finit i que no posseeix, a fortiori, cap vector propi.

Aquest espai habitualment també s'anomena Espai de Baire-Amofrãn.

Observació: Un espai que no és K_variant s'anomena K_invariant. Tot espai de dimensió finita sobre un cos algebraicament tancat és K_invariant (el polinomi característic es descompon sobre K!). R[X] en canvi es torna K_variant per l'endomorfisme canònic d'Amofrãn P->X*P.

Es diu família de K_variància o família de Brenef una família lliure d'endomorfismes K_variant per a E. El teorema de Baire-Brenef diu que mentre que E és complet si la bola tancada per a la topologia induïda sobre l'espai de variància (engendrat per una família de Brenef) és compacta. En efecte, el Lema de Chabran assegura que l'espai de variància és de dimensió enumerable, i això sigui quin sigui el cos.

Un espai K_invariant s'anomena totalment invariant sobre K si l'espectre de tot endomorfisme K_invariant per E és un convex tancat de K.

Descomposició espectral dels operadors autoadjunts compactes

En dimensió finita, el paràgraf sobre l'àlgebra bilineal explica ensenya que existeix un cas on és possible trobar una base de vectors propis sense utilitzar els polinomis d'endomorfismes. És un bon marc per a una generalització, ja que la noció de polinomi s'aplica malament en el cas dels espais funcionals. Per seguir aquest camí, a l'espai cal afegir-li una distància, euclidiana o hermitiana i l'endomorfisme posseeix sempre la bona simetria que es diu autoadjunta. En aquest context, la bola unitat es transforma en un el·lipsoide com el representat a la figura de les formes bilineals. Els eixos principals d'aquest el·lipsoide són els vectors propis i les longituds d'aquests semieixos són els valors propis. Aquest enfocament geomètric guia a David Hilbert per establir un resultat important de teoria espectral, en el cas de la dimensió infinita.

L'espai vectorial posseeix una distància euclidiana o hermitiana. En el cas general, és necessari afegir la completesa i la separabilitat. Aquest tipus d'espai s'anomena un espai Hilbert separable. Les sèries trigonomètriques o les funcions definides sobre un segment en el qual, el quadrat d'aquestes funcions és integrable, corresponen a aquest tipus d'espai. És també el marc que es fa servir en aquest paràgraf.

L'operador posseeix una bona simetria. Continua sent la mateixa que la de la dimensió finita, aquest operador és aquí autoadjunt.

Finalment l'operador disposa d'una bona propietat de continuïtat. Amb el fet que sigui fitat ja no n'hi ha prou. És compacte, això significa que la imatge de la bola unitat és compacta. Una de les conseqüències és que ja no és invertible.

En aquest context, s'estableixen resultats anàlegs a la dimensió finita. Per exemple:

• En un espai de Hilbert, un operador autoadjunt compacte posseeix un espectre compacte que conté sempre el valor 0.

• En un espai de Hilbert, l'únic operador autoadjunt compacte que té per a espectre {0} és l'operador nul.

• Sigui un operador autoadjunt compacte en un espai Hilbert separable. Llavors existeix una base de hilbert de vectors propis per a l'operador.

Aplicació a la química quàntica

Article principal: Equació de Schrödinger

Òrbites estables d'un electró de l'àtom d'hidrogen.

La teoria espectral constitueix la base matemàtica de la mecànica quàntica. Els vectors propis troben innombrables aplicacions en aquest àmbit. Per exemple en química, l'estudi de l'àtom d'hidrogen mostra que els estats estables dels electrons es modelitzen per vectors propis dels quals els valors propis corresponen a nivells d'energia.

En el context de la mecànica quàntica, l'única solució per descriure la posició d'un electró, en l'exemple de la figura el de l'hidrogen, és la utilització d'una funció d'ona complexa. El quadrat del mòdul d'aquesta funció d'ona es pot interpretar com la probabilitat de presència de l'electró en un punt donat de l'espai. L'espai de les funcions d'ones és un espai Hilbert separable, és l'espai de les funcions del nostre espai geomètric en els complexos tals que el quadrat del seu mòdul és integrable.

L'equació que regeix aquesta funció d'ona (que s'escriu aquí Ψ_E) és una versió simplificada de l'equació de Schrödinger :

$H\Psi _{E}=E\Psi _{E}\;$

H és un operador lineal anomenat hamiltonà. És un operador diferencial d'ordre 2. Correspon a una transformació de Legendre d'un Lagrangià. Es pot demostrar que aquest operador és autoadjunt.

E és un d'escalar, que representa el nivell d'energia de l'electró.

Ψ_E és la incògnita de l'equació. És doncs per definició una funció pròpia, correspon al que els químics diuen una òrbita estable. Els electrons només poden saltar d'una òrbita estable a un altre.

L'equació d'ona que regeix l'electró correspon doncs al marc de la teoria espectral. Les solucions són les funcions pròpies d'un operador lineal. La geometria correspon a un context favorable, l'espai és un espai de Hilbert separable i l'operador és autoadjunt. Se'n pot per exemple deduir directament que l'energia és sempre un nombre real. En canvi les propietats de continuïtat no són favorables. Per exemple, l'operador no és compacte. Aquesta absència de bona continuïtat dificulta la cerca d'òrbites estables.

El cas de l'àtom d'hidrogen és particular. L'operador associat correspon a un cas relativament senzill. En aquest cas les funcions pròpies es poden avaluar amb tanta precisió com es vulgui. La figura representa les primeres òrbites estables de l'àtom d'hidrogen. El color representa el quadrat del mòdul de l'òrbita, com més és clar, més gran és la densitat de la probabilitat de trobar l'electró en el punt. El centre representa el nucli, aquí un protó.

Aquest enfocament no es limita a l'àtom d'hidrogen, se'l pot utilitzar per a altres àtoms i fins i tot molècules. És el treball que realitzà Linus Pauling al seu llibre The Nature of the Chemical Bond sobre la naturalesa dels enllaços químics. El premi Nobel de Química, obtingut principalment gràcies a aquest plantejament és un dels més importants en la química del segle xx. La combinació lineal de les òrbites estables permet per exemple, en el cas de les molècules, descriure millor els compostos insaturats de l'etilè.

Valor propi i recerca matemàtica

Els valors propis continuen sent un vast subjecte de recerca en les matemàtiques d'avui. Aquest subjecte cobreix tan la recerca fonamental com l'aplicada i la dimensió finita com el cas general en dimensió infinita.

Recerca fonamental i dimensió finita

Si bé en el cas dels cossos relativament coneguts com els nombres reals o complexos, la problemàtica dels valors propis és àmpliament coneguda, no n'és igualment per als cossos més esotèrics o quant en comptes de cossos es treballa amb anells. En el cas dels cossos finits, aquest enfocament ofereix una visió particular per exemple sobre la criptografia. Altres cossos com els nombres p-àdics encara són molt poc coneguts. Un enfocament lineal, amb l'anàlisi dels valors propis representa una eina suplementària per a l'anàlisi per exemple de l'anell dels polinomis.

Recerca aplicada i dimensió finita

L'anàlisi dels valors propis i dels vectors propis representa el millor mètode per a la posada a punt d'algorismes ràpids de resolució d'equacions lineals. Criteris com la velocitat de convergència esdevé llavors el principal subjecte de recerca. Una tècnica particularment utilitzada consisteix a allunyar els valors propis per accelerar la cerca de les solucions. Aquest sector, fins i tot si no és dominat per matemàtics en el sentit teòric del terme, ja que és més sovint l'àmbit de les matemàtiques de l'enginyer o de l'informàtic, és sempre en plena efervescència. Uneix els treballs sobre l'anell dels nombres di-àdics (representació binària finita) i s'obre sobre una branca de les matemàtiques difícil.

La criptografia aplicada utilitza també les representacions lineals per oferir codis multiclau eficaços i flexibles. Aquí, els cossos rarament són els reals o els complexos, sinó més aviat cossos finits.

Recerca teòrica en el cas general

Aquest àmbit és el que reuneix més matemàtics teòrics. L'àlgebra lineal és un problema encara àmpliament obert en el cas de la dimensió infinita. La via teòrica més analitzada actualment és la de l'axiomatització, que es materialitza en la geometria algèbrica. Aquest enfocament considera els operadors com a elements d'una àlgebra abstracta, que posseeixen un cert nombre de propietats. L'objectiu és la comprensió d'aquesta àlgebra per aplicar-lo llavors a casos particulars d'àlgebra d'operadors. Aquest enfocament és particularment fecund en matemàtiques aplicades a la física, com per exemple els treballs del matemàtic rus Maksim Kontsévitx (Medalla Fields 1998), se seus resultats més cèlebres tracten de les deformacions quàntiques sobre les Varietats de Poisson amb l'ajuda d'una jerarquia infinita d'estructures algèbriques que generalitzen la noció d'àlgebra que opera sobre un espai vectorial.

La geometria algèbrica és particularment fecunda en l'àmbit de l'aritmètica. El matemàtic Laurent Lafforgue va rebre la Medalla Fields el 2002 pels seus treballs en aquesta branca sobre les conjectures de Langlands.

Bibliografia

• Serge Lang. Algèbre, Dunod.
• Haïm Brezis. Analyse fonctionnelle Théorie et applications, Masson.
• Walter Rudin. Functional analysis, McGraw-Hill Science.
• R. Feynman; R. Leighton; M. Sands. Le cours de physique de Feynmann Vol IV Mécanique quantique, Dunod.
• N. Dunford; J. Schwartz. Linear Operator, General Theory, Wiley-Inerscience.

Enllaços externs

• (francès) "Eléments propres d'un endomorphisme".
• (francès) "Comment fonctionne Google?" Arxivat 2009-04-19 a Wayback Machine., utilització i càlcul de vectors propis en l'algoritme PageRank.  PDF