Distribució khi
Funció de densitat de probabilitat  | |
Funció de distribució de probabilitat 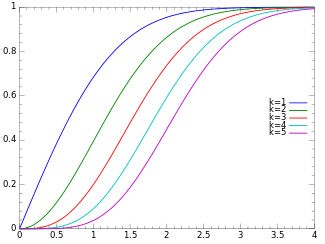 | |
| Paràmetres | (graus de llibertat) |
|---|---|
| Suport | |
| fdp | |
| FD | |
| Esperança matemàtica | |
| Mediana | |
| Moda | per a |
| Variància | |
| Coeficient de simetria | |
| Curtosi | |
| Entropia | |
| FGM | Complex (vegeu text) |
| FC | Complex (vegeu text) |
En teoria i estadística de probabilitats, la distribució khi és una distribució de probabilitat contínua. És la distribució de l'arrel quadrada positiva de la suma de quadrats d'un conjunt de variables aleatòries independents cadascuna seguint una distribució normal estàndard, o equivalent, la distribució de la distància euclidiana de les variables aleatòries des de l'origen. Per tant, es relaciona amb la distribució khi quadrat descrivint la distribució de les arrels quadrades positives d'una variable que obeeix a una distribució khi quadrat.[1]
Si són variables aleatòries independents, distribuïdes normalment amb mitjana 0 i desviació estàndard 1, aleshores l'estadística
es distribueix segons la distribució de khi. La distribució de khi té un paràmetre, , que especifica el nombre de graus de llibertat (és a dir, el nombre de variables aleatòries ).
Els exemples més coneguts són la distribució de Rayleigh (distribució de khi amb dos graus de llibertat) i la distribució de Maxwell-Boltzmann de les velocitats moleculars en un gas ideal (distribució de khi amb tres graus de llibertat).[2]
Funció de densitat de probabilitat
[modifica]La funció de densitat de probabilitat (pdf) de la distribució khi és
on és la funció gamma.
Funció de distribució acumulada
[modifica]La funció de distribució acumulada ve donada per:
on P(k,x) és la funció gamma regularitzada.[4]
Referències
[modifica]- ↑ «15.8 - Chi-Square Distributions | STAT 414» (en anglès). https://online.stat.psu.edu.+[Consulta: 1r juliol 2023].
- ↑ «1.3.6.6.6. Chi-Square Distribution» (en anglès). https://www.itl.nist.gov.+[Consulta: 1r juliol 2023].
- ↑ Weisstein, Eric W. «Chi Distribution» (en anglès). https://mathworld.wolfram.com.+[Consulta: 1r juliol 2023].
- ↑ «Chi-square distribution | Mean, variance, proofs, exercises» (en anglès). https://www.statlect.com.+[Consulta: 1r juliol 2023].




















