 Distribució t de Student
Distribució t de Student |
Funció de distribució de probabilitat  |
| Tipus | Distribució t multivariant, Distribució t no central, família escala de localització, distribució de probabilitat simètrica, distribució univariant i distribució de probabilitat contínua  |
|---|
| Epònim | William Gosset  |
|---|
| Paràmetres |  graus de llibertat graus de llibertat |
|---|
| Suport |  |
|---|
| FD | ![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\times \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c3c84e8f1257dce799724d08e3b08389944045d)
on ₂F1 és la funció hipergeomètrica |
|---|
| Esperança matemàtica | 0 per a  |
|---|
| Mediana | 0 |
|---|
| Moda | 0 |
|---|
| Variància |  per a per a  |
|---|
| Coeficient de simetria | 0 per a  |
|---|
| Curtosi |  per a per a  |
|---|
| Entropia | ![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi \left({\frac {1+\nu }{2}}\right)-\psi \left({\frac {\nu }{2}}\right)\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B\left({\frac {\nu }{2}},{\frac {1}{2}}\right)\right]}\,{\scriptstyle {\text{(nats)}}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e64e6a7fd1bb08a7129701a00f10b4dc673c589)
on ψ és la funció digamma i B és la funció beta |
|---|
| FGM | cap valor  |
|---|
| FC |  on
on  és Funció de Bessel modificada de segon tipus és Funció de Bessel modificada de segon tipus |
|---|
| Mathworld | Studentst-Distribution  |
|---|
En probabilitat i estadística, la distribució t de Student és una distribució de probabilitat que sorgeix del problema d'estimar la mitjana d'una població normalment distribuïda amb variància desconeguda quan la mida de la mostra és petita. Aquesta és la base de la popular prova t de Student per a la determinació de les diferències entre dues mitjanes mostrals i per a la construcció de l'interval de confiança per a la diferència entre les mitjanes de dues poblacions.
El seu nom, Student, es deu al pseudònim que utilitzava l'estadístic britànic William Sealey Gosset quan publicava els seus articles científics. Per a la història d'aquesta distribució vegeu la pàgina Prova t de student.
La referència bàsica d'aquest article és Johnson et al..
Sigui  una variable aleatòria normal estàndard i
una variable aleatòria normal estàndard i  una variable aleatòria amb distribució
una variable aleatòria amb distribució  amb
amb  graus de llibertat,
graus de llibertat,  i
i  independents. La variable
independents. La variable  es diu que té una distribució
es diu que té una distribució  de Student amb
de Student amb  graus de llibertat i s'escriu
graus de llibertat i s'escriu  o bé
o bé  .
.
Comentari sobre els graus de llibertat. El cas més habitual d'una distribució  és quan el nombre
és quan el nombre  de graus de llibertat és un nombre natural i llavors es pot interpretar com la suma dels quadrats de
de graus de llibertat és un nombre natural i llavors es pot interpretar com la suma dels quadrats de  variables aleatòries normals estàndard independents. Però mitjançant la funció de densitat es pot definir una distribució
variables aleatòries normals estàndard independents. Però mitjançant la funció de densitat es pot definir una distribució  que tingui com a graus de llibertat qualsevol nombre real estrictament positiu
que tingui com a graus de llibertat qualsevol nombre real estrictament positiu  , nombre que continua anomenat-se els graus de llibertat de la distribució.[2] En conseqüència, pot definir-se la distribució
, nombre que continua anomenat-se els graus de llibertat de la distribució.[2] En conseqüència, pot definir-se la distribució  de Student amb graus de llibertat qualsevol nombre
de Student amb graus de llibertat qualsevol nombre  . Cal dir que el programari estadístic estàndard, per exemple, el llenguatge R, utilitza graus de llibertat fraccionaris en certs tests estadístics.
. Cal dir que el programari estadístic estàndard, per exemple, el llenguatge R, utilitza graus de llibertat fraccionaris en certs tests estadístics.
La funció de densitat de la distribució  de Student amb
de Student amb  graus de llibertat és
graus de llibertat és
|

|
on  és la funció gamma.
és la funció gamma.
Utilitzant la funció Beta  i que
i que  també es pot escriure
també es pot escriure  Funció parella. Cal remarcar que aquesta funció és parella :
Funció parella. Cal remarcar que aquesta funció és parella :  ; gràficament, és simètrica respecte l'eix d'ordenades. Aquesta propietat és important en els càlculs de probabilitats.
; gràficament, és simètrica respecte l'eix d'ordenades. Aquesta propietat és important en els càlculs de probabilitats.
Prova
El càlcul de la funció de densitat de

es fa mitjançant la fórmula de canvi de variables per a
vectors aleatoris. Concretament, amb les notacions que hem introduït a la definició de

, considerem la funció

que transforma el vector

en el vector

:

La transformació inversa és

El determinant jacobià d'aquesta transformació és  D'altra banda, degut a que
D'altra banda, degut a que  i
i  són independents, la densitat conjunta del vector
són independents, la densitat conjunta del vector és el producte de les funcions de densitat:
és el producte de les funcions de densitat: 
Llavors, la densitat conjunta de

és

La densitat (marginal) de

és

on, per calcular la integral, hem fet el canvi de variable

i hem utilitzat la
funció gamma.
Quan  és un nombre natural, la funció de densitat és simplifica. Concretament,per a
és un nombre natural, la funció de densitat és simplifica. Concretament,per a  ,
,  Llavors
Llavors  i per tant es tracta d'una distribució de Cauchy (centrada en l'origen).
Per a
i per tant es tracta d'una distribució de Cauchy (centrada en l'origen).
Per a  senar, la constant de la funció de densitat és
senar, la constant de la funció de densitat és  on
on  és el doble factorial del nombre
és el doble factorial del nombre  .
.
Per a  parell,
parell,  (Cal recordar que
(Cal recordar que  =1).
=1).
Quan el nombre de graus de llibertat és un nombre natural, la funció de distribució es pot donar explícitament en termes de funcions elementals, amb una expressió que es complica a l'augmentar els graus de llibertat.

|
Funció de densitat
|
Funció de distribució
|
| 1
|

|

|
| 2
|

|

|
| 3
|

|
![{\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {1}{\sqrt {3}}}{\frac {t}{1+{\frac {t^{2}}{3}}}}+\arctan \left({\frac {t}{\sqrt {3}}}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0afffc07f0c86a59eaa560dc8a3cf8f6fa83ccd)
|
| 4
|

|
![{\displaystyle {\frac {1}{2}}+{\frac {3}{8}}{\frac {t}{\sqrt {1+{\frac {t^{2}}{4}}}}}{\left[1-{\frac {1}{12}}{\frac {t^{2}}{1+{\frac {t^{2}}{4}}}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8267697404a72109b22e9add73ef7023d1953235)
|
| 5
|

|
![{\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {t}{{\sqrt {5}}\left(1+{\frac {t^{2}}{5}}\right)}}\left(1+{\frac {2}{3\left(1+{\frac {t^{2}}{5}}\right)}}\right)+\arctan \left({\frac {t}{\sqrt {5}}}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeef99bb2df092bdcc8c708cbc0c29cfe1849232)
|
Prova
El càlcul de la funció de distribució es redueix a calcular una integral de la forma

, amb

i

o

amb

i

un nombre senar. En ambdós casos, mitjançant el canvi

n'hi ha prou amb considerar

.
Tenim que

i per a  , la integral
, la integral  és una integral d'una funció racional amb arrels complexes múltiples, que dona[3]
és una integral d'una funció racional amb arrels complexes múltiples, que dona[3]  La integral
La integral  per a
per a  senar, mitjançant el canvi
senar, mitjançant el canvi  es converteix en una integral de la forma
es converteix en una integral de la forma  , que es pot calcular iterativament (vegeu la fórmula de la integral d'una potència del cosinus), i acaba donant:[3]
, que es pot calcular iterativament (vegeu la fórmula de la integral d'una potència del cosinus), i acaba donant:[3] 
Calculem, per exemple, la funció de distribució per a  : hem de calcular
: hem de calcular 
Llavors,

Expressions alternatives de la funció de distribució
[modifica]Per al cas general podem escriure la funció de distribució en termes de la funció beta incompleta:
 on
on  i
i  és la funció beta incompleta regularitzada.
és la funció beta incompleta regularitzada.
Per a  , atès que la funció de densitat és parella, el càlcul de
, atès que la funció de densitat és parella, el càlcul de  és fa per arguments de simetria.
és fa per arguments de simetria.
Prova
Fixat

, tenim que

on hem utilitzat la simetria respecte l'eix d'ordenades de la funció de densitat

. A la darrera integral fem el canvi

amb la qual cosa aquesta integral queda

on

és la funció Beta i és la funció Beta incompleta regularitzada

. D'on es dedueix la fórmula per a

.
També, per a  , es pot escriure la funció de distribució en termes d'una funció hipergeomètrica
, es pot escriure la funció de distribució en termes d'una funció hipergeomètrica
 on
on  és una funció hipergeomètrica.
és una funció hipergeomètrica.
Sigui  un nombre natural. Aleshores
un nombre natural. Aleshores
- Si
 , tenim que
, tenim que ![{\displaystyle E[T^{n}]={\begin{cases}0,&{\text{si}}\ n\ {\text{és senar}},\\\\\nu ^{n/2}\,{\dfrac {\Gamma {\big (}{\frac {n+1}{2}}{\big )}\,\Gamma {\big (}{\frac {\nu -n}{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2}}{\big )}\Gamma {\big (}{\frac {\nu }{2}}{\big )}}},&{\text{si}}\ n\ {\text{és parell}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02a293e71c63f0843b6e2eb49dca5bd992cfdaa)
- Si
 , llavors
, llavors ![{\displaystyle E{\big [}\vert T^{n}\vert {\big ]}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e1e06f572bfb47911ab07c88be48f3e4ee2de7) , i en conseqüència el moment d'ordre
, i en conseqüència el moment d'ordre  no existeix.
no existeix.
En el cas  parell,
parell,  , també tenim
, també tenim ![{\displaystyle E[T^{n}]=\nu ^{n/2}\,{\frac {1\cdot 3\cdots (n-1)}{(\nu -n)(\nu -n+2)\cdots (\nu -2)}}=\nu ^{n/2}\,\prod _{i=1}^{n/2}{\frac {2i-1}{\nu -2i}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/265816dfc1e5f302cd3ee717d69ffaa78da68290)
En particular, si  , llavors
, llavors ![{\displaystyle E[T]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06bb980f5db991d84b0228e6d7834cfa202cd1ae) . Si
. Si  , llavors
, llavors ![{\displaystyle {\text{Var}}(T)=E[T^{2}]={\frac {\nu }{\nu -2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a82ba7c78e0b44433984bc600f5f31bfee46608d)
Prova
El càlcul dels moments és senzill a partir de la definició de la variable

. Comencem estudiant quan existeixen els moments de

. D'acord amb la seva definició i les notacions que hem introduït,
![{\displaystyle E{\big [}\vert T\vert ^{n}{\big ]}=\nu ^{n/2}\,E{\big [}\vert Z\vert ^{n}{\big ]}\,E{\big [}Q^{-n/2}{\big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a94501f770219bff11963f02b646cf2e73e3113)
on hem utilitzat que

i

són independents i positives. Atès que una
variable normal té moments de tots els ordres, l'expressió anterior serà finita o no segons ho sigui
![{\displaystyle E[Q^{-n/2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca13a41b68cafc3b44518e406f3548732b650304)
. Tenim que
![{\displaystyle E{\big [}Q^{-n/2}{\big ]}={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{-n/2}x^{(\nu /2)-1}e^{-x/2}\,dx={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{(\nu -n)/2-1}e^{-x/2}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6663587fd922ea8575e384d308de84fb26272e57) Fen el canvi
Fen el canvi  , la integral de la dreta dona
, la integral de la dreta dona  quan
quan  , i
, i  en cas contrari.
en cas contrari.
Ara, per calcular els moments quan  , és a dir, si
, és a dir, si  , repetim els càlculs anteriors sense el valor absolut tenint en compte que per a una variable normal estàndard tenim
, repetim els càlculs anteriors sense el valor absolut tenint en compte que per a una variable normal estàndard tenim![{\displaystyle E[Z^{n}]={\begin{cases}0,&{\text{si}}\ n\ {\text{és senar}},\\\\{\dfrac {2^{n/2}}{\sqrt {\pi }}}\,\Gamma {\big (}{\frac {n+1}{2}}{\big )},&n\ {\text{és parell}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367cb85fa98d887a40ecbfdf33137bc1321bf68b) D'on
D'on
![{\displaystyle E[T^{n}]=\nu ^{n/2}\,{\dfrac {\Gamma {\big (}{\frac {n+1}{2}}{\big )}\,\Gamma {\big (}{\frac {\nu -n}{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2}}{\big )}\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e72e3721fa66632d0169b4dd4cd4eee51e481e2)
Sigui  , aleshores per a
, aleshores per a  gran,
gran,  és aproximadament normal estàndard
és aproximadament normal estàndard  .
.
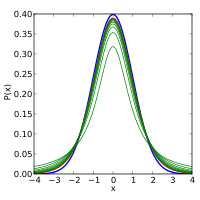
Els següents gràfics mostren la densitat de la distribució  per a valors creixents de
per a valors creixents de  . La densitat de la distribució normal estàndard està dibuixada en blau. Noteu que la densitat de la distribució
. La densitat de la distribució normal estàndard està dibuixada en blau. Noteu que la densitat de la distribució  (en vermell) s'aproxima cada com més a la normal quan
(en vermell) s'aproxima cada com més a la normal quan  creix.
creix.
Prova
Designem per

la funció de densitat de la distribució

,

aplicant les propietats asimptòtiques de la
funció gamma i calculant un límit del nombre

, es demostrar que

d'on, per les propietats de la
convergència en distribució, s'obté també l'aproximació normal a la distribució

.
Quan el nombre de graus de llibertat és una nombre natural, hi ha fórmules per la funció característica de la distribució de Student, que depenen de si els graus de llibertat son senars o parells, fórmules que cada cop són més complicades a l'augmentar el nombre de graus de llibertat. Una fórmula general utilitzant funcions especials va ser obtinguda el 1995 independentment per S. Hurst [8] i A. H. Jorder (veieu).[9] Concretament, si  ,
,![{\displaystyle \varphi (t)=E[e^{itT}]={\frac {K_{\nu /2}\left({\sqrt {\nu }}|t|\right)\,\left({\sqrt {\nu }}|t|\right)^{\nu /2}}{\Gamma (\nu /2)\,2^{\nu /2-1}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1954c22dda6c042394c66102826a8ed8dd725cde) on
on  és la funció de Bessel modificada de segon tipus.
és la funció de Bessel modificada de segon tipus.
La distribució t de Student amb tres paràmetres
[modifica]La funció de densitat  d'una distribució
d'una distribució  permet construir de la manera habitual una família de posició i escala :[10] sigui
permet construir de la manera habitual una família de posició i escala :[10] sigui  i
i  ; definim
; definim  Aquesta distribució s'anomena distribució
Aquesta distribució s'anomena distribució  de Student amb tres paràmetres, o distribució
de Student amb tres paràmetres, o distribució  de Student amb posició i escala, i es designa per
de Student amb posició i escala, i es designa per  o
o  . Alternativament, si
. Alternativament, si  , llavors la variable aleatòria
, llavors la variable aleatòria 
té distribució  .
.
La distribució t de Student en Estadística
[modifica]El paper central que té distribució  de Student en la inferència estadística de poblacions normals és degut al següent teorema:[11]
de Student en la inferència estadística de poblacions normals és degut al següent teorema:[11]
Teorema. Sigui  una mostra d'una població normal una mostra d'una població normal  , és a dir, les variables aleatòries , és a dir, les variables aleatòries  són independents i totes tenen distribució són independents i totes tenen distribució  . Considerem la mitjana mostral . Considerem la mitjana mostral  Aleshores: Aleshores:
 - Les variables aleatòries
 i i  són independents. són independents.
- Sigui

on  és la variància mostral. Llavors, és la variància mostral. Llavors,  . .
|
Vegeu la pàgina de la distribució  per a la demostració dels punts 1 i 2. El punt 3 es dedueix del fet que
per a la demostració dels punts 1 i 2. El punt 3 es dedueix del fet que  i de les parts 1 i 2 i de la definició de la distribució
i de les parts 1 i 2 i de la definició de la distribució  de Student.
de Student.
Vegeu la pàgina Interval de confiança per a exemples concrets d'utilització de la distribució de Student.
Relació amb altres distribucions
[modifica]- La distribució
 coincideix amb la distribució de Cauchy.
coincideix amb la distribució de Cauchy.
- Si
 , aleshores
, aleshores  té una distribució
té una distribució  amb 1 i
amb 1 i  graus de llibertat:
graus de llibertat:  .
.
- ↑ Johnson, N. L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 1. 2a edició. Nova York: Wiley, 1994, p. 417. ISBN 0-471-58495-9.
- ↑ 3,0 3,1 Gradshteĭn, I. S.. Table of integrals, series and products. 7th ed. Oxford: Academic, 2007, p. 96, fórmula 2.263.3. ISBN 978-0-12-373637-6.
- ↑ Hurst, Simon. [url=https://web.archive.org/web/20100218072259/http://wwwmaths.anu.edu.au/research.reports/srr/95/044/ The Characteristic Function of the Student-t Distribution], Financial Mathematics Research Report No. FMRR006-95, Statistics Research Report No. SRR044-95
- ↑ Gaunt, Robert E. «A simple proof of the characteristic function of Student’s t -distribution» (en anglès). Communications in Statistics - Theory and Methods, 50, 14, 18-07-2021, pàg. 3380–3383. DOI: 10.1080/03610926.2019.1702695. ISSN: 0361-0926.
- ↑ Casella, George; Berger, Roger L. Statistical inference. 2. ed. Pacific Grove, Calif: Duxbury, 2002, p. 119. ISBN 978-0-534-24312-8.
- ↑ DeGroot, Morris H. Probabilidad y estadística. 2a. ed. Wilmington, Delawere, E.U.A.: Addison-Wesley Iberoamericaca, 1988, p. 373-374 i 379-380. ISBN 0-201-64405-3.
- Johnson, N. L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2. 2a edició. Nova York: Wiley, 1995. ISBN 0-471-58494-0.
|
|---|
|
Distribucions discretes
amb suport finit | |
|---|
Distribucions discretes
amb suport infinit | |
|---|
Distribucions contínues
suportades sobre un interval acotat | |
|---|
Distribucions contínues
suportades sobre un interval semi-infinit | |
|---|
Distribucions contínues
suportades en tota la recta real | |
|---|
Distribucions contínues
amb el suport de varis tipus | |
|---|
| Barreja de distribució variable-contínua | |
|---|
| Distribució conjunta | |
|---|
| Direccionals | |
|---|
| Degenerada i singular | |
|---|
| Famílies | |
|---|





![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\times \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c3c84e8f1257dce799724d08e3b08389944045d)






![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi \left({\frac {1+\nu }{2}}\right)-\psi \left({\frac {\nu }{2}}\right)\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B\left({\frac {\nu }{2}},{\frac {1}{2}}\right)\right]}\,{\scriptstyle {\text{(nats)}}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e64e6a7fd1bb08a7129701a00f10b4dc673c589)












































![{\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {1}{\sqrt {3}}}{\frac {t}{1+{\frac {t^{2}}{3}}}}+\arctan \left({\frac {t}{\sqrt {3}}}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0afffc07f0c86a59eaa560dc8a3cf8f6fa83ccd)

![{\displaystyle {\frac {1}{2}}+{\frac {3}{8}}{\frac {t}{\sqrt {1+{\frac {t^{2}}{4}}}}}{\left[1-{\frac {1}{12}}{\frac {t^{2}}{1+{\frac {t^{2}}{4}}}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8267697404a72109b22e9add73ef7023d1953235)

![{\displaystyle {\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {t}{{\sqrt {5}}\left(1+{\frac {t^{2}}{5}}\right)}}\left(1+{\frac {2}{3\left(1+{\frac {t^{2}}{5}}\right)}}\right)+\arctan \left({\frac {t}{\sqrt {5}}}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeef99bb2df092bdcc8c708cbc0c29cfe1849232)


































![{\displaystyle E[T^{n}]={\begin{cases}0,&{\text{si}}\ n\ {\text{és senar}},\\\\\nu ^{n/2}\,{\dfrac {\Gamma {\big (}{\frac {n+1}{2}}{\big )}\,\Gamma {\big (}{\frac {\nu -n}{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2}}{\big )}\Gamma {\big (}{\frac {\nu }{2}}{\big )}}},&{\text{si}}\ n\ {\text{és parell}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02a293e71c63f0843b6e2eb49dca5bd992cfdaa)

![{\displaystyle E{\big [}\vert T^{n}\vert {\big ]}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e1e06f572bfb47911ab07c88be48f3e4ee2de7)

![{\displaystyle E[T^{n}]=\nu ^{n/2}\,{\frac {1\cdot 3\cdots (n-1)}{(\nu -n)(\nu -n+2)\cdots (\nu -2)}}=\nu ^{n/2}\,\prod _{i=1}^{n/2}{\frac {2i-1}{\nu -2i}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/265816dfc1e5f302cd3ee717d69ffaa78da68290)
![{\displaystyle E[T]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06bb980f5db991d84b0228e6d7834cfa202cd1ae)
![{\displaystyle {\text{Var}}(T)=E[T^{2}]={\frac {\nu }{\nu -2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a82ba7c78e0b44433984bc600f5f31bfee46608d)
![{\displaystyle E{\big [}\vert T\vert ^{n}{\big ]}=\nu ^{n/2}\,E{\big [}\vert Z\vert ^{n}{\big ]}\,E{\big [}Q^{-n/2}{\big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a94501f770219bff11963f02b646cf2e73e3113)

![{\displaystyle E[Q^{-n/2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca13a41b68cafc3b44518e406f3548732b650304)
![{\displaystyle E{\big [}Q^{-n/2}{\big ]}={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{-n/2}x^{(\nu /2)-1}e^{-x/2}\,dx={\frac {1}{2^{\nu /2}\Gamma (\nu /2)}}\int _{0}^{\infty }x^{(\nu -n)/2-1}e^{-x/2}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6663587fd922ea8575e384d308de84fb26272e57)





![{\displaystyle E[Z^{n}]={\begin{cases}0,&{\text{si}}\ n\ {\text{és senar}},\\\\{\dfrac {2^{n/2}}{\sqrt {\pi }}}\,\Gamma {\big (}{\frac {n+1}{2}}{\big )},&n\ {\text{és parell}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367cb85fa98d887a40ecbfdf33137bc1321bf68b)
![{\displaystyle E[T^{n}]=\nu ^{n/2}\,{\dfrac {\Gamma {\big (}{\frac {n+1}{2}}{\big )}\,\Gamma {\big (}{\frac {\nu -n}{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2}}{\big )}\Gamma {\big (}{\frac {\nu }{2}}{\big )}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e72e3721fa66632d0169b4dd4cd4eee51e481e2)














![{\displaystyle \varphi (t)=E[e^{itT}]={\frac {K_{\nu /2}\left({\sqrt {\nu }}|t|\right)\,\left({\sqrt {\nu }}|t|\right)^{\nu /2}}{\Gamma (\nu /2)\,2^{\nu /2-1}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1954c22dda6c042394c66102826a8ed8dd725cde)






















