Distribució de Bates

Distribució de Bates

Funció de densitat de probabilitat 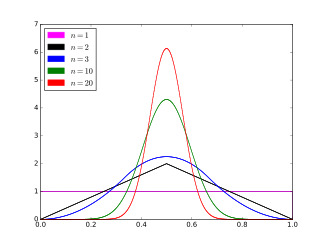Cas $a=0,\ b=1$
Funció de distribució de probabilitat 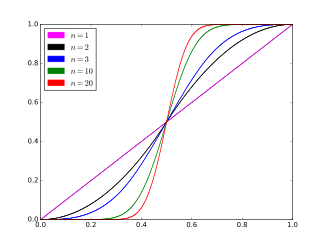Cas $a=0,\ b=1$
Tipus	distribució de probabilitat i distribució de probabilitat simètrica
Epònim	Grace Bates
Paràmetres	$-\infty <a<b<\infty$ $n\geq 1$ nombre natural
Suport	$x\in [a,b]$
fdp	vegeu text
Esperança matemàtica	${\tfrac {1}{2}}(a+b)$
Variància	${\tfrac {1}{12n}}(b-a)^{2}$
Coeficient de simetria	$0$
Curtosi	$-{\tfrac {6}{5n}}$
FC	$\left(-{\frac {in(e^{\tfrac {ibt}{n}}-e^{\tfrac {iat}{n}})}{(b-a)t}}\right)^{n}$

En teoria de la probabilitat i estadística, la distribució de Bates, que duu el nom de Grace E. Bates, és la distribució de probabilitat de la mitjana de n variables aleatòries independents, cadascuna amb distribució uniforme en l'interval unitat [0,1]. Aquesta distribució està relacionada amb la distribució d'Irwin–Hall, que és la distribució de la suma de n variables aleatòries independents amb distribució uniforme a l'interval [0,1], i, a vegades, es confonen ambdues. Malgrat els noms de Bates, Irwing i Hall, aquesta mena de distribucions van ser estudiades per Joseph Luis Lagrange el 1770 i per Nicolai Lobatxevski el 1832, i redescobertes per nombrosos autors.

Definició i funció de densitat

Siguin $U_{1},\dots ,U_{n}$ variables aleatòries independents, totes amb distribució uniforme en l'interval [0,1]. Designem per $M_{n}$ la mitjana d'aquestes variables: $$M_{n}={\frac {1}{n}}\sum _{j=1}^{n}U_{j}.$$ La distribució de $M_{n}$ és coneguda com a distribució de Bates. És una distribució contínua amb funció de densitat$$f_{M_{n}}(x)={\begin{cases}{\dfrac {n^{n}}{(n-1)^{n}}}\displaystyle {\sum _{k=0}^{[nx]}}(-1)^{k}{\dbinom {n}{k}}{\Big (}x-{\dfrac {k}{n}}{\Big )}^{n-1},&\ {\text{si}}\ x\in [0,1],\\\\0,&{\text{en cas contrari}},\end{cases}}$$on $[r]$ és la part entera del nombre real $r$ .

Alternativament $$f_{M_{n}}(x)={\frac {n^{n}}{(n-1)^{n}}}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}{\Big (}x-{\frac {k}{n}}{\Big )}_{+}^{n-1},\ x\in [0,1],$$on $$r_{+}^{m}={\begin{cases}r^{m},&{\text{si}}\ r>0\\0,&{\text{en cas contrari}}.\end{cases}}$$Ambdues expressions són equivalents, ja que a la segona expressió, per a $j=[nx]+1,\dots ,n$, tenim que $x-j/n<0$.

Sigui $S_{n}$ la suma de $U_{1},\dots ,U_{n}$ : $$S_{n}=\sum _{j=1}^{n}U_{j},$$ que té una distribució d'Irwin-Hall, i designem per $f_{S_{n}}(x)$ la seva funció de densitat. Tenim que $$M_{n}={\frac {1}{n}}\,S_{n}.$$Per la fórmula de canvi de variables per a variables aleatòries amb densitat tenim que $$f_{M_{n}}(x)=n\,f_{S_{n}}(nx).$$Per tant, la fórmula de $f_{M_{n}}(x)$ es dedueix de la $f_{S_{n}}(x)$ a la pagina de la distribució d'Irwin-Hall on també hi ha les demostracions corresponents.

Totes les propietats de la distribució de Bates (moments, funció característica,....) es dedueixen de les corresponents propietats de les distribucions uniformes i de la independència de $U_{1},\dots ,U_{n}$.

Generalització

Com a la secció anterior, designem per $f_{M_{n}}(x)$ la funció de densitat de Bates

Siguin $V_{1},\dots ,V_{n}$ variables aleatòries independents, amb distribució uniforme en l'interval $[a,b]$, amb $a<b$, sigui $f_{M_{n}}(x;a,b)$ la funció de densitat de la mitjana ${\frac {1}{n}}\sum _{j=1}^{n}V_{n}$ aleshores $$f_{M_{n}}(x;a,b)={\frac {1}{b-a}}\,f_{M_{n}}{\Big (}{\frac {x-a}{b-a}}{\Big )},\ x\in [a,b].$$

Aproximació normal

Tal com mostra el gràfic del principi de la pàgina, a l'augmentar $n$, la distribució de Bates s'assembla cada cop més a una distribució normal. Això és degut al fet que podem aplicar el teorema central del límit. Concretament, considerem el cas general que hem considerat a l'apartat anterior amb $V_{1},\dots ,V_{n}$ amb distribució uniforme en l'interval $[a,b]$, i $$M_{n}={\frac {1}{n}}\sum _{j=1}^{n}V_{j}\quad {\text{i}}\quad S_{n}=\sum _{j=1}^{n}V_{j}.$$Atès que $$E[V_{j}]={\frac {a+b}{2}}\quad {\text{i}}\quad {\text{Var}}(V_{j})={\frac {(b-a)^{2}}{12}},$$tindrem que $$\lim _{n\to \infty }{\sqrt {12n}}\,\,{\frac {M_{n}-(a+b)/2}{b-a}}=Z,\ {\text{en distribució}},$$on $Z$ te una distribució normal estàndard ${\mathcal {N}}(0,1)$ . També es diu que $M_{n}$ és asimptòticament normal amb mitjana $(a+b)/2$ i variància $(b-a)^{2}/(12n)$ : $$M_{n}\sim {\mathcal {AN}}{\bigg (}{\frac {a+b}{2}},{\frac {(b-a)^{2}}{12n}}{\bigg )}.$$

El cas de Lobatxevski

Lobatxevski considera el cas $b=1$ i $a=-1$ , és a dir, les variables de partida tenen distribució uniforme a l'interval $[-1,1]$, que interpreta com els errors en prendre mesures repetides de determinada quantitat (en unes unitats no especificades). Llavors la densitat de la seva mitjana és$$f_{M_{n}}(x;-1,1)={\frac {n}{2^{n}(n-1)!}}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}{\Big (}nx+n-2k{\Big )}_{+}^{n-1},\ x\in [-1,1].$$ Vegeu Renyi per a l'expressió de la densitat de la suma de variables independents uniformes en [-1,1].

D'acord amb Maistrov , Lobatxevski tenia interès en aquesta distribució perquè volia estimar, tenint en compte els errors de mesura, si la suma dels angles d'un gran triangle astronòmic era menor que $180^{\circ }$, amb la qual cosa es tindria una prova que la geometria de l'univers era no euclidiana hiperbòlica. Vegeu Brylevskaya.

Vegeu també

• Distribució d'Irwin-Hall
• Distribució normal
• Teorema del límit central
• Distribució uniforme contínua

Bibliografia

• Johnson, N. L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2. 2a edició. Nova York: Wiley, 1995. ISBN 0-471-58494-0.